|
|
||
Известно и описано очень большое количество самых разнообразных многогранников. Видимо поэтому существует также и сравнительно большое количество их определений. Наиболее известные и соответственно часто используемые из них:
"Многогранник можно определить как множество многоугольников, ограничивающих часть трёхмерного пространства".
"Многогранником называется тело, граница которого является объединением конечного числа многоугольников".
"Многогранник, часть пространства, ограниченная совокупностью конечного числа плоских многоугольников, соединенных таким образом, что каждая сторона любого многоугольника является стороной ровно одного другого многоугольника (называемого смежным), причем вокруг каждой вершины существует ровно один цикл многоугольников. Эти многоугольники называются гранями, их стороны - ребрами, а вершины - вершинами многогранника".
"Многогранник - совокупность конечного числа плоских многоугольников такая, что:
- каждая сторона любого из многоугольников есть одновременно сторона другого (но только одного (называемого смежным с первым) по этой стороне);
- от любого из многоугольников составляющих многогранник, можно дойти до любого из них, переходя к смежному с ним, а от этого, в свою очередь, к смежному с ним и т.д.
Эти многоугольники называются гранями, их стороны - ребрами, а их вершины - вершинами многогранника".
Очевидно, что уже первое из приведенных определений является достаточным для однозначного выделения любого многогранника. Однако в различные варианты определений упорно добавляют уточняющие ограничения. Зачем?
Для получения ответа на этот вопрос нужно внимательно рассмотреть уточнения.
И так, первое: число, ограничивающих пространство многоугольников, обязательно должно быть конечным. На первой взгляд это ограничение введено для того, чтобы избежать появления бесконечно больших многогранников или многогранников существующих лишь потенциально, но это не так. Во-первых, в математике используется очень много идеализированных потенциально существующих объектов. Поэтому одним больше, одним меньше - ситуация принципиально не изменится. Во-вторых, не наложены никакие ограничения на размеры, ограничивающих пространство, многоугольников, а это означает, что эти размеры могут быть бесконечно большими. И, тогда, многогранник будет тоже бесконечно большим при конечном числе, ограничивающих его многоугольников.
Тогда получается, это ограничение потребовалось совсем для других целей. Хотя об этом не принято говорить, но дело здесь заключается в том, что при бесконечно большом количестве многоугольников (граней), многогранник становится неотличим, например, от шара. Почему, например? Да, потому, что существуют еще цилиндры, конусы, эллипсоиды, тор и прочие объекты с так называемыми криволинейными поверхностями. От, которых при определенных деформациях многогранник с бесконечно большим количеством граней тоже будет неотличим. Об этом я уже писал и приводил соответствующие примеры (см. статью: "Уравнение многогранников" http://stob2.narod.ru/29s.htm).
После сказанного становится понятным, что главной целью требования, конечности числа граней в многограннике является желание отличить друг от друга многогранник и шар или любой другой объект с криволинейной поверхностью. Видимо, когда-то, кто-то посчитал, что проще согласно определению исключить из состава многогранников многогранники с бесконечным количеством граней, чем объяснять, чем же они отличаются от шаров.
Однако подобные манипуляции будут нормально срабатывать лишь до тех пор пока многогранники будут интересовать в основном, как особо красивые, совершенные и гармоничные геометрические фигуры. И только. Ведь запрет на существование многогранников с бесконечно большим числом граней абсолютно ничем не обоснован. Да, и практическая неразличимость многогранника и шара наступает вовсе не при бесконечно большом количестве граней у многогранника. Она наступает уже при нескольких тысячах граней. Это хорошо видно на Рис. 1. Если же исходить из позиций топологии, так шар и многогранник с любым, даже самым минимальным количеством граней, и вовсе неразличимы.
На Рис. 1 показана анимация постепенного увеличения числа граней у многогранника, начиная с треугольной призмы. И с какого-то момента многогранник начинает однозначно восприниматься, как шар.
Особо необходимо отметить, что все многогранники в анимации на Рис. 1 были построены при помощи системы уравнений (1) из статьи: "Уравнение многогранников" http://stob2.narod.ru/29s.htm. Это важно, но об этом чуть ниже еще будет сказано.
![[]](/img/b/below_a_m/ab21/1.jpg)
где F - угол сферических координат в горизонтальной плоскости; Q - угол сферических координат в вертикальной плоскости; L1 - коэффициент, может быть любым числом, физически представляет собой радиус вписанной в многогранник сферы (эллипсоида в проекции на горизонтальную плоскость); L2 - коэффициент, может быть любым числом, физически представляет собой радиус вписанной в многогранник сферы (эллипсоида в проекции на вертикальную плоскость); N1 - коэффициент, может быть любым числом, от его значения зависит вид, количество сторон (углов) многогранника в проекции на горизонтальную плоскость; N2 - коэффициент, может быть любым числом, от его значения зависит вид, количество сторон (углов) многогранника в проекции на вертикальную плоскость; π - число пи, равное 3,14159...; [ ] - знак, обозначающий целую часть числа и предусматривающий отбрасывание дробной части от результата вычисления выражения, стоящего в скобках [ ]
Рис. 1 Анимация постепенного увеличения числа граней у многогранника, начиная с треугольной призмы до состояния перехода многогранника в шар
Второе ограничение, накладываемое на многогранники, связано со следующей группой уточнений:
- каждая сторона любого многоугольника (в многограннике) является стороной ровно одного другого многоугольника (называемого смежным), причем вокруг каждой вершины существует ровно один цикл многоугольников;
- от любого из многоугольников составляющих многогранник, можно дойти до любого из них, переходя к смежному с ним, а от этого, в свою очередь, к смежному с ним и т.д.
Считается, что эти уточнения исключают возможность рассматривать в качестве одного многогранника многогранники, состоящие из суммы двух и более многогранников и соприкасающиеся между собой лишь вершинами или ребрами. Например, так, как показано на Рис. 2.
Рис. 2 Пример соприкасающихся вершинами пирамид
Казалось бы, зачем вводить специальные уточнения? Ведь для того, чтобы определиться одна перед нами фигура, или нет и какая всего лишь надо четко описать место контакта вершин пирамид. Если говорить точнее, то достаточно описать площадку их контакта. И вариантов такого описания очень мало - всего два.
По первому варианту площадь контакта равна нулю, и тогда внутренние объемы пирамид разобщены и совершенно очевидно, что мы имеем дело с двумя очень близко расположенными друг к другу, но не объединенными в одной фигуре пирамидами.
По второму варианту площадь контакта отлична от нуля, и тогда через площадь контакта внутренние объемы пирамид окажутся, объединены и совершенно очевидным будет, что в этом случае мы имеем дело с одной фигурой, сложенной из двух пирамид.
Казалось бы, все очень просто, но все дело в том, что имеется в виду контакт вершин пирамид в одной единственной точке. Т. е. для того, чтобы определиться с тем, что же изображено на Рис. 2 необходимо, немного немало, определиться с параметрами (в данном случае размерами) геометрической точки. Но как же это сделать, если при том, что точка, являясь одним из основных понятий геометрии, так до наших дней и не имеет четкого определения. Причем безуспешно пытаются дать ее определение уже не десятки и даже не сотни, а тысячи лет. Ведь если бы это удалось, то, например, можно было бы отличать точку от очень короткого отрезка и как следствие число Пи, связывающее длину окружности и диаметр окружности, стало бы конечным. Больше по поводу важности этой проблемы можно уже ничего не говорить.
Т. е. проблема определения геометрической точки очень старая и возможно даже в принципе исчерпывающе неразрешимая. Для того чтобы уйти от столь неудобной проблемы и были введены уточнения в определение многогранников запрещающие существование многогранников в виде фигур изображенных на Рис. 2.
Пока многогранники можно было описать лишь словесными формулировками или при помощи рисунков выбранный подход к определению многогранников к противоречиям не приводил. Однако все изменилось с появлением уравнений задающих многогранники (см. статью "Уравнение многогранников" http://stob2.narod.ru/29s.htm). Иначе говоря, функциональных зависимостей графиком, которых являются многогранники.
Как известно, каждой функции соответствует свой график и никакими изменениями коэффициентов или суммированием функций принципиально изменить график, задаваемый функцией невозможно. Любой сомневающийся, в этом легко может убедиться, взяв для эксперимента сравнительно простую линейную функцию: y=a*x+b. Как бы ни изменялись значения коэффициентов a и b, как бы не складывались эти функции, все равно графиком получающихся функций всегда будет прямая линия.
Таким образом, получается, что любая геометрическая фигура, построенная при помощи системы уравнений (1) или суммы этих уравнений будет являться многогранником и только многогранником, так как при помощи системы уравнений (1) ничего иного построить невозможно. При этом очень наглядно вскрываются противоречия, заложенные в определения многогранников при помощи неестественных уточнений.
Так, например, в анимации на Рис. 1 периодически появляется геометрическая фигура, которую принято идентифицировать, как шар, но она, как и все остальные фигуры в анимации была построена при помощи системы уравнений (1) и, следовательно, может быть только многогранником.
Впрочем, это противоречие очень легко устраняется, если под шаром понимать некий идеализированный потенциально существующий многогранник, который может быть тоже лишь потенциально построен при помощи системы уравнений (1) при L1 = L2 больших нуля и при N1 = N2 стремящимся к бесконечности.
Сложение систем уравнений (1) с различными значениями коэффициентов позволяет формировать различные многогранники. От фигуры, приведенной на Рис. 2, которою под чисто надуманными предлогами предлагается не считать многогранником. До многогранника показанного на Рис. 3. Многогранники подобные, изображенному на Рис. 3, официальной наукой относятся к многогранникам и называются звездчатыми самопересекающимися.
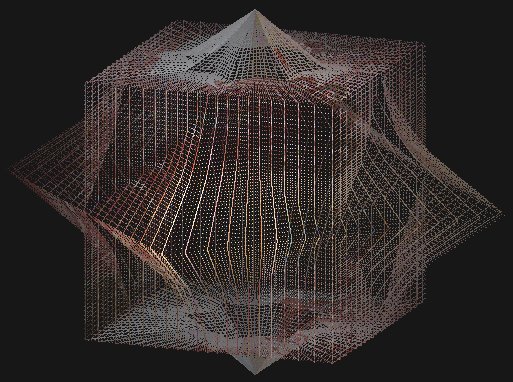
Рис. 3 Пример звездчатого самопересекающегося многогранника построенного, как график от суммы двух систем уравнений (1) с различными коэффициентами
Кстати звездчатые самопересекающиеся многогранники могут быть получены и без суммирования систем уравнений (1). Для этого при построении многогранника при помощи системы уравнений (1) достаточно выбрать для коэффициента N1 и(или) N2 нецелочисленные значения, а углы сферических координат брать из интервала превышающего 2π .
На Рис. 4 показана анимация построения звездчатого самопересекающегося многогранника при помощи системы уравнений (1) при N1 =2,5, а N2 =4.
Рис. 4 Анимация построения примера звездчатого самопересекающегося многогранника при помощи системы уравнений (1)
Подобных звездчатых самопересекающихся многогранников может быть бесконечно много. Это было показано в ходе исследований построения звездчатых самопересекающихся многоугольников в статье: "Уравнение правильных многоугольников в полярных координатах" http://stob2.narod.ru/27s.htm. Так, что приведенный на Рис. 4 многогранник никак не может рассматриваться в качестве какого-то единичного исключения.
Очевидно, что многогранники на Рис. 3 и 4 значительно отличаются друг от друга и в качестве самопересекающихся могут рассматриваться только многогранники подобные многограннику изображенному на Рис. 4.
Анимация на Рис.4 очень хорошо показывает главное отличие демонстрируемого многогранника от всех прочих многогранников. Это отличие состоит в наличие внутренних полностью замкнутых полостей. И именно наличие этих полностью замкнутых полостей делает этот многогранник несоответствующим общепринятым в настоящее время определениям многогранника, что приводит к еще одному противоречию между результатами от применения этих определений и системы уравнений (1).
Однако такие неправильные с точки зрения официальной науки многогранники слишком важны и очень широко распространены. Дело в том, что внутренние полости могут иметь не только самопересекающиеся многогранники, а, например, такие, как показанный при помощи анимации на Рис. 5.
Рис. 5 Анимация построения выпукло-вогнутого многогранника с полностью замкнутой внутренней полостью
Интересно, что если в многограннике, показанном на Рис. 5, проделать дыру, ну, например, так, как показано на Рис. 6, то он вдруг сразу начинает соответствовать официальному определению многогранника. Кстати топологи тоже вздохнут с облегчением и заявят, что эта фигура гемеоморфна сфере. Если в этой фигуре проделать больше дыр - тоже не беда, т. к. она станет гемеоморфна бублику с некоторым количеством дыр. А вот, то, что показано на Рис. 5 ничему не соответствует, а значит лучше сказать, что, и не существует вовсе. И это весьма забавное обстоятельство способно породить лишь очень нехорошие мысли по поводу достоверности официального определения многогранника.
Рис. 6 Пример выпукло-вогнутого многогранника с дырой связывающей между собой его внешнюю и внутреннюю поверхности
Почему эти многогранники важны? Да потому, что они представляют собой такие очень широко распространенные, как в природе, так и в технике объекты, как оболочки. И, если говорить иначе, то получается, что все оболочки по своей геометрической форме представляют собой многогранники. Причем это относится, как к оболочкам с отверстиями, так и к оболочкам без отверстий.
В статье "Земля - гигантский поликристалл" http://stob2.narod.ru/8i.htm было показано, что наиболее точно форму Земли передает многогранник. Но это справедливо для внешней ее поверхности, если же мы хотим полностью описать твердую поверхность Земли, то из-за наличия у нее жидкого ядра ее придется представлять в виде оболочки по своей форме схожей с многогранником, показанным на Рис. 5.
С большой долей вероятности можно ожидать, что и форма нашей Вселенной тоже будет в определенной мере подобна многограннику, показанному на Рис. 5. Ведь после Большого взрыва вряд ли много материи могло остаться непосредственно вблизи точки взрыва. В центре взрыва обычно образуется зона разряжения. Т. е. можно ожидать, что материя расширялась, как оболочка, которая впоследствии под действием гравитационных, центробежных и иных сил претерпела деформации и образование в своей структуре многочисленных разрывов (дыр). И упрощенно наша Вселенная по своей форме должна бы напоминать многогранник, показанный на Рис. 7. Да и человеческое тело, начиная прямо с кожного покрова, по сути, состоит из суммы многогранных оболочек.
Рис. 7 Упрощенная форма Вселенной в виде многогранника с внутренней полостью
В общем, оболочек в виде многогранников вокруг нас очень много и мы все даже живем внутри них. Именно поэтому следовало бы заняться в первую очередь изучением не особо красивых правильных многогранников (тел Платона), а их менее привлекательных выпукло-вогнутых многогранников с внутренними полостями, которым, как это не странно официальная наука отказывает даже в праве на существование. И это происходит на фоне того, что так называемые правильные многогранники были выделены в отдельный вид при помощи чисто надуманных и ничем объективно не обоснованных правил.
Исследование системы уравнений (1) показывает, что кроме уже описанных видов многогранников существуют и другие, тоже достаточно важные их разновидности. На рис. 8 представлены примеры торообразных многогранников или так называемых многогранников с дырой, о возможности, существования которых нечасто, но все же ранее упоминалось в литературе.
Рис. 8 Примеры торообразных многогранников или примеры многогранников с дырой
Теперь, если частично или полностью увеличить до очень большого количества число граней (обычно достаточно увеличить до нескольких тысяч) в торообразных многогранниках, то можно получить примеры (см. Рис. 9) торообразных многогранников, которые выглядят, как геометрические фигуры с криволинейными поверхностями.
Рис. 9 Примеры торообразных многогранников, которые выглядят, как геометрические фигуры с криволинейными поверхностями
Действительно, любой, кто посмотрит на Рис. 9 будет уверен в том, что он видит там тор и кольца с идеальными цилиндрическими поверхностями, но это совсем не так. Просто монитор нашего компьютера и наши глаза не имеют достаточного разрешения, для того, чтобы увидеть, что все поверхности фигур на Рис. 9 образованы громадным количеством граней (плоских многоугольников). Причем уравнения при помощи, которых были сгенерированы эти изображения, действительно строили их, как многогранники.
Поэтому, вообще то, тор, цилиндрические кольца и т. п. фигуры следует рассматривать, как некие идеализированные потенциально существующие многогранники с бесконечно большим количеством граней.
Кроме уже описанных здесь необычных многогранников с помощью системы уравнений (1) удалось выявить тоже сравнительно важные и, наверное, самые необычные многогранники, о существовании которых ранее вообще не упоминалось. Это спиральные многогранники (Рис. 10) и винтовые многогранники (Рис. 11).
Рис. 10 Пример спирального многогранника в виде плоской спирали
Рис. 11 Пример винтового многогранника в виде винтовой линии
Если в спиральных или винтовых многогранниках увеличивать количество граней, то с определенного момента они тоже будут неотличимы от геометрических фигур с криволинейными поверхностями. Например, на Рис. 12 показан пример многогранника визуально неотличимого от геометрической фигуры с криволинейной поверхностью. Но от этого многогранник, конечно, не может перестать быть многогранником.
Рис. 12 Пример винтового многогранника визуально неотличимого от геометрической фигуры с криволинейной поверхностью
Эти многогранники являются выпукло-вогнутыми и наглядно демонстрируют возможность существования бесконечных многогранников, так как витки спиралей в спиральных и винтовых многогранниках можно достраивать бесконечно. Во всяком случае, объективных препятствий для этого не существует кроме чисто надуманного ограничения введенного в определение многогранника, по которому число граней у многогранника должно быть обязательно конечным.
Необходимо отметить, что при построении торообразных, спиральных и винтовых многогранников в систему уравнений (1) потребовалось ввести изменения. О характере изменений можно посмотреть в статье: "Уравнение спиралей в виде многоугольников в полярных координатах" http://stob2.narod.ru/28s.htm. Получается, что эти многогранники задаются вроде бы, как другими функциональными зависимостями, отличными от системы уравнений (1) и, недолжны бы, относиться к многогранникам. Но в данном случае тело многогранника строится все же за счет использования системы уравнений (1), а внесенные в эту систему уравнений изменения влияют лишь на общую форму многогранника. Поэтому серьезного противоречия здесь не возникает.
Из приведенных в статье примеров видно, что многогранники могут иметь форму всех основных базовых геометрических объектов. Таких, как шар, тор, оболочка, спиралевидные образования. Таким образом, все реально существующие в нашем мире объекты имеют геометрическую форму многогранника или суммы многогранников и в принципе иной геометрической формы иметь не могут.
Кроме этого и все идеализированные существующие лишь потенциально объекты по своей геометрической форме являются тоже многогранниками, идеализированными многогранниками. Это, прежде всего, такие объекты, как точка, отрезок, прямая, вообще любая линия, многоугольник, как часть плоскости, окружность, круг, шар, тор и многие другие.
Все эти объекты можно представить лишь, как идеализированные многогранники в связи с тем, что при их построении в системе уравнений (1) предполагается полностью или частично придавать бесконечно большие или бесконечно малые значения следующим коэффициентам: L1, L2, N1, N2.
Для примера на Рис. 13 показан шестиугольный многоугольник являющийся частью плоскости и построенный при L2 стремящемся к нулю, N1=6, N2=4
Рис. 13 Шестиугольный многоугольник являющийся частью плоскости и построенный при помощи уравнений многогранников
А на Рис. 14 показана анимация перехода призмы в отрезок при L2 стремящемся к нулю, N1 стремящемся к бесконечности, N2=4.
Рис. 14 Анимация перехода призмы в отрезок построенная при помощи уравнений многогранников
Аналогично при помощи системы уравнений (1) можно приближенно построить и иные идеализированные потенциально существующие объекты.
Почему идеализированные объекты можно построить лишь приближенно? Потому, что невозможно указать точный минимальный размер точки или длины (толщины) отрезка. Каждый раз, выбрав какой то конкретный размер можно всегда указать еще более маленькую величину и так до бесконечности. Именно поэтому каждое нарисованное изображение точки, линии и так далее является компромиссным и зависит в основном от возможностей человеческого зрения. Так как ясно, что если, например, на Рис. 14 и дальше продолжить уменьшать толщину отрезка, то очень быстро настанет момент, после которого человек просто перестанет его видеть, а монитор чисто по техническим причинам не сможет его отображать.
В описании идеализированных потенциально существующих объектов есть еще один интересный вопрос. Этот вопрос связан с тем обстоятельством, что существует множество широко известных функциональных зависимостей задающих окружность, прямую линию, эллипс и т. п. объекты. Описывать один и тот же объект двумя различными функциональными зависимостями вроде бы нельзя. Получается, вроде бы имеем противоречие.
Однако никакого противоречия тут нет. Просто все привыкли к тому, что считается, что эти известные уравнения описывают именно эти объекты. На самом же деле они описывают лишь множества значений координат, через которые проходят эти идеализированные объекты, но никак не сами эти объекты. Для практических нужд такого описания пока обычно бывает достаточно. Но при этом никто не спешит ставить знак равенства между понятием геометрической точки и понятием координат ее местонахождения в пространстве. А это фактически означает, что описать идеализированные потенциально существующие объекты можно только исключительно при помощи системы уравнений (1) и ее модификаций.
март 2011 года
|