Старый новый взгляд на природу Информации (HJ)
Intro
Размышления о природе Информации продолжаются с тех пор, как это слово перешло из языка теологов в жаргон инженеров. Может показаться неожиданным, но за почти семьдесят лет развития (считая от пионерных работ Клода Шеннона) и хорошо разработанный математический аппарат, до сих пор не существует общепринятого представления о том, что есть Информация. Это порождает многочисленные споры. Трудно указать другую дисциплину, предмет которой был бы столь же неясен. В настоящее время, природа Информации предмет бесчисленных философских спекуляций. Не существует ни общепринятой, ни даже правдоподобной точки зрения на природу Информации.
Два основных конфликтующих направления расходятся, считать ли Информацию свойством, изначально присущим материальному физическому агенту (чему пока доказательств не найдено), либо полагать ее идеальной величиной, формальным параметром, переменной в уравнении. В технических дисциплинах неявно придерживаются второй точки зрения, свободно оперируя "количеством информации", также, как это, например, делается с "мнимыми" числами.
Классический подход к коммуникации
В повседневной жизни, мы большей частью стараемся иметь дело с локально линейными объектами Пространства-Времени, где прямая - кратчайшее расстояние: "срезаем углы" и перебегаем дорогу на красный свет. К сожалению, в целом Вселенная устроена весьма нелинейно - в гости к соседу из соседнего подъезда приходится ходить через улицу, а не через пролом в стене.
Идеализированные линейные (евклидовы) миры изучены и интуитивно понятны лучше всего. Встречая нелинейность, мы прежде всего задумываемся, нельзя ли ее как-либо "линеаризовать". Один из способов "линеаризации" - поиск таких характеристик, которые позволяли бы "линейно" сопоставлять нелинейные объекты сложной конфигурации. Исторически первыми, очевидно, были меры расстояния, веса, объема и времени. В сущности, все они были взаимозаменяемы. Расстояние могло определяться в днях пути, время - объемом вытекшей из клепсидры воды, объем - весом сосуда. Даже в наше время, несложно представить работу "от забора - до обеда". Развитие технологий очень быстро добавило к списку измерение площадей и универсальную меру для всего - деньги. Деньги, как единая мера всех вещей, обладали тремя важными качествами:
- Измеримость. Их удобно считать.
- Аддитивность. Их можно накапливать.
- Упорядоченность. Можно указать, у кого их больше.
Идея универсальной валюты сыграла важную роль в экономике, но главный ее триумф - все есть Энергия - случился в физике, завершившись самой знаменитой в истории формулой Теории Относительности Эйнштейна
E = m * c^2
Первые попытки математически описать передачу текстов были предприняты Ральфом Хартли.
"На основе физических (а не физиологических) соображений установлена количественная мера "информации" ... Показано, что когда накопление энергии накладывает ограничение при стационарной передаче на предельную полосу частот, то количество информации, которое может быть передано, пропорционально произведению полосы частот на полезное время".
В 1927 году на международном конгрессе по телефонии Хартли выдвинул первый формальный вариант такой оценки (мера Хартли)
"Для того чтобы мера информации имела практическую, инженерную ценность, она должна быть такой, чтобы информация была пропорциональна числу выборов. Поэтому число возможных последовательностей не годится для непосредственного использования в качестве меры информации. Однако его можно использовать как основу для построения производной меры, удовлетворяющей практическим требованиям. Для этого будем произвольно считать, что количество информации пропорционально числу выборов, а коэффициент пропорциональности выберем таким образом, чтобы равным числам возможных последовательностей соответствовали равные количества информации"
H = n * Log(s)
Интересно, что при обосновании своего предложения, Хартли апеллирует к аналогии с мощностью:
"Сделанное нами сводится, следовательно, к тому, что в качестве практической меры информации мы берем логарифм числа возможных последовательностей символов. Положение сходно с тем, которое мы встречаем при измерении затухания, вносимого включением некоторого звена в систему телефонной передачи. Эффект от такого включения сводится к изменению в некотором определенном соотношении мощности, отдаваемой приемнику. Это соотношение можно принять в качестве затухания. Однако оказывается более удобным взять в качестве меры затухания логарифм отношения мощностей".
Более того, будучи радиоинженером, он вводит энергетический инвариант:
"Это приводит нас к важному выводу, что максимальная скорость передачи информации, возможная в системе, частотный диапазон которой ограничен некоторой областью, пропорциональна ширине этой полосы частот. Отсюда и следует, что общее количество информации, которое может быть передано посредством такой системы, пропорционально произведению передаваемой полосы частот на время, в течение которого система используется для передачи. Произведение передаваемой полосы частот на время и есть упомянутый мною в начале статьи количественный критерий сравнения передающих систем"
В главе "Измерение информации" Хартли пишет:
"...рассмотрим, с какими факторами мы имеем дело в связи, осуществляется ли она по проводу, путем устной речи, письма или каким-либо другим способом. Прежде всего должна существовать группа физических символов - слов, точек, тире и т.п., имеющих по общему соглашению известный смысл для корреспондирующих сторон. В любой данной передаче отправитель мысленно выбирает тот или иной символ и путем какого-либо материального процесса (bodily motion), например своим голосовым аппаратом, направляет на этот символ внимание получателя. В результате последовательных выборов вниманию получателя предлагается последовательность символов. При каждом выборе исключаются все другие символы, которые тоже могли быть выбраны".
Иными словами, для рассматриваемой Хартли коммуникации требуются:
- Две корреспондирующие стороны.
- Группа физических символов имеющих известный смысл.
- Фиксированный набор вариантов (исключаются все другие символы, которые тоже могли быть выбраны).
Указанный набор требований будем называть Разделяемой моделью.
Например, при игре в "морской бой" или в шахматы, играющие разделяют правила игры, набор фигур, игровое поле.
Хартли отказывается от рассмотрения того, что есть Информация, сосредоточиваясь исключительно на технических аспектах передачи сообщений. Он пишет: "То, что я надеюсь достичь в этом направлении, должно установить количественную меру, посредством которой могут быть сравнены мощности различных систем передачи информации"
Две важных идеи Хартли, позднее детально разработанные Шенноном, это введение "энергетического инварианта" ("общая сумма информации, которая может быть передана, пропорциональна переданному частотному диапазону и времени передачи") и "согласование сообщений и линий".
В поисках подходящей оценки для сообщений, Шеннон, несомненно, придерживался той же концепции "денежного эквивалента", позволявшего бы сравнивать разнородные тексты "по стоимости".
Во время второй мировой войны Шеннону пришлось участвовать в работе групп управления зенитным огнем и в разработке криптографических систем, в том числе правительственной связи. Тогда же он встретился с Норбертом Винером.
Винер писал в своих воспоминаниях:
"Я подошел к теории информации с позиций изучения электрических систем, проводящих непрерывный ток или что-нибудь такое, что по крайней мере можно интерпретировать как непрерывный ток. В то же время Клод Шеннон из лаборатории телефонной компании Белла параллельно разрабатывал близкую и во многом эквивалентную теорию с точки зрения теории электрических переключательных схем. Эта работа представляла собой непосредственное развитие его предыдущих работ, посвященных использованию алгебры логики для решения задач теории релейных схем ... Шеннон любит дискретное и сторонится непрерывного. Он рассматривает дискретные сообщения как последовательность во времени утвердительных и отрицательных ответов, и каждый выбор между «да» или «нет» считает элементом информации. В то же время я, занимаясь теорией непрерывной фильтрации и исходя из точек зрения, казавшихся вначале совершенно отличными от точки зрения Шеннона, пришел к весьма близкому определению единицы количества информации. Введя определение понятия количества информации по Шеннону-Винеру (ибо оно в равной мере принадлежит нам обоим), мы совершили радикальный переворот в этой области".
Приступив к решению задачи Транспорта сообщений, Шеннон неявно пришел к двухкомпонентной модели сообщения - несжимаемая (жидкая) фаза (энтропия) и сжимаемая (газовая) фаза (избыточность). Очевидно, при транспортировке можно устранить бесполезную сжимаемую фазу и оставить только несжимаемую часть. Это называется "сжатием" сообщений (эффективное кодирование). Термин "сжатие", полностью неверен, но широко устоялся и будет использован по историческим причинам.
В классической теории, сигналу приписывается некоторая числовая величина ("количество информации"), тем большая, чем выше расхождение между моделями. Если состояния моделей оказываются идентичны, говорят, что сигнал не несет никакой (новой) информации. По Шеннону, сигнал имеет смысл ошибки прогноза.
Шенноном была улучшена оценка Хартли, применимая только к сообщениям с равной кратностью всех символов. Шеннон обобщил ее на случай сообщений с неравной кратностью. В статье "Математическая теория связи" (1948) Клод Шеннон в точности повторяет основные тезисы Хартли и, вслед за ним, также отказывается обсуждать семантические аспекты передачи сообщений и природу Информации. Вот как Шеннон описывает цели коммуникации:
"Основная задача связи состоит в точном или приближенном воспроизведении в некотором месте сообщения, выбранного для передачи в другом месте. Часто сообщения имеют значение, т. е. относятся к некоторой системе, имеющей определенную физическую или умозрительную сущность, или находятся в соответствии с некоторой системой. Эти семантические аспекты связи не имеют отношения к технической стороне вопроса. Существенно лишь, что посылаемое сообщение является сообщением, выбранным из некоторого множества возможных сообщений".
В этой же статье Шеннон приводит пятизвенную диаграмму - "Общую схему системы связи", состоящую их Источника информации, Кодирующего устройства, Канала связи, Декодирующего устройства и Приемника.
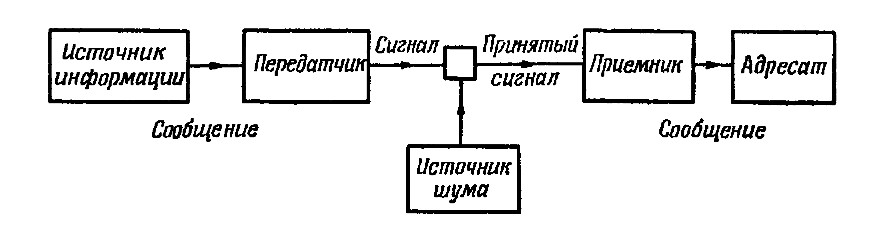
Описанное К. Шенноном устройство (такое, как электрический телеграф, например) представляет из себя Повторитель сигнала или Копир, воспроизводящий на выходе входной сигнал за счет работы третьих сил. Под такое определение попадает множество устройств, например, рычажные весы, две чаши которых служат Источником и Приемником сигнала, а коромысло - Каналом связи между ними. Иными словами, диаграмма Шеннона эквивалента схеме уравновешивающего Измерителя, а Информационный процесс можно рассматривать как процесс Измерения.
В этой же статье Шеннон обобщает характеристику "количества информации", введенную Хартли и вводит понятие (информационной) Энтропии и Избыточности, имеющих важное значение в техниках сжатия данных (По хартли - "согласование сообщений и линий").
Шеннон пишет об этом так:
"Отношение энтропии источника к максимальному значению, которого могла бы достичь энтропия при тех же символах, назовем относительной энтропией источника. Как будет показано ниже, она является максимальным сжатием, которое можно осуществить кодированием при помощи того же самого алфавита. Единица минус относительная энтропия есть избыточность
...
Для передачи максимальной мощности от генератора в нагрузку в общем случае применяется трансформатор, делающий сопротивление генератора, наблюдаемое со стороны нагрузки, равным сопротивлению этой нагрузки. Это аналогично рассмотренной выше ситуации: преобразователь, осуществляющий кодирование, согласовывает источник с каналом в статистическом смысле. Источник, рассматриваемый через преобразователь со стороны канала, должен иметь такую же статистическую структуру, какую имеет источник, который максимизирует энтропию в канале".
Шеннон вводит понятие энтропии аксиоматически, постулируя некоторые свойства и доказывая, что такая функция существует и единственна. В своих рассуждениях он использует дерево выбора и принцип неразрывности потока - полный поток по дереву равен сумме потоков всех ветвей. Шеннон использует поток вероятности, но это неважно: те же самые рассуждения применимы к произвольной распределительной системе.
Для того чтобы быть мерой (аналогом мощности) искомая функция должна обладать важным свойством: мера (мощность) полного дерева должна быть равна сумме мер (мощностей) всех его частей.
Шеннон рассуждает так:
"Предположим, что имеется некоторое множество возможных событий, вероятности осуществления которых суть p1, p2 ... рn. Эти вероятности известны, но это - все, что нам известно относительно того, какое событие произойдет. Можно ли найти меру, того, насколько велик "выбор" из такого набора событий или сколь неопределенен для нас его исход?
1. H должна быть непрерывной относительно р[i].
2. Если все р[i] равны, р[i] = 1/N, то Н должна быть монотонно возрастающей
функцией от N. В случае равновероятных событий имеется больше возможностей
выбора или неопределенности, чем в случае, когда имеются разновероятные
события.
3. Если бы выбор распадался на два последовательных выбора, то первоначальная
H должна была бы быть взвешенной суммой индивидуальных значений H. Смысл этого
иллюстрируется следующим рисунком:
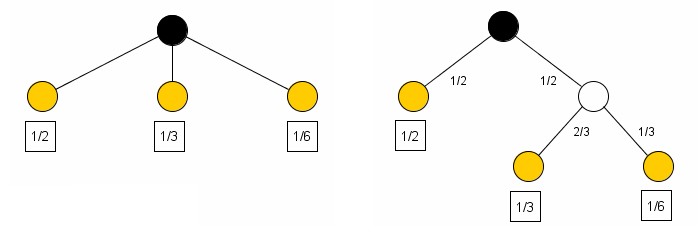
Слева имеются три возможности p1 = 1/2; р2 = 1/3; р3 = 1/6. Справа производится выбор между двумя возможностями, причем каждая имеет вероятность 1/2, и в случае осуществления второй возможности производится еще один выбор между двумя возможностями с вероятностями 2/3; 1/3. Окончательные результаты имеют те же самые вероятности, как и прежде. Потребуем в этом конкретном случае, чтобы
H(1/2, 1/3, 1/6) = H (1/2, 1/2) + 1/2 * H (2/3, 1/3)
Коэффициент 1/2 является весовым множителем, введенным из-за того, что второй выбор осуществляется только в половине всех случаев".
Два первых пункта ничего не прибавляют к тому, что предлагал Хартли. Третий пункт, как ни странно, также не привлекает внимания комментаторов. Между тем, деревья слева и справа имеют различное строение и нет никакой формальной процедуры, позволяющей их уравнивать.
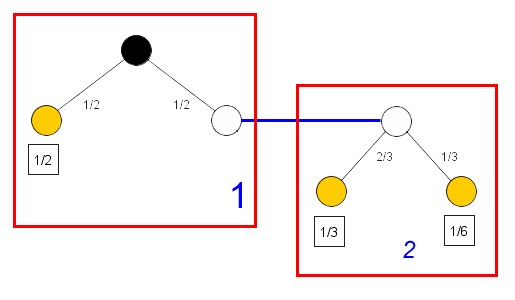
Шеннон разбивает полную систему на две и требует равенства меры полной системы взвешенной сумме мер подсистем. Введение весового множителя особенно интересно, так как не имеет прямого аналога в невероятностных цепях. Фактически, Шеннон расматривает это дерево как переключательную схему, половину времени находящуюся в "левом" положении и половину - в "правом".
Таким образом, Шеннон эквивалентирует различные деревья (с различной размерностью). В сущности, эта возможность уравнивания различных по структуре деревьев выбора (суть, различных сообщений) и есть важнейшее свойство энтропии, как меры на дереве выбора.
Из использованного Шенноном трюка с расщеплением ветви следует, что коэффициенты передачи ветвей перемножаются при их "сложении". Вывод формулы энтропии полностью основан на постулировании этого свойства:
k(1/2) + k(2/3) = k(1/3)
и
k(1/2) + k(1/3) = k(1/6)
Логарифм является единственной функцией, отвечающей этому условию, и задав формулу "сложения" ветвей дерева, Шеннон задает и логарифмическую меру на дереве.
Парадоксально, но "любивший дискретное и сторонившийся непрерывного" Клод Шеннон, избрал математическим аппаратом новой дисциплины теорию случайных процессов. Судя по списку благодарностей, его увлекла интерпретация Норберта Винера. Случись так, что Шеннон остался бы в рамках дискретной модели, энтропия была бы описана в терминах комбинаторики, а рядом с "энергетическим инвариантом" Хартли стоял бы "энтропийный инвариант" Шеннона.
Критика классического подхода
Несмотря на успехи классического подхода, в нескольких аспектах он выглядит неудовлетворительным:
- Не сформулировано само понятие "Информация"
- "Неопределенность" или "Количество информации" приписано сообщению
- Скрыто неявное использование Источником и Приемником общей (разделяемой) модели
- Понятию "Энтропия" не придано никакого физического содержания
Понятие "Информация" требует предварительного определения Модели.
Сама возможность выбора, о которой пишут Хартли и Шеннон, указывает на заранее заданный набор вариантов.
Как уже было сказано ранее, для коммуникации необходимы две стороны и техническая возможность связи между ними. Стороны должны разделять общий алфавит, общий язык, общий словарь, общий набор правил итп. Полный набор сущностей, разделяемых обоими сторонами, и не изменяющийся за время коммуникации, будем называть Разделяемой моделью.
При игре в шахматы, например, разделяются сама шахматная доска, набор фигур и правила игры.
Модель может находиться в различных состояниях, по сигналу переходя из одного состояния в другое. Одному и тому же сигналу могут соответствовать различные модели с различной "неопределенностью". Это означает, что "количество информации" не может быть приписано сообщению, а только модели.
С точки зрения коммуникации, неважен ни вид сообщения, ни его битовый размер, ни информационная энтропия, ни колмогоровская сложность. Важно только, что сигнал переводит систему из одного состояния в другое.
Пример:
Некий полиглот, владеющий ивритом, английским и русским, в ходе сеанса, где с равной вероятностью может быть передан любой символ алфавита, получает символ A. В алфавите иврита 22 буквы, в латинском 26, в русском - 33. "Устраненная неопределенность" никак не зависит от использованного символа и полностью относится к выбранной модели (использованному алфавиту).
Само по себе сообщение лишено смысла и обретает его только в рамках разделяемой модели и текущего контекста. Табуированные слова могут быть замены эвфемизмами. Перевод на другой язык сохраняет смысл текста, но безнадежно деформирует сообщение. Фраза "кушать подано" имеет тот же самый смысл независимо от того, кем из лакеев она сказана. Смысл идиом часто вовсе не связан с буквальным содержанием фразы (например, "собаку съел"). В жаргонах (таких, как "феня") многие понятия часто заменяются словами других языков, а термины искажаются без потери смысла.
Предложенный Шенноном неудачный термин "количество информации" породил заблуждение, будто сообщения являются переносчиком информации.
Сигнал не имеет смысла вне контекста модели. Это только указание на переход из одного состояния в другое. Лишь в заданном контексте сообщение может приобрести смысл (или не иметь его вовсе).
В литературе не раз обыгрывался сюжет, когда два человека, наблюдающие то же самое явление (тот же самый сигнал), используют различающиеся модели и приходят к различным выводам. Как пример, дуальные пары Шерлок Холмс и доктор Ватсон или Белый Человек и Чингачгук - Большой Змей.
Эту разницу моделей хорошо иллюстрирует следующий анекдот: Как отличить электрика от учителя геометрии Попросить назвать антоним к слову "параллельно". Электрик скажет "последовательно", а учитель геометрии - "перпендикулярно".
Под "Информацией" будем понимать нахождение модели в данном конкретном состоянии..
Например, нормальная температура тела 36.5 градусов по температурной шкале Цельсия.
Иными словами, Информация - это состояние, выбранное в результате реакции на сообщение.
В этом определении важно, что Информация - это результат процесса выбора.
Физический процесс заключается просто в переносе вещества/энергии. Но под Информационным процессом всегда будем понимать только процесс выбора одного варианта из набора вариантов под действием входного сигнала.
Понятие энтропии рассмотрим на примере игры с угадыванием чисел. Пусть загадано число от единицы до восьми и разрешено отвечать на вопросы только Да и Нет. Как должна выглядеть оптимальная стратегия игры? Сколько вопросов нужно задать для гарантированного получения ответа?
Все пространство состояний содержит восемь вариантов ответа. Разделим это пространство пополам - четыре + четыре. Правильным вопросом, на который можно ответить Да/Нет будет вопрос, содержит ли загаданное число выбранная половине пространства состояний (Это число больше четырех?). Теперь делим пополам найденную половину. Не больше чем за три вопроса можно выяснить загаданное число. Это соответствует следующему дереву выбора:
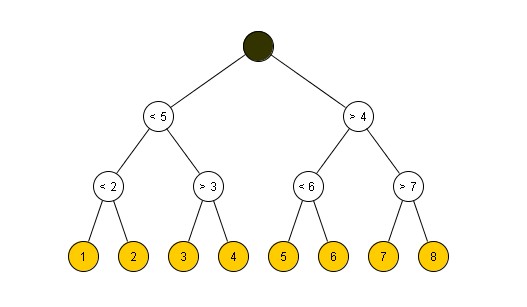
Высота этого бинарного дерева (мера Хартли) равна двоичному логарифму числа состояний: H = Log2(8) = 3.
Путь от корня дереву до любого листа (заданного числа) требует не более трех шагов.
Заметим, что все варианты выбора равновозможны. Условимся называть такое дерево выбора деревом Хартли.
Для равновероятных выборов оценка Хартли является кратчайшим путем по дереву выбора. Экстремальные свойства энтропии удобны во многих приложениях, но ее применение имеет смысл только в упорядоченных пространствах, о чем нередко забывают.
Рассмотрим тот же пример выбора, только на этот раз пусть восемь биллиардных шаров перенумерованных от одного до восьми лежат в желобе по порядку номеров. Действуя по тем же правилам, не более чем за три шага можно определить загаданный шар.
Изменим теперь игру так, что шары будут расположены в произвольном порядке. Тогда понятие энтропии теряет всякий смысл для выбора: номер шара уже ничего не говорит о его положении в желобе.
Точно также и энтропия Шеннона имеет смысл только для текстов или иных последовательностей, в которых задан алфавитный порядок.
Новый взгляд на коммуникацию
Будем различать физический и информационный процессы.
Физический процесс реален. Это процесс переноса. Он всегда связан с перемещением вещества/энергии.
Информационный процесс виртуален. Ничего не перемещается. Информация всегда только копируется.
Коммуникация является одновременно и физическим и информационным процессом и важно тщательно разделить эти компоненты.
При описании коммуникации не рассматриваются физические характеристики системы (материал носителя, потребление энергии, время передачи итп). Если "энергетикой" процесса можно пренебречь - не потому, что обмен незначителен, а поскольку, его учет ничего не прибавляет к сути коммуникации, то такую модель коммуникации, в которой заведомо отказываются от учета обмена массой/энергией, а изменения поведения приписываются "передаче информации", будем называть Информационным процессом. Информационный процесс - это всегда "безэнергетический" процесс, упрощенная модель реального физического процесса.
Вопреки устоявшемуся словосочетанию "обмен информацией", Информация не переносится и не "обменивается". Информация неперемещаема и может быть только скопирована. Чтение книги не уничтожает уже прочитанный текст. Ксерокопия не влияет на оригинал. Если физические предметы (например, деньги) являются предметом обмена и в каждый данный момент имеют только одного владельца, информация может быть разделена между произвольным количеством лиц так, что каждый будет иметь свою собственную точную копию.
По меткому замечанию, приписываемому Бернарду Шоу ("Парадокс Шоу"):
"Если у вас есть яблоко и у меня есть яблоко, и мы обменяемся этими яблоками, то у каждого из нас будет по яблоку. Но если у вас есть идея и у меня есть идея, и мы обменяемся этими идеями, то у каждого из нас будет по две идеи."
Справедливости ради, словари утверждают, что Б. Шоу никогда не произносил этих слов и, на самом деле, изречение принадлежит Charles Franklin Brannan. Но, согласно принципу Арнольда: "Если какое-либо понятие имеет персональное имя, то это - не имя первооткрывателя".
Основываясь на "Парадоксе Шоу", как на необходимом и достаточном условии, можно испытать и отвергнуть любую предъявляемую сущность, претендующую быть Информацией, если она не обладает свойством неперемещаемости и/или не может быть скопирована.
Физика и Кибернетика по-разному смотрят на мир.
Физика изучает Силы, приложенные к объекту. Под действием Сил он деформируется. Эта деформация рассматривается как реакция на воздействие, уравновешивающая его. В момент равновесия, сумма всех сил в узлах и по контурам равна нулю - два закона Кирхгофа. Таким образом, Физика основана на знании "анатомии" объекта, его "скелета".
Кибернетика вовсе не интересуется внутренним устройством объекта и игнорирует Силы. Кибернетика приписывает реакцию объекта действию фиктивного агента - Сигналу. В кибернетической модели объект получает входной сигнал и реагирует выходным сигналом, без всякого учета энергетики процесса. Там, где Физика изучает равновесие Сил, Кибернетика - обмен сигналами. Обмен Сигналами - это и есть Коммуникация.
Коммуникация - способ построения фиктивной модели взаимодействия (с акцентом на существенные аспекты) поверх реального физического процесса.
Если процесс может быть описан несколькими различными моделями (неважно, корректными или нет), обе стороны должны разделять ту же самую функционально идентичную модель.
Преимущество "кибернетической" модели - в выделении значимых связей при игнорировании деталей реализации, недостаток - полная "нефизичность". Кибернетика лишена возможности установить осуществимость модели и реальные силы, приводящие ее в движение.
Как правило, инженеры имеют дело с сильными взаимодействиями: машины и механизмы, высоконагруженные конструкции, мощные энергосети или иные распределительные системы, при расчете которых, в первую очередь, важен учет потоков массы/энергии. По контрасту, в Информационных процессах, перенос массы/энергии не учитывается вовсе.
Игнорируя внутреннее устройство и энергетику процесса, кибернетическая модель представляет объект "черным ящиком", для которого известен только набор входных и выходных сигналов. Взамен рассмотрения потоков энергии, такая модель сосредоточивает внимание на "потоке управления".
Пусть сигнал о победе в сражении может быть подан любым из трех способов (или их комбинацией): выстрелом из стоящей на возвышении пушки, пуском красной ракеты или (в ночное время) костром на вершине холма. Энергетические затраты во всех случаях будут различны, но смысл заранее обусловленного сигнала - одинаков.
Более формально, Информационный процесс требует двух идентичных моделей (разделяемая модель) у Источника и Приемника, начальное состояние которых известно и идентично (тезаурус) и сигнала, позволяющего устранить возможное рассогласование (сообщение, синхропосылка, синхросигнал).
Понятие разделяемой модели неявно присутствует в любой модели коммуникации и означает, что стороны заранее договариваются об используемом алфавите, языке текста, его грамматике и любых иных подразумеваемых соглашениях ("культурный код", этикетные нормы и т.п.). Одна из проблем любого иностранца - незнание порядка и обычая, неявно разделяемых членами общины. Все замкнутые коллективы (близнецы, супруги, зимовщики) непременно создают свой мини-язык и набор мемов, известных только им и упрощающий коммуникацию внутри общины ("понимают друг друга с полуслова").
Удобной моделью коммуникации может служить игра в шахматы по переписке. Игроки не видят друг друга, у каждого своя собственная шахматная доска и они поочередно обмениваются только сделанными ходами. Очевидно, что само устройство шахматной доски, набор фигур, стартовая позиция и свод правил игры образуют тезаурус (константную часть), а набор ходов - синхросигналы (переменную часть) полного процесса коммуникации.
Игроки разделяют (совместно используют) модель шахматной доски и правила игры. Неважно, как и из чего сделаны фигуры, сам материал доски, ее цвет и размеры. Неважно, как именно передаются ходы - голубиной почтой или электрическим телеграфом. Никакие физические соображения не имеют отношения к игре, пока она ведется корректно.
Синхронизация начальных состояний моделей (игроки ставят фигуры в стартовую позицию) является обязательным общим условием любой коммуникации: шпионы сверяют часы; юристы уточняют термины; изучающий язык должен усвоить фонетику и грамматику; весы перед взвешиванием выводят "в нуль"; спортсмены занимают места на старте; секретные агенты договариваются о ключе и шифре и т.д.
Из сказанного следует, что можно отождествить Информационный процесс с процессом синхронизации двух моделей (общей разделяемой модели), принадлежащих Источнику и Приемнику.
В самом деле, для успеха коммуникации, изначально две идентичные модели должны находиться в том же самом начальном состоянии. В силу неких причин они оказываются рассогласованы. Поступающий сигнал позволяет вновь привести их в согласованное состояние (синхронизм).
Примером могут служить уже упомянутая игра в шахматы или корректировка артиллерийского огня. В любом следящем устройстве сигнал будет корректировать наведение на цель, что эквивалентно синхронизации состояний двух идентичных моделей - Источника и Приемника.
Для установления синхронизации необходимо выполнение трех условий:
1. Наличие функционально идентичных связанных систем (игроки в шахматы разделяют общую шахматную доску и набор правил игры - разделяемая модель).
2. Разделяемые модели обоих участников изначально синхронизированы между собой ("сверим часы", выбор общего шифра и секретного пароля для переписки, согласование прав и обязанностей сторон в юридическом документе и т.п.).
3. Сам процесс синхронизации выполняется путем отсылки сигналов, извещающих об изменении состояния одной из сторон. (шахматисты обмениваются ходами).
Использование модели означает, что сравниваемые системы не обязаны быть идентичными, а должны разделять только выбранные, важные для заданной цели (измерения) характерные качества.
Например, в экспериментах с бросанием монеты, существование Модели означает как предположение о свойствах объекта, так и ожидание определенного поведения. В опытах с бросанием монеты, понятие свойства предполагает "плоскую" монету, всегда выпадающую только лицевой (аверс) или обратной (реверс) стороной и никогда - на ребро. Предполагается, что рельеф лицевой и обратной сторон различен и различим. Предполагается, что подброшенная монета обязательно упадет, а не унесется со свистом в космическое пространство. Поведение предполагает случайность и равновероятность выпадения любой из сторон, и что различие рельефа аверса и реверса не оказывает влияния на исход опыта.
Модель не предполагает, что монета является подлинной, не имеет изъянов или имеет хождение. Модель не учитывает номинала монеты, ее вес, альбедо или электропроводность. Иными словами, Модель - это абстракция (существенных только для задающего вопрос) аспектов состояния и поведения объекта, не требующая ни реального существования объекта, ни фактического наличия у него данных свойств, ни даже совпадения реальных свойств объекта со свойствами модели.
Функциональная идентичность моделей не требует их физической идентичности.
Как пример функциональной идентичности можно привести синхронизацию часов по радиосигналу точного времени. "Ходики" с кукушкой и атомный эталон на изотопе цезия-133 внешне имеют немного общего, но оба разделяют ту же самую функциональную модель "часы, показывающее время с точностью до одной минуты". И в момент синхронизации состояние этих моделей (разделяемая модель) устанавливается идентичным.
Окончательно, под информацией понимается результат синхронизации состояний моделей Источника и Приемника.
Предложенный подход - отождествление Информации с результатом синхронизации, не вводит никаких новых сущностей, основан только на наблюдаемых характеристиках и дает более внятное представление о природе Информации.
Физический смысл энтропии
Информационная энтропия введена Шенноном в контексте передачи сообщений и потому может казаться связанной именно с обработкой текстов. На самом деле, эта характеристика применима к любой распределительной системе с древовидной структурой (наличием вариантов выбора в узлах дерева). По сути, всякий раз, когда с ростом размера системы число ее состояний растет экспоненциально ("комбинаторный взрыв") мы нуждаемся в логарифмической оценке, такой, как энтропия.
Решая задачу транспорта сообщений, Шеннон неявно пришел к двухкомпонентной модели. Можно сказать, сообщение представляется в виде смеси абсолютно несжимаемой ("жидкость") и абсолютно сжимаемой ("газ") компонент. При расчете потребной тары, достаточно учесть только количество несжимаемой компоненты ("количество информации"). Аналогичная двухкомпонентная модель может быть использована и для расчета пропускной способности. При этом, Информация и Шум рассматриваются как несмешивающиеся жидкости, совместно прокачивающиеся по тому же самому каналу. Чем выше доля шума, тем меньшая часть сечения канала (пропускная способность) доступна для информации и тем больше время передачи сообщения.
Таким образом, в задаче транспорта сообщений, энтропию можно рассматривать как "насыпную плотность" или "концентрацию" текста. Если частоты всех символов равны представлены все символы алфавита и кратности всех символов совпадают, то результирующая концентрация (энтропия) максимальна и равна единице. Если текст неоднороден - представлены не все символы алфавита и/или кратности их различны, то результирующая концентрация (энтропия) ниже предельной.
Если рассмотреть, например, процедуру взвешивания на рычажных весах, то килограмм сахарного песка может быть уравновешен килограммом золотого песка. Ни по каким своим характеристикам два этих товара не равноценны друг другу: золотой песок бессмысленно сыпать в чай, а сахарный - нести к ювелиру.
Но если требуется переслать и тот и другой посылкой с оплатой по весу, то в этом, и только в этом смысле они оказываются эквивалентны.
Иронично, но вычисленное по формулам "количество информации", к информации ни малейшего отношения не имеет. Оценки Хартли-Шеннона - это оценки платы за транспортировку сообщения, безотносительно к тому какая в нем содержится информация и содержится ли вообще: транспортировка дезинформации или шума, например, обойдется в ту же самую сумму.
Энтропия сообщения - это технический показатель его "насыпной плотности", "чистого веса", "нетто", позволяющий рассчитать предельное, минимально необходимое для транспортировки количество тары заданной вместимости, и не учитывающий ни природу товара, ни его ценность для получателя.
При транспортировке, для расчета потребной тары (пропускной способности канала связи) существенна только несжимаемая часть - энтропия, которая и будет выполнять роль меры.
Важно понимать, что выражения вида "энтропия - мера неопределенности" или "энтропия - мера беспорядка" не более, чем не имеющие смысла "маркетинговые уловки". И, тем более, энтропия никак не связана с информационным содержанием сообщения. Энтропия совершенно безразлична к порядку и соотношению своих составляющих, важна только их сумма. Шенноновская энтропия сообщения 0, 1, 2 ... N не изменится от любой, сколь угодно случайной перестановки ("перемешивания") символов последовательности. По критерию энтропии неразличимы любые анаграммы. Например, в парах "апельсин - спаниель" или "нерасторжимость - старорежимность" оба слова каждой пары имеют идентичную шенноновскую энтропию.
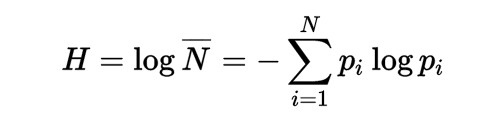
Можно, однако, взглянуть на формулу энтропии и по-иному.
Рассматривая распределительную систему (дерево), можно заметить, что число слагаемых под знаком суммы равно числу ветвей этого дерева, а один из сомножителей численно равен потоку ветви. Формально, второму (логарифмическому) сомножителю можно приписать смысл реакции ветви на протекающий поток (напора ветви).
Поскольку вероятность - нормированная величина, то произведение потока на напор (формально, площадь) будет иметь смысл относительной мощности ветви, а вся сумма - нормированной мощности (или коэффициента использования) дерева (распределительной системы).
|