Раздел 2. МИРЫ ИСАЕВА
1. ТИПЫ ЧИСЕЛ (МИРЫ ЧИСЕЛ)
Рассмотрим ряд натуральных чисел N, то есть чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, ... (и так - до бесконечности). Среди этих чисел есть так называемые простые числа (2, 3, 5, 7, 11, 13, ... - также до бесконечности), которые делятся (нацело) только на единицу и самих себя. Говоря о простых числах, мы будем обозначать их буквой Р (а не буквой N). Замечу, что о простых числах позже у нас будет совершенно особый разговор.
Основная теорема арифметики утверждает, что каждое натуральное число N, превосходящее единицу (N > 1), представляется единственным способом в виде:
N = P1^a × P2^b × P3^c × P4^d ×... × Pn^m, (1.1)
где P1, P2, P3, P4, ..., Pn - некие простые числа (располагаем их по возрастанию, все они не превосходят числа N);
a, b, c, d, ..., m - показатели степени (любые натуральные числа, большие нуля: 1, 2, 3, 4, 5, 6, 7, ...).
Представление (запись) натурального числа N в виде (1.1) называется каноническим разложением числа N (на простые сомножители) или факторизацией числа N. Например: 20 = 2^2∙5 (заметим, что 5^1 = 5, то есть любое число в 1-й степени равно самому числу); 36 = 2^2 ∙ 3^2; 42 = 2∙3∙7; 84 = 2^2 ∙3∙7; 132 = 2^2 ∙3∙11. Поскольку, например, 261360 = 2^4 ∙ 3^3 ∙ 5^1 ∙ 11^2, то никакой другой набор простых чисел Р никогда не даст нам числа 261360, то есть следует ясно понимать, что факторизация любого числа N имеет своим итогом единственно возможный результат!
Поиск показателей степени a, b, c, ..., d при факторизации - задача далеко непростая. В серьезной компьютерной программе Mathcad 2000, ориентированной на решение математических задач, существует даже специальная команда (Factor) для автоматического поиска этих показателей, то есть для факторизации числа N (вплоть до числа N порядка 10^15?). У произвольно взятого достаточно большого числа N бывает совсем не просто найти его каноническое разложение даже с помощью компьютера. И даже определить является ли данное большое число N простым числом или составным - порой бывает очень трудно.
Таким образом, начиная с N = 2, любое натуральное число N, можно представить (причем единственным способом) в виде некого произведения простых чисел (например, 261360 = 2∙2∙2∙2∙3∙3∙3∙5∙11∙11). То есть в мире натуральных чисел простые числа являются теми фундаментальными кирпичиками ('атомами'), из которых строится бесконечное множество всех прочих чисел (подобно тому, как из небольшого числа атомов 'таблицы Менделеева' строится огромное количество всевозможных молекул реального мира).
Одним из ключевых понятий виртуальной космологии является понятие о типе натурального числа.
Тип числа - это количество всех целых делителей натурального числа N (включая 1 и само число N).
Тип числа мы будем обозначать буквой Т. Например, у числа N = 20 всего шесть делителей: 1, 2, 4, 5, 10, 20 поэтому его тип Т = 6. Заметим, что первое натуральное число N = 0 имеет бесконечно большой тип (Т устремляется к числу 'бесконечность'), поскольку нуль делится на любое число (кроме нуля). Мы будем полагать, что число 'бесконечность' (строго говоря, это не число), 'делится' на все натуральные числа N (начиная с единицы) поэтому первое натуральное число N = 0, в некотором смысле, 'смыкается' (в части своего типа Т) с числом 'бесконечность'.
Число N = 1 (единица) является единственным особым числом, у которого тип равен единице (Т = 1).
Ясно, что у любого простого числа Т = 2 (и таких чисел бесконечно много).
Каноническое разложение числа N - это своеобразное 'досье' ('паспорт'), из которого можно извлечь массу любопытных сведений о числе N. Так, зная каноническое разложение числа N [его разложение согласно формуле (1.1)], можно вычислить тип (Т) данного числа N:
T = (a+1)(b+1)(c+1)(d +1)... (m+1). (1.2)
Общеизвестную формулу (1.2) мы будем называть каноническим типом числа N, подчеркивая тем самым, что тип Т данного числа N мы нашли по его каноническому разложению. Например, для числа N = 261360 = 2^4 ∙ 3^3 ∙ 5^1 ∙ 11^2 мы получим канонический тип Т = (4+1)(3+1)(1+1)(2+1) = 120, то есть указанное число N имеет ровно 120 целых делителей (убедитесь в этом сами, найдя с помощью компьютера все делители данного числа).
Малые делители
Если все делители любого числа N расположить по возрастанию, то, перебрав первую их половину (малые делители), мы обнаружим, что остальные (большие делители) равны частному от деления числа N на один из малых делителей. Так, у числа N = 20 есть три малых делителя - 1, 2, 4, и три больших делителя - 5, 10, 20 (которые равны отношениям: 20/4, 20/2, 20/1). Проверка: 20 = 2^2∙5^1, значит Т = (2+1)(1+1) = 6 - количество всех делителей.
Таким образом, определение типа числа N 'в лоб' (когда мы, скажем, не знаем его канонического разложения) сводится к поиску малых делителей числа N, причем на отрезке [1; N^0,5], где выражение N^0,5 означает корень квадратный из числа N (данный корень ещё не раз нам встретится в рамках виртуальной космологии). Ведь если число N > 1 и равно произведению двух натуральных чисел, то, по крайней мере, одно из них не больше, чем N^0,5 - это заметил ещё Фибоначчи. Таким образом, малые делители - это также некий 'паспорт' числа N, с важнейшей информацией о нём (наравне с каноническим разложением числа N).
Средний тип числа (формула Дирихле)
В натуральном ряде появление различных типов (чисел с различными типами) носит псевдослучайный характер, то есть на практике, вообще говоря, невозможно предсказать какой тип будет у следующего числа N. Очевидно только одно - чем дальше мы уходим от единицы (N = 1), тем большие типы могут появиться, причем наряду с ними неизбежно будут появляться числа и с самыми малыми типами Т = 2, 3, 4, ... .
Любому натуральному числу N помимо типа Т мы будем также приписывать средний тип (Тs), который равен среднему арифметическому всех типов у чисел от 1 до N включительно:
Ts = (Т1 + Т2 + Т3 + T4 + ... + Тn)/N . (1.3)
Несмотря на беспорядочные колебания типов Т, средний тип Ts ведет себя на удивление спокойно. Закон роста параметра Ts впервые установил немецкий математик Петер Густав Лежён Дирихле (1805-1859), поэтому этот важнейший для нас закон мы будем называть формулой Дирихле:
Ts = lnN + (2×C -1) + 'эпсилон', (1.4)
где С = 0,577 215 664 901 532... - постоянная Эйлера-Маскерони (или постоянная Эйлера), а параметр 'эпсилон' устремляется к нулю, когда число N неограниченно возрастает. В начале натурального ряда реальный средний тип (Tsr) превосходит (теоретическое) значение Ts, но, начиная с числа N = 47, некоторые реальные значения среднего типа могут быть и меньше Ts, то есть начинаются хаотичные колебания реального среднего типа 'вокруг' значений Ts. При этом относительная погрешность (ОП) формулы Дирихле быстро убывает, так, считая 'эпсилон' равным нулю, я оценил модуль ОП = (Tsr - Ts)/Ts формулы Дирихле (1.4) следующим эмпирическим выражением:
abs(ОП) < 1/N^w, где w = 'пи'^2/12 = 0,8225. (1.5)
Математическая константа С определяется как предел разности между частичной суммой гармонического ряда и натуральным логарифмом числа N (полагаем, что число N устремляется к бесконечности):
C = lim[( 1/1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + ... + 1/N) - lnN]. (1.6)
Константа С введена в 1735 году Леонардом Эйлером. Итальянский математик Лоренцо Маскерони в 1790 году вычислил 32 знака константы и предложил её современное обозначение (греческой буквой 'гамма'). Однако арифметическая природа числа С не изучена: до сих пор не выявлено, является ли это число С рациональным. Однако теория цепных дробей показывает, что если постоянная С - рациональная дробь, то её знаменатель больше 10^242080.
Рефлекция 1.1. [Заметим, что константа С = 0,577... (весьма 'востребованная' в теории чисел!) близка к пресловутому 'золотому сечению' (0,618), а в конце Большого отрезка (то есть при N = 8∙10^60 эви) средний тип равен Ts = 140,39, что близко к обратному значению постоянной тонкой структуры: 1/ПТС = 137.
Забегая вперед в части некоторых параметров Большого отрезка, скажу, что в его конце у отдельных чисел N тип Т может достигать почти триллиона (целых делителей)! Поэтому небольшой средний тип Ts = 140,39 в конце Большого отрезка может иметь лишь единственное объяснение - натуральный ряд отдает предпочтение числам с... малыми типами Т: у подавляющего большинства чисел количество делителей невелико. Например, простых чисел (с наименьшим типом Т = 2) на Большом отрезке около 7×10^58 (штук), что составляет примерно 0,7%. И это весьма солидная доля, ведь в среднем на один мир должно приходиться 10^61/807430 = 1,2×10^55 чисел или 0,00012% от всех натуральных чисел Большого отрезка.
Таким образом, мир чисел как бы копирует (отражает) один из фундаментальных законов реального (физического) мира: в природе малые особи более распространены, чем крупные, где под словом 'особи' следует понимать не только биологические объекты, но и самые разнообразные объекты неживой материи.]
Миры чисел (миры Исаева)
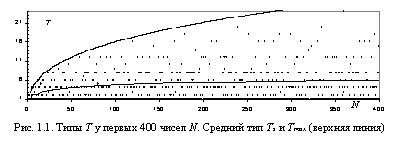
На рис. 1.1 точками показаны типы Т (их числовые значения) у первых 400 натуральных чисел N, и эти типы, словно воробьи на проводах, 'сидят' на разных уровнях, то есть принадлежат к разным типам. Но если воробей может перелететь на другой провод (уровень), то числа N каждого типа образуют некий замкнутый мир со своими неповторимыми законами (в чем нетрудно убедиться с помощью компьютера). Поэтому в виртуальной космологии иногда бывает удобнее говорить о мирах, которые объединяют числа с одинаковым типом. Так, все простые числа (с типом Т = 2) образуют мир 'номер 2', а мир 'номер 3' образуют числа с относительно редким типом Т = 3; миры 'номер 4' и 'номер 8' - довольно 'густонаселенные' (чисел с Т = 4 и Т = 8 довольно много) и т. д.
Миры возникают далеко не по возрастанию их номеров, приведем самые первые миры (типы первых 17-ти натуральных чисел): 1, 2, 3, 4, 6, 5, 8, 9, 10, 12, 7, 16, 15, 18, 14, 20, 24.
Рефлекция 1.2. [Если вспомнить про эви-конвертацию, то первые 10^43 натуральных чисел N можно воспринимать как временной интервал в одну секунду. За это время в натуральном ряде успевает 'промелькнуть' около 105 разных миров - примерно столько разных типов Т содержится на отрезке [1; 10^43]. В масштабе нашего (человеческого) времени в любое мгновение существуют как бы одновременно 'параллельные' миры - это те несколько миров (сколько - не совсем ясно), которые повторяются чаще всего, а высокая частота 'мельканий' делает их 'доступными' для нас (прочие миры мы просто не успеваем заметить - так рождаются 'скрытые' миры). Возможно, суть данной 'безумной' идеи теперь понятна читателю. Похоже, здесь есть место для полета фантазии...]
Итак, мы будем говорить, что все натуральные числа с одинаковым типом Т образуют мир 'номер Т'. Просто хотя бы потому, что иногда удобнее (разумеется, на вкус автора) говорить именно о мирах, а не о типах.
Все миры можно разделить на две существенно разные группы:
- Редкие (нечетные) миры - в них числа N имеют нечетный тип Т.
- Частые (четные) миры - в них числа N имеют четный тип Т.
Редкие миры образуют числа вида N = i^2, где i = 1, 2, 3, 4,... (натуральный ряд). Первые числа из редких миров: N = 1, 4, 9, 16, 25, 36, 49, 64, ... . Ясно, что доля таких чисел в натуральном ряде быстро убывает (по закону квадратной параболы). У всех указанных чисел N последний малый делитель равен первому большому делителю, поэтому количество больших делителей всегда будет на единицу меньше, чем малых - так возникает нечетный тип Т. Например, число N = 36 имеет малые делители: 1, 2, 3, 4, 6, значит, его большие делители будут такими: 36/6 = 6 (что повторяет последний малый делитель), 36/4 = 9, 36/3 = 12, 36/2 = 18, 36/1= 36. Таким образом, получаем, что у числа N = 36 = 6^2 тип равен нечетному числу Т = 7.
Лидеры миров
При движении вдоль натурального ряда у некоторого числа N впервые появляется тип Т. Такое число N мы будем называть лидером мира Т. Можно сказать, что лидер 'открывает' данный мир Т. Ясно, что лидеры частых миров (ЛЧМ) и лидеры редких миров (ЛРМ) - это бесконечные ряды натуральных чисел, вот первые из них:
ЛЧМ: N = 2, 6, 12, 24, 48, 60, 120, 180, 192, 240, 360, 720, 840, 960, ...
ЛРМ: N = 4, 16, 36, 64, 144, 576, 900, 1024, 1296, 3600, 4096, 5184, 9216, ...
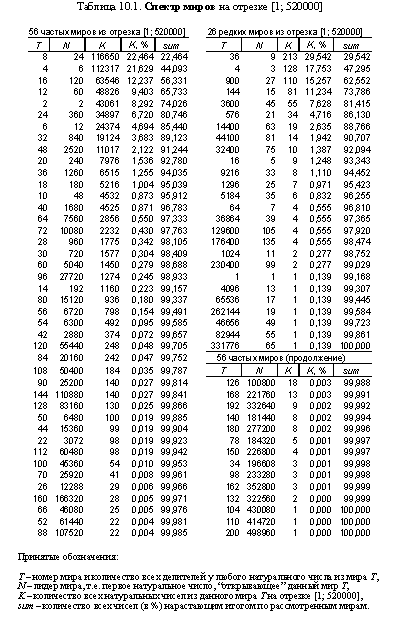
На рис. 1.2 показаны типы (Т) у лидеров (N) первых 82-х миров, появившихся на рабочем отрезке [1; 520000].
Ещё в начале 2002 г. мне удалось найти на Большом отрезке (предположительно) все 120000 ЛРМ. А вот ЛЧМ я смог найти только на отрезке [1; 10^32], где оказалось 22164 ЛЧМ. Экстраполируя этот результат, я получил такую оценку: на Большом отрезке, вероятно, находится около 687430 ЛЧМ (то есть в 5,7 раз больше, чем ЛРМ, где 5,7 - воплощение 'магии' числа 7?).
Любопытен следующий вопрос: в какой диапазон значений чаще всего попадают типы Т лидеров (ЛЧМ и ЛРМ) в пределах Большого отрезка? Вероятно, эти диапазоны таковы:
- для ЛЧМ - это Т = 10^8...10^9,
- для ЛРМ - это Т = 10^7...10^9.
Итак, мы ввели понятие 'лидер' - это некое особое число N (с особым типом Т). Если для всех найденных лидеров построить график T = f(N) в логарифмических осях (см. рис. 1.2), то на таком графике все точки (все значения Т у лидеров N) окажутся в расширяющимся (из начала координат) коридоре, напоминающем по своему очертанию... хвост кометы (в частых и редких мирах - свой 'хвост' лидеров, то есть мы имеем два 'хвоста', которые почти перекрывают друг друга на графике). Указанный 'хвост' на графике T = f(N) можно мысленно очертить некой верхней и нижней линией (границей) - так мы приходим к понятию о верхних и нижних лидерах (в частых и редких мирах).
Нижние лидеры - это лидеры N с такими типами Т, меньше которых в дальнейшем быть не может. На упомянутом графике T = f(N) именно через типы Т (точки на графике) нижних лидеров проходит нижняя воображаемая линия 'хвоста'. Нетрудно убедиться, что нижние лидеры в редких мирах - это лидеры так называемых простых миров, у которых тип равен простому числу Т = 2, 3, 5, 7, 11, 13, 17, 19, ... . А нижние лидеры в частых мирах - это лидеры так называемых удвоенных миров, у которых тип равен удвоенному простому числу Т = 4, 6, 10, 14, 22, 26, 34, ... . Нижний лидер N в частых и редких имеет следующий вид (соответственно):
N = 2^(T/2 - 1) ×3 и N = 2^(T - 1). (1.7)
Заметим, что мир 'номер 8' (его лидер N = 24) отличает некая аномалия: тип Т = 8 не является удвоенным миром, однако первая из формул (1.7) - все равно срабатывает (для Т = 8 проявляется... 'магия' числа 7?).
Нижнюю воображаемую границу 'хвоста' на графике T = f(N) можно описать следующими формулами (для частых и редких миров соответственно):
Tmin = 2×ln(N/3)/ln2 + 2 и Tmin = lnN/ln2 + 1. (1.8)
Нижняя граница 'хвоста' характеризуется тем, что с ростом числа N у любого нового ЛЧМ (ЛРМ) его тип Т будет никак не меньше Tmin.
К концу Большого отрезка набирается совсем немного нижних лидеров: в частых мирах - 46 штук (Tmin = 398), а в редких мирах - 47 штук (Tmin = 199). Это означает, что на Большом отрезке в частых мирах появятся все (без пропусков!) чётные типы Т = 2, 4, 6, ..., 398, а в редких мирах - нечётные типы Т = 1, 3, 5, ..., 199. А все большие типы, скажем, в редких мирах будут появляться со средней вероятностью всего лишь порядка 10^-6, поскольку верхняя граница 'флуктуаций' ЛРМ к концу Большого отрезка вырастет до Tmax = 8×10^10 (см. ниже), а всего появится 120000 нечётных миров.
Верхние лидеры образуют верхнюю воображаемую границу 'хвоста' на графике T = f(N) для лидеров, которая хорошо угадывается на рис. 1.2. И для частых, и для редких миров можно сформулировать следующее определение: если у лидера N его тип Т больше ранее появившихся типов, то такой лидер мы будем называть верхним лидером. Таковыми не являются (см. выше ряды ЛЧМ и ЛРМ):
- среди ЛЧМ - это N = 192, 960, ...;
- среди ЛРМ - это N = 64, 1024, 1296, 4096, 5184, 9216, ... .
Очевидно, что с ростом N верхние лидеры будут встречаться всё реже (на рис. 1.2 этого не видно, так как шкала логарифмическая). По моей оценке на Большом отрезке в редких мирах набирается 270 верхних лидера, а в частых мирах, вероятно, около 748 верхних лидеров.
Надо ясно понимать, что старший (наибольший) верхний лидер на отрезке [1; N] - это натуральное число, у которого максимальное количество делителей (из всех чисел данного отрезка). Например, у верхнего лидера N = 3600 тип Т = 45 и это значит, что на отрезке [1; 3600] ни одно число (из редких миров), кроме N = 3600, не имеет так много делителей (45 делителей). Таким образом, верхние лидеры - это весьма интересные числа в рамках виртуальной космологии (бесконечную последовательность которых, вероятно, невозможно задать никакой точной формулой?).
Максимально возможный тип (Tmax) на отрезке [1; N]. Беря за основу типы T у верхних лидеров N, хотелось бы построить некую линию Tmax = f(N), 'огибающую' сверху все типы Т (все точки на рис. 1.2). Однако далее мы сможем указать лишь функцию, 'вокруг' ('вдоль') которой расположены реальные значения Tmax.
Tmax в редких мирах
Как я уже говорил, ещё в начале 2002 г. мне удалось найти на Большом отрезке (предположительно) все 120000 лидеров редких миров (ЛРМ). Из них верхними лидерами оказались только 270 чисел. Для примера ниже приведены канонические разложения трех наибольших (последних) на Большом отрезке верхних лидеров N (из 270-ти):
N = 2^12×3^4×5^4×7^4×(11×13×17×19×23×29×31×37×41×43×47×53×59×61×67×71)^2 = 3,51×10^60;
N = 2^12×3^8×5^4×7^2×(11×13×17×19×23×29×31×37×41×43×47×53×59×61×67×71)^2 = 5,81×10^60;
N = 2^10×3^6×5^4×7^4×(11×13×17×19×23×29×31×37×41×43×47×53×59×61×67×71)^2 = 7,91×10^60;
Зная канонические разложения чисел N, мы находим их типы Т (соответственно) по формуле (1.2):
Т = (12 + 1)(4 + 1)(4 + 1)(4 + 1)(2 + 1)(2 + 1)(2 + 1)...(2 + 1) = 69 950 921 625 = 7,0×10^10;
Т = 75 546 995 355 = 7,6×10^10;
Т = 82 864 937 925 = 8,3×10^10.
В рамках виртуальной космологии мы договоримся называть функцию Y = f(X) - лже-функцией, если она имеет вид (близка к виду) Y = exp[a×(lnX)^b], где a и b - некие эмпирические коэффициенты, скажем, 'снятые' с линии тренда на графике Y = f(X). Причём этот график (состоящий из дискретных точек-значений) на самом деле может вообще не иметь в качестве своего описания ни одну из известных в математике непрерывных функцией - именно поэтому я и выбрал название 'лже-функция' (чтобы сразу признаться читателю в неком 'обмане').
Итак, знание 270 верхних лидеров N у редких миров Т, то есть наличие графика T = f(N), состоящего из 270-ти точек-значений (типов Т) позволяет определить лже-функцию следующего вида:
Tmax/Ts = exp[a×(lnN)^b] , (1.9)
где Ts - средний тип (найденный по формуле Дирихле) у числа N, для которого находим Tmax, причем:
a = 0,2465; b = 0,9028 и abs(ОП) = 12% на отрезке [24; 10^20] (это Малый отрезок - см. 'Исходные понятия...');
a = 0,3031; b = 0,8493 и abs (ОП) = 9% на отрезке [10^20; 10^61] (то есть до конца Большого отрезка).
Tmax в частых мирах (i-триллион)
Как я уже говорил, ещё в начале 2002 г. мне удалось найти (предположительно) все лидеры частых миров (ЛЧМ), но только на отрезке [1; 10^32], где оказалось 22164 ЛЧМ. Экстраполируя этот результат, я получил такую оценку: на Большом отрезке, вероятно, находится около 687430 ЛЧМ.
Ещё мне удалось найти отдельные числа N, расположенные в конце Большого отрезка, и имеющие очень большое количество делителей (имеющие большой тип Т). Будем считать, что это и есть верхние лидеры частых миров, а их канонические разложения и типы Т (соответственно) приведены ниже:
N = 2^10∙3^6∙5^4∙7^3∙11^2∙13^2∙17^2∙M = 7,44∙10^60;
N = 2^10∙3^5∙5^3∙7^2∙11^2∙13^2∙17^2∙M∙137 = 9,28∙10^60;
где M = 19∙23∙29∙31∙37∙41∙43∙47∙53∙59∙61∙67∙71∙73∙79∙83∙89∙97∙101∙103∙107∙109∙113∙127∙131;
T = 697 596 641 280 = 7,0×10^11;
T = 717 527 973 888 = 7,17×10^11;
Самая обыкновенная (линейная) интерполяция между двумя указанными числами N показывает, что в конце Большого отрезка (то есть при N = 8∙10^60) мы получим Т = 7,03∙10^11.
Рефлекция 1.3. [Как мы видим, в конце Большого отрезка наибольший (последний) верхний лидер N 'строится' с помощью первых 32-33 простых чисел (2, 3, 5, 7, ..., 131, 137), которые идут подряд (без пропусков) в каноническом разложении данного числа N (и каждое из простых чисел возведено в некую степень: 10, 6, 4, 3, 2, 2, 2, 1, 1, 1, ..., 1).
Указанное количество (32-33) простых чисел, вероятно, находит своё 'отражение' в реальном мире, где эти числа (или близкие к ним числа) играют фундаментальную роль. Вот лишь некоторые примеры:
32∙2 кодона (и 46 хромосом) в структуре ДНК; 32 зуба у человека; 27 костей в кисти руки человека (и это очень совершенный орган!); 26 костей в стопе ноги человека; 33-34 позвонка в позвоночнике человека; до 33 букв содержат большинство алфавитов в мире; 33 основных языка на планете; 33 значимых религии на планете; 33 термина указывают темп в музыке; 32 краски на палитре художника - это (ещё более-менее разумный) максимум красок;...
32 варианта расположения атомов вокруг узла решетки (см. кристаллографию); 29 скоплений галактик в крупнейшем из сверхскоплений; 39 спутников у Юпитера (это максимум в солнечной системе);...]
Лже-функция в частых мирах также выражается формулой (1.9), но уже при других параметрах:
a = 0,2710; b = 0,9028 и abs(ОП) = 9% на отрезке [24; 10^20] (то есть в пределах Малого отрезка);
a = 0,3197; b = 0,8588 и abs(ОП) = 5% на отрезке [10^20; 10^61] (то есть до конца Большого отрезка).
Итак, с ростом числа N его максимально возможный тип Тmax (ясно, что он реализуется в частых мирах) - увеличивается, причём существует ограничение на значение Tmax (для конкретного числа N). В первом приближении на Большом отрезке можно использовать совсем простую (и чисто эмпирическую) лже-функцию:
Tmax = exp[(lnN)^0,6692]. (1.10)
На рис. 1.1 верхняя граница типов (Tmax) изображена пунктирной линией. Согласно всем моим оценкам (приведенным выше), в конце Большого отрезка, максимально возможный тип равен Tmax = 7∙10^11, и это число впредь мы будем называть i-триллионом (триллионом Исаева). Пусть это не очень скромно, но зато сразу ясно, о чём именно идет речь (7∙10^11 - это почти триллион, то есть почти 10^12), и сразу ясно, что автор придает огромное значение найденному важнейшему параметру Большого отрезка: у гигантских натуральных чисел (чья запись включает в себя 61 цифру!, ведь это числа N порядка 10^61) будет почти триллион целых делителей. Если каждый делитель представить в виде одного миллиметра, то триллион делителей растянутся на один... миллион километров!
Рефлекция 1.4. [В конце Большого отрезка (в современную нам эпоху) Tmax частых миров примерно в 8 раз превосходит Tmax редких миров (очередная 'магия' числа 7). Ещё мы получаем очень важное в рамках виртуальной космологии соотношение: Tmax/Ts = 5∙10^9, где Ts = 140,39 - средний арифметический тип всех натуральных чисел на Большом отрезке. При этом заметим, что в реальной космологии одним из основных параметров нашей Вселенной является отношение числа фотонов к числу барионов: от 10^9 до 3,33∙10^9.
Найденные мною многочисленные 'отражения' i-триллиона (Tmax = 7∙10^11) в реальном физическом мире - собраны в последнем (пока, условно говоря, - в 100-м) разделе моей книги в главе 'Триллион Исаева']
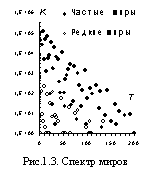
Спектр миров - это картина распределения всех миров (Т) по количеству (K) натуральных чисел, в них содержащихся (на данном конкретном отрезке). Так, спектр миров моего рабочего отрезка [1; 520000] можно представить в графическом виде (рис. 1.3) или в виде таблицы 1.1. Рис. 1.3 наглядно показывает, что с ростом типа Т максимально возможные количества (Kmax) чисел в данных мирах экспоненциально убывают. А из табл. 1.1 хорошо видно, что семь ('магия' числа 7) самых 'густонаселенных' частых (редких) миров содержат 85,44% (88,77 %) всех натуральных чисел рабочего отрезка (кстати, 'шапка' табл. 1.1 в части редких миров содержит ошибку: в 'шапке' перепутаны местами буквы T и N).
Миры-фантомы
Нетрудно убедиться, что, скажем, на отрезке [1; 360] не появляются миры с номерами (с типом Т) 11, 13, 17, 19, 21, 22, 23 - эти миры мы назовем мирами-фантомами. Поскольку совершенно очевидно, что при увеличении правой границы отрезка (N > 360) миры-фантомы рано или поздно появятся (каждый - в своё 'время'), перестав быть фантомами (фантомами станут другие миры). Ведь номера всех миров (типы Т у всех натуральных чисел N) также образуют бесконечный натуральный ряд (начинающийся с единицы).
На произвольном отрезке [1; N] количество миров-фантомов Кф (как в частых, так и в редких мирах) устремляется к значению максимально возможного типа Tmax (в соответствующих мирах). При этом, разумеется, всегда будет выполняться условие: Кф < Tmax.