Содержание статьи:
1. Краткие сведения об эквивалентных и антиподно − эквивалентных числовых множествах.
2. Рефлективно − числовые матрицы, как математическая основа построения постоянно действующих во времени календарей.
2.1. Анализ внутренней структуры календаря.
2.2. Анализ внешней структуры календаря.
3. Структурно − функциональный анализ квадратного уравнения Хˆ 2 ± РХ - С = 0. ∗)
∗) примечание: символ ˆ − это символ степени; например: 2ˆ 2 = 4.
1. Краткие сведения об эквивалентных и антиподно − эквивалентных числовых множествах.
Первое, с чем приходится сталкиваться человеку, приступившему к изучению Математики, с её первичными, неопределёнными понятиями. К числу таковых относится и понятие "множество". Этому понятию нельзя дать формального определения, которое не сводилось бы просто к замене слова "множество" его синонимами "совокупность", "набор элементов" и т. п. Множества можно составлять на основе самых разнообразных признаков из самых различных материальных объектов или абстрактных понятий (числа, геометрические фигуры, символы и т. п.), которые называют элементами множества. При наличии двух или нескольких множеств, между ними можно установить соответствие, исходя из правила, по которому для каждого элемента одного множества выбирается определённый элемент или подмножество элементов другого множества. А уже на основе понятия соответствия между множествами, вводится понятие отображение множеств. Отображение множеств, друг в друга или друг на друга, может быть однозначным и неоднозначным. При взаимно однозначном отображении, например, множества А на множество В, разным элементам множества А соответствуют различные элементы множества В. Такие множества А и В называются эквивалентными. Эквивалентность множеств записывается с помощью знака ∼ : А ∼ В.
Укажем так же ещё на то, что множество по количеству входящих в него элементов может быть конечным или бесконечным. Так, множество, эквивалентное отрезку натурального ряда чисел (натуральным рядом называется числовая последовательность, начинающаяся с 1 −цы и продолжающаяся в бесконечность: 1; 2; 3; 4; 5; 6; 7; . . . . ∞), называется конечным множеством; пустое множество также считается конечным множеством. Иными словами: коечное множество (если оно не пусто) − это множество, элементы которого можно "пересчитывать" за конечное число шагов и т. д., затрачивая при этом соответствующий конечный интервал времени. Если при этом каждому элементу конечного множества А присвоить кокой − либо номер от 1 −цы до некоторого натурального числа так, чтобы все числа от 1 −цы до n были использованы и различные элементы множества получили различные номера, то число n укажет число элементов данного множества А, характеризующее мощность множества.
Предположим, что у нас имеется конечное число предметов, например, яблок и нам требуется определить их количество. Возникает вопрос: сколькими способами это можно сделать? Это можно сделать тремя способами. В первом случае, все яблоки можно выложить на столе в ряд, друг за другом, и, поставив в соответствие каждому из них определённое число из натурального ряда чисел (N), начиная с 1 −цы, мы определим их количество. Во втором случае, всё конечное множество яблок можно разбить на несколько эквивалентных групп, т. е. с одинаковым количеством яблок в каждой группе, а затем произвести последовательное сложение групп или же, заменяя операцию сложения − умножением количества эквивалентных групп на количества входящих в одну группу элементов (яблок).
Первый вариант (см. рис. 1) является истинно эквивалентным, ибо для всех элементов (чисел),

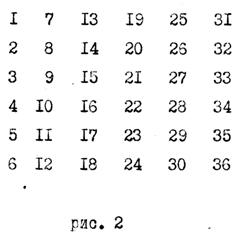
Такое различие обоих вариантов не сказывается на относительном (конструктивном) расположении самих элементов (чисел) в группах по отношению друг друга. То есть, оба варианты едины (эквивалентны) по схеме построения и различны по форме записи числовых последовательностей в группах. В последующем, подобную схему построения числовых групп, будем именовать эквивалентной или псевдо − эквивалентной, числовой матрицей.
Рассмотренный выше пример с взаимным расположением чисел по схеме эквивалентной (пс.экв−ой) матрицы показывает, что при её построении можно использовать сразу или несколько одинаковых числовых последовательностей (натуральных рядов чисел, используя свойство рефлективности), или же использовать только одну числовую последовательность (соответствующее конечное множество из натурального ряда чисел), вводя для этого случая соответствующий алгоритм её построения. Такая возможность обусловлена тем, что натуральный ряд чисел (N) делится на два равновеликих подмножества: нечётных (1 + 2К) и чётных (2 + 2К) чисел. Задавая числовому оператору К целочисленные значения, начиная с нуля, мы получим вышеназванные подмножества − числовые последовательности в виде псевдо − эквивалентной числовой матрицы:

В этой числовой матрице, имеющей алгоритм построения 2, слева от знака равенства, симметрично относительно друг друга записаны общие формулы подмножеств, а справа сами подмножества. Эта схема записи типична для пс.экв−ой числовой матрицы и в общем случае может быть построена с любым, наперёд заданным числовым алгоритмом, находящимся с конечным множеством А в кратных отношениях. При этом общее количество пс.экв−х строк такой матрицы не превышает значение алгоритма. Так, например, для ранее рассмотренного примера, где А(36), пс.экв−ая числовая матрица (см. рис. 2) была построена в соответствии с алгоритмом 6. Вместе с формулами эта матрица запишется в следующем виде:

В данном примере число строк равно числу групп (столбцов) и такая матрица называется квадратной. В случае отсутствия равенства, матрица будет прямоугольная. В качестве примера рассмотрим числовое множество А(36). Для нахождения общего количества вариантов представления данного множества в виде пс.экв−х (т. е. псевдо − эквивалентных) числовых матриц, сначала представим число 36 в виде произведения простых чисел и единицы: 1 • 2 • 2 • 3 • 3. После этого составим варианты кратности числа 36 его сомножителям и их комбинациям. Так, число 36 кратно следующим числам: 1; 2: 3; 4; 6; 9; 12; 18; 36. Следовательно, общее количество пс.экв−х числовых матриц будет равно 9 −ти. Ниже приводятся числовые матрицы, соответствующие этим девяти вариантам:



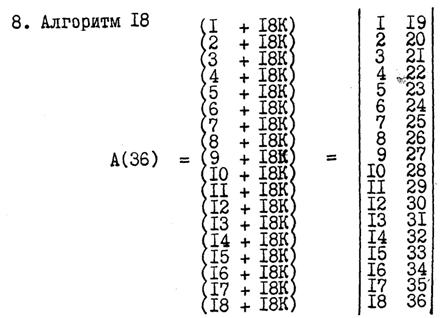
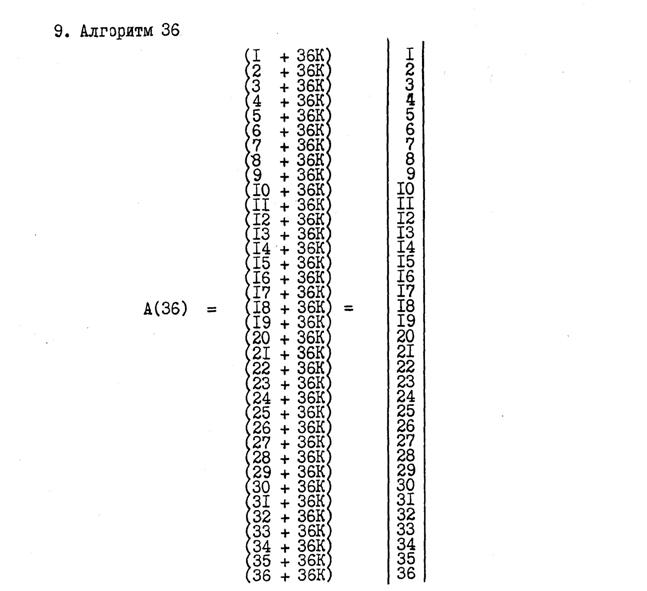
Вышеприведённые 9 вариантов пс.экв−х числовых матриц, для конечного множества А(36), были построены в соответствии с наперёд заданным числовым оператором К, представляющим числовую последовательность 0; 1; 2; 3; 4; . . . . и т. д. В зависимости от конструктивных параметров матриц общее количество составляющих эту числовую последовательность цифр может быть разное. В общем же случае следует отметить, что с ростом алгоритма построения матриц, числовой оператор К имеет тенденцию к уменьшению от максимума до минимума.
Исходя из сказанного представляется, что эквивалентные и пс.экв−е числовые матрицы, по характеру расположения в них эквивалентных и пс.экв−х элементов (чисел) относительно друг друга, можно подразделять на построчные (горизонтальные), прямоугольные, квадратные и вертикальные. В соответствии с этим саму эквивалентность (и пс.экв−ть) будем характеризовать как построчную, прямоугольную, квадратную и вертикальную.
Эти конструктивные признаки эквивалентных и пс.экв−х числовых матриц позволяют ввести понятие компактной записи (представления) числовых множеств. Очевидно, что из четырёх видов самой компактной будет запись числовой, конечной последовательности, в виде соответствующей матрицы по схеме "квадратной" эквивалентности (пс.экв−ти). В качестве таковой, из рассмотренных является матрица А (36) с алгоритмом построения равным 6 −ти.
Если мы теперь введём соответствующие обозначения, то сможем записать общую формулу пс.экв−х (в том числе и эквивалентных) вариантов числовых матриц. Так, обозначая через в − алгоритм построения матрицы; М − символ числовой матрицы; а − числовой инвариант; N − конечное числовое множество; с − показатель степени матрицы (в общем случае представляет ту же числовую последовательность, что и числовой оператор К, или может приравниваться одному из значений К); р = Q/q − показатель рефлективности числовой матрицы {здесь: Q − общее количество групп − столбцов в матрице; q − общее количество пс.экв−х столбцов в одной рефлективной группе}; Λ− количество строк в пс.экв−ой матрице, мы получим следующую формулу:
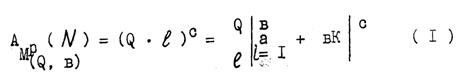
В эту формулу входит показатель рефлективности пс.экв−ой числовой матрицы р , который предопределяет взаимно однозначное соответствие между числовыми элементами как в плане количественном, так и в плане качественном − характере написания числового элемента. К этому добавляется ещё и условие местоположения рефлективных чисел в рефлективных группах.
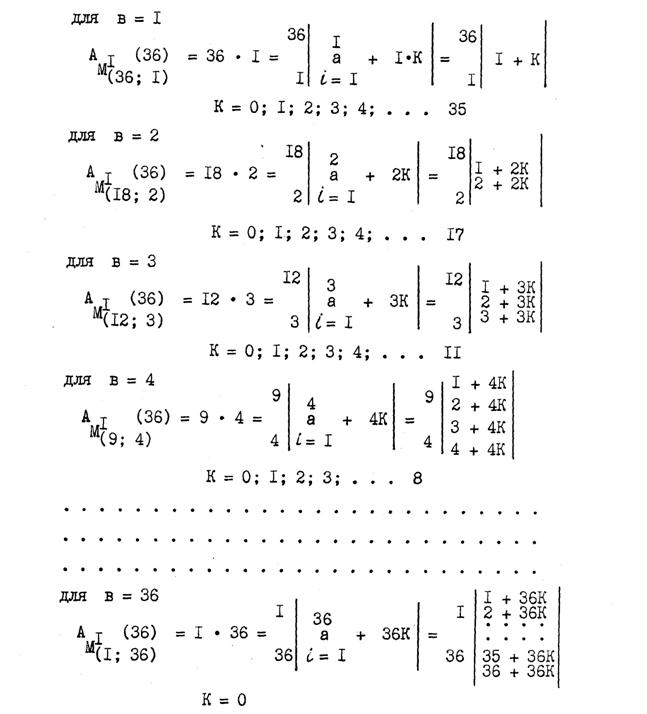
В качестве примера, ниже приводятся два варианта пс.экв−ой числовой матрицы конечного множества А(78). Обе матрицы выполнены по алгоритму в = 13. В соответствии с этим алгоритмом, общее количество столбцов в матрице будет равно: Q = N/в = 78/13 = 6. Полагая количество групп q в одной рефлективной группе, в одном случае 2, а во втором 3, мы найдём, что показатель рефлективности первой матрицы будет равен: р(1) = Q/q(1) = 6/2 = 3; для второй р(2) = Q/q(2) = 6/3 = 2. Обе матрицы, в соответствии с найденными значениями р(1) и р(2), приводятся ниже:
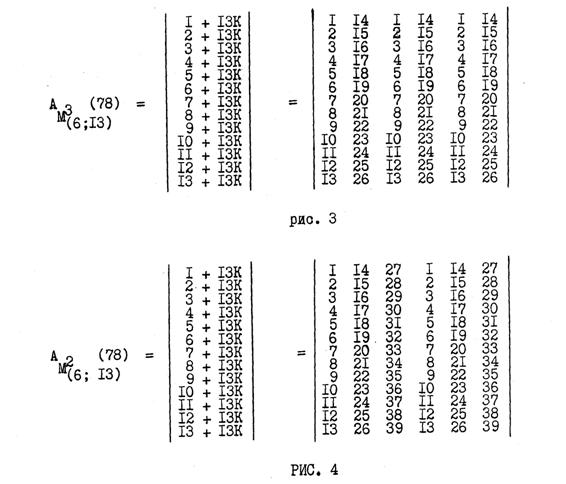
Согласно формуле (1), пс.экв−ые варианты вышеприведённых числовых матриц для конечного множества А(36) при с = р = 1 запишутся в следующем виде:
Полученный результат позволяет написать равенство, устанавливающее взаимосвязь между количеством пс.экв−х групп в числовых матрицах и максимальным значением числового оператора К для случая р = с = 1. Зависимость эта выражается формулой К(max) = Q - 1. Для случая, когда пс.экв−я числовая матрица содержит рефлективные группы, зависимость эта будет определяться количеством пс.экв−х групп (столбцов), входящих в одну рефлективную группу, т. е. К(max) = q - 1. Так, например, для числовой
И рассмотренного выше примера с множеством А(36) видно, что варианты четырёх видов эквивалентности пс.экв−х числовых матриц получаются из общей формулы (1) при количественном соотношении входящих в неё соответствующих элементов. Так, если Q = в , матрица будет квадратной. При Q > в , матрица прямоугольная и вытянута в горизонтальном направлении (в направлении пс.экв−х групп); при Q < в , матрица вытянута в вертикальном направлении (в направлении элементов пс.экв−х числовых групп, строк матрицы). Для горизонтальной: а = в = 1; для вертикальной а задаётся в пределах от 1 −цы до в = N. При этом К = 0 −лю.
Вариант а = в = 1 примечателен сам по себе, ибо он показывает, что натуральный ряд чисел (N) есть ни что иное, как пс.экв−я числовая последовательность, записываемая по схеме построчной пс.экв−ой числовой матрицы. Это позволяет говорить, что натуральный ряд целых чисел − построчно псевдо − эквивалентен.
Оба варианта построчных матриц (горизонтальный и вертикальный) содержат одно и то же количество пс.экв−х числовых элементов и располагаются на плоскости по отношению друг друга под углом 90 градусов. Такая взаимная ориентация качественно отражается на самих матицах. При "горизонтальном" варианте, конечное множество N состоит из Q групп по одному числовому элементу в каждой. При этом количество групп Q и мощность n конечного множества N по величине совпадают, т. е. Q = n и матрица является пс.экв&minusой по отношению групп. При вертикальном расположении конечного множества N матрица содержит только одну группу. Количество строк (Λ) в матрице равно мощности n конечного множества N и такая матрица будет уже построчно рефлективной, ибо каждый элемент матрицы построчно эквивалентен самому себе, следовательно, и группа будет рефлективной.
Таким образом, поворот числовой матрицы в плоскости на 90 градусов, приводит к качественному её перерождению: она, по отношению составляющих её числовых элементов из построчно пс.экв−ой превращается в рефлективную и наоборот, из рефлективной в построчно пс.экв−ую. Однако произведение Q • Λ в обоих случаях остаётся постоянным и равным мощности n конечного множества N.
Для построчно пс.экв−ой (горизонтальной) числовой матрицы, при условии в = Λ= 1, справедлива следующая формула:
n = Q • в = Q • Λ = Q/в = Q/ Λ (2)
Из этой формулы следует, что мощность n конечного числового множества N, для случая в = Λ= 1, можно получить в результате осуществления разнохарактерных операций: умножения и деления. При этом по конечному результату оба эти выражения и Q • Λ; Q/ Λ, и Q • в ; Q/в будут эквивалентны (рефлективны). По характеру же выполняемых в них операций − псевдо эквивалентны, ибо умножение не эквивалентно делению. Однако, в этом случае для нас важно то обстоятельство, что мощность n конечного множества N можно записать в виде рациональной дроби, для которой величина Q • Λили Q • в , т. е. произведение числителя на знаменатель есть ни что иное, как высота рациональной дроби по операции умножения.
Если же мы это правило распространим и на все остальные пс.экв−ые числовые матрицы, которые слагают пс.экв−ую мощность Рn конечного множества N, то получим ряд эквивалентных (антиподно эквивалентных) рациональных дробей, у которых произведение числителя на знаменатель − высота эквивалентной рациональной дроби, есть величина постоянная. В то же время следует заметить, что условие постоянства произведения Q • Λ= n или Q • Λ= N − условие эквивалентности, одновременно предопределяет две формы записи эквивалентных рациональных дробей: Q/ Λи Λ/Q. Это различие одновременно отражает и различие в конфигурации самих пс.экв−х числовых матриц, ибо, как было показано выше, поворот матрицы на плоскости на 90 градусов ведёт к взаимной трансформации величин Q и Λдруг в друга. При этом эквивалентная рациональная дробь Q/ Λ, при Q > Λраспространяется на пс.экв−ые числовые матрицы, которые вытянуты в горизонтальном направлении − в направлении групп (столбцов), а эквивалентная рациональная дробь Λ/Q на те пс.экв−ые числовые матрицы, для которых Q < Λ, т. е. вытянутых в вертикальном направлении − направлении числовых элементов, строк матрицы. В случае Q = Λ − матрица квадратная.
Так, например, в конечном числовом множестве А(36), на эквивалентную рациональную дробь Λ/Q приходятся дроби 1/36; 2/18; 3/12; 4/9 , а на дробь Q/ Λ, соответственно, 9/4; 12/3; 18/2; 36/1. Для случая Q = Λ, дробь 6/6.
Располагая эти дроби в соответствующем порядке друг за другом, мы получим структурный, Эквивалентный Математический Ряд рациональных дробей (сокращённо ЭМРN) для конечного числового множества А(36), отражающего его пс.экв−ую мощность Рn:
1/36; 2/18; 3/12; 4/9; 6/6; 9/4; 12/3; 18/2; 36/1
В отношении этого ряда эквивалентных и одновременно антиподно эквивалентных дробей необходимо отметить, что общее количество дробей определяется из условия кратности своим сомножителям и их комбинациям. Однако в натуральном ряде целых чисел N есть те, которые не имеют сомножителей − это простые числа. Они делятся только сами на себя и на единицу. Поэтому для конечных числовых множеств N, содержащих интервал чисел от 1 −цы до какого−либо простого числа включительно, присущи только две числовые матрицы: одна построчно пс.экв−ая (горизонтальная), другая, псевдо рефлективная (вертикальная). Для таких множеств ЭМРN будет иметь вид, как показано ниже на примере множеств А(7) и А(13):
1/7; 7/1 1/13; 13/1
Продолжая разговор об ЭМРN для конечных числовых множеств из натурального ряда целых чисел, следует отметить присущую им однотипность формы записи рациональной дроби в крайних позициях. В крайней левой располагается дробь вида 1/ Λ, а в крайней правой Q/1. Эти две формы записи конечных множеств из натурального ряда целых чисел представляют два вида числовых матриц: Q/1 − построчно пс.экв−ая (горизонтальная), а 1/ Λ− построчно рефлективная (вертикальная). По отношению друг друга эти матрицы располагаются на плоскости под углом 90 градусов. Наличие такой взаимной ориентации позволяет получить одну матрицу из другой, производя поворот одной из них на 90 градусов относительно заданной точки поворота. Воспользуемся этим свойством получения одной матрицы из другой и осуществим поворот, например, горизонтальной пс.экв−ой числовой матрицы относительно т. 0 против часовой стрелки на 360 градусов. В итоге получим результат, который представлен на рис. 5. матрицы
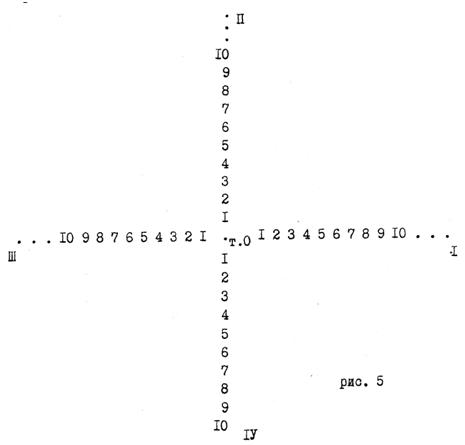
Из этого рисунка видно, что при повороте горизонтальной пс.экв−ой числовой матицы относительно т. 0 на 360 градусов, были получены следующие числовые матрицы:
Положение 1: горизонтальная пс.экв−ая числовая матрица (исходная позиция).
Положение 2: вертикальная псевдо рефлективная числовая матрица.
Положение 3: зеркальная горизонтальная, пс.экв−ая числовая матрица.
Положение 4: зеркальная вертикальная псевдо рефлективная числовая матрица.
Если же теперь, каждому числовому интервалу от одной числовой позиции до другой, мы поставим в эквивалентное соответствие равные отрезки прямой и, в добавок, зеркальные числовые матрицы запишем со знаком минус (−), то в результате такого совмещения на плоскости получим две, взаимно перпендикулярные числовые оси, представляющие собой прямоугольную систему координат. По горизонтальному направлению осей откладываются порядковые номера пс.экв−х групп, а по вертикальному, порядковые номера строк матриц.
Исходя из полученного результата, по отношению натурального ряда целых чисел, можно сделать вывод, что в основе применяемого на практике метода прямоугольных координат заложен метод манипулирования с числовыми матрицами: двух построчно пс.экв−х (горизонтальных) и двух псевдо рефлективных (вертикальных).
Полученный результат позволяет производить графическое построение числовых матриц в прямоугольной системе координат. В результате числовая матрица будет изображаться в виде прямоугольника со сторонами Q и Λ. Площадь такого прямоугольника будет равна произведению Q • Λи в своей основе будет определять, с одной стороны, мощность соответствующего конечного множества N , а с другой, высоту эквивалентной (аниподно − эквивалентной) рациональной дроби Q/ Λили Λ/Q. ∗)
____________ ∗)примечание: рациональная эквивалентная дробь, по внутренней структуре одновременно является и антиподно − эквивалентной рациональной дробью, ибо числитель, по месту положения в дроби, является антиподом знаменателю; числитель располагается над дробной чертой, а знаменатель под ней.
____________
В тоже время, если мы воспользуемся общепринятыми в Математике обозначениями горизонтальной и вертикальной числовых осей для прямоугольной системы координат, то нам следует обозначение пс.экв−х групп Q заменить на Х, а обозначение количества строк Λ, на У и тогда, всё последующее изложение материала вести применительно к этим обозначениям. В результате появляется возможность в отношении пс.экв−х числовых матриц использовать те же правила, которые применяются для точек, изображаемых в прямоугольной системе координат. При этом с точкой мы будем отождествлять не только её координаты, но и одновременно и соответствующую этим координатам числовую матрицу.
Так, например, у точки М(5; 7) координата Х = 5, а У = 7. Этой точке можно поставить в соответствие пс.экв−ую числовую матрицу, у которой количество пс.экв−х групп равно 5 −ти, а количество строк (или же алгоритм построения матрицы в , ибо в = У) равно 7 −ми. Этой матрице, при условии р = с = 1, соответствует формула:
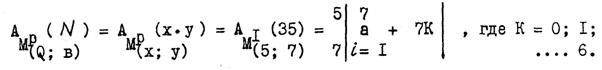
В приведённом примере знаки при Х и У положительны и, поэтому, данная числовая матрица в плоской прямоугольной системе координат будет располагаться в 1 −ой четверти.
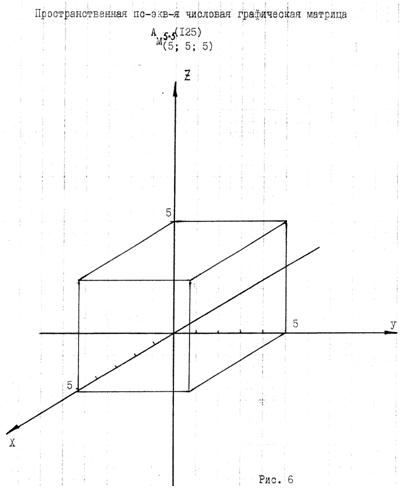
Приведённые выше сведения касались пс.экв−х числовых матриц, которые располагаются в плоскости и поворот одной из них осуществляется около т. 0 относительно оси, проходящей через эту точку перпендикулярно самой плоскости (см. рис. 5). Однако подобный поворот можно осуществить также и относительно оси, располагающейся непосредственно в плоскости рисунка, т. е. относительно прямой с позициями 2 − 3 ( или же оси У). В результате такого дополнительного поворота пс.экв−ой числовой матрицы из положения 1, против часовой стрелки на 360 градусов в плоскости, перпендикулярной плоскости рис. 5, мы получим уже пространственную систему прямоугольных координат, состоящую из четырёх построчных (горизонтальных) пс.экв−х числовых матриц и двух псевдо рефлективных (вертикальных). Для наглядности, ниже приводится пример построения пространственной пс.экв−ой числовой матрицы для конечного множества А(125), у которой Х = У = Z = 5. Эта матрица, запишется в следующем виде:
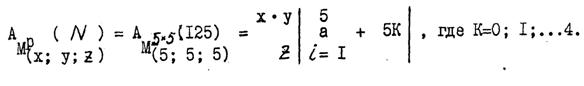
Полученный результат, как и в случае с плоскими пс.экв−ми числовыми матрицами, позволяет производить графическое построение матриц, которым присуща пространственная форма в виде прямоугольного параллелепипеда или куба. В зависимости от занимаемого октанта, матрица будет иметь следующую структуру эквивалентной рациональной дроби:
В соответствии с этим ЭМР, соответствующий структурный ряд конечного множества А(125) для каждого из этих трёх вариантов будет иметь следующий вид:
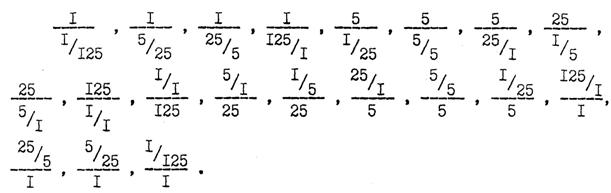
В прямоугольной системе координат, изображённой на рисунке 6, как и в случае с плоской
Исходя из вышеизложенного, мы можем констатировать, что и в случае плоской, как и в случае пространственной систем координат, соответствующий поворот матрицы на 90 градусов ведёт одновременно к оборачиваемости эквивалентно взаимосвязанных величин по функциональной предназначенности.
Примечательным фактом, в деле графической интерпретации числовых матриц, является то обстоятельство, что каждой числовой матрице можно поставить в эквивалентное соответствие точку, у которой координатами являются, соответственно, количество пс.экв−х групп и псевдо рефлективных строк, которым в эквивалентное соответствие можно поставить также и отрезки прямой определённой длины. Этим самым появляется возможность и на отрезки прямой распространить понятие эквивалентности и пс.экв−ти и их, так же как и числа, объединять в соответствующие группы (принцип Единства и Подобия!).
В то же время, из Математики известно, что поведение точки на координатной плоскости или в пространственной системе координат можно описывать уравнением различной степени. В свою же очередь, решение последнего сводится к отысканию точки, координаты которой, будучи подставлены в уравнение, обращают последнее в тождество. Это обстоятельство позволяет сделать вывод, что итоговым действием при решении какого−либо уравнения является отыскание координат точки и соответствующей пс.экв−ой числовой (графической) матрицы. Одновременно с этим определяются и параметры эквивалентной рациональной дроби.
Другими словами, нам требуется доказать, что решение уравнения, описывающего поведение точки в вышеназванных системах координат, можно представить в виде эквивалентных (пс.экв−х) множеств посредством корней уравнения. Если мы докажем это утверждение хотя бы, например, для уравнения Хˆ 2 + РХ − С = 0, то в последующем нам не составит труда перейти к уравнениям с другими степенями, Однако, в нашем случае это не самоцель, а лишь стремление выявить такую возможность.
Итак, переходя к доказательству данного утверждения, которое мы проведём на примере разбора календарной проблемы, предварительно дадим очень краткую характеристику состояния этой проблемы на данный момент времени.
2. Рефлективно − числовые матрицы, как математическая основа построения
постоянно действующих во времени календарей.
При построении систем мер обычно применяется принцип простых кратных соотношений между устанавливаемыми единицами. Для мер времени этот принцип осуществляется только при установлении мелких единиц: секунды, минуты и часов. Более крупные же единицы: сутки, неделя, месяц и год, возникли на основе астрономических явлений, и соотношения между ними лишены такой простоты.
Как известно, время суточного оборота Земли не кратно времени её годового оборота вокруг Солнца. Астрономический год составляет приблизительно 365,242195 суток, т. е. 365 суток 5 часов 48 минут 46 секунд, а время одного оборота Луны вокруг Земли не кратно времени ни суточного, ни годового оборота Земли (астрономический месяц составляет приблизительно 29,530588 суток, т.е. 29 суток 12 часов 44 минуты 3 секунды). Необходимость устанавливать крупные единицы времени простыми кратными соотношениями, приводила к различным неувязкам и погрешностям в календаре на всех этапах его становления и развития, от глубоко древности до наших дней.
В древнем солнечном календаре, который использовался в своё время в Египте, из−за несоответствия точному астрономическому соотношению (все годы считались по 365 суток) система сутки − год была несовершенной. Этот показатель был "блуждающим": даты перемещались относительно астрономических точек и сезонов года ∗) приблизительно на сутки (на 23 часа 15 минут 4 секунды) каждые четыре года, а за столетие − приблизительно на 24 дня.
______________ ∗) Астрономическими точками или моментами, определяющими времена года, т. е. сезоны, считаются в настоящее время день весеннего равноденствия (20 или 21 марта), летнего солнцестояния (21 или 22 июня), осеннего равноденствия (22 или 23 сентября) и зимнего солнцестояния (21 или 22 декабря).
______________
Для установления недостатка в 46 г. до н. э. Юлий Цезарь включил в каждое четырёхлетие один дополнительный високосный день (юлианский календарь), а с 1582 г. в Советской России перешли на ещё более точный григорианский календарь, в котором каждые 400 лет исключаются три високосных дня в годах конца столетий, первые две цифры которых не делятся на 4. Поэтому 1700, 1800 и 1900 гг. не были по григорианскому календарю високосными, а 2000 г. должен быть високосным. В результате устранён источник погрешности, возникавший из−за сложного соотношения между сутками и астрономическим годом. Расхождение в одни сутки образуется только за 3323 года, что не имеет практического значения.
Система же неделя месяц − год, т. е. внутренняя структура календаря (примечание авт.: данная структура представляет собой соответствующую числовую матрицу), остаётся несовершенной до настоящего времени. Главный недостаток действующего календаря в том, что числа месяцев каждый год переходят с одних дней недели на другие. Это причиняет много неудобств. Выходные дни всех недель ежегодно меняют свои числа, праздничные − перемещаются по дням недели. Причина этого недостатка − один "лишний" день в году (в високосном − два), нарушающий отношение простой кратности между неделей и годом (365 = 7 • 52 + 1). Другой недостаток − различное число дней в месяцах и кварталах года. Третий недостаток заключается в отсутствии простой кратности в соотношении недель с месяцами, в раздроблении недель между месяцами, кварталами и годами. Это нарушает стройность календарной системы и затрудняет увязку недельного планирования с месяцами, кварталами и годовым.
Перечисленные выше недостатки, которые в одинаковой мере были присущи различным ранее и ныне действующим календарям: лунным, лунно − солнечным и солнечным, вызывали необходимость их совершенствования. При этом процесс совершенствования, носил двойственную направленность. С одной стороны совершенствовалась внешняя структура, т. е. правило високосов − ,сутки − год, с другой, внутренняя, т. е. система неделя − месяц − год. Проведённые реформы были подчинены астрономическим параметрам ввиду необходимости изменить календарь так, чтобы он соответствовал фактическому соотношению астрономических суток и года. Этот процесс завершился с принятием григорианской реформы в 1582 г., в результате которой календарный год практически совпадает с астрономическим. И сейчас, по общему мнению, григорианская система високосных годов является гибкой и достаточно точной, и пересмотра не требует.
В то же время, последние два столетия отмечены стремлением усовершенствовать внутреннюю структуру календаря. Промышленный переворот в Европе в конце 18 века, индустриализация 19 века и научно − техническая революция 20 века делают всё более актуальной эту проблему. Актуальность данной проблемы стала настолько очевидной, что необходимость введения постоянного календаря не могут игнорировать и современные религиозные общины. Так, руководители католической церкви на Втором ватиканском соборе, состоявшемся в 1964 − 64 г., высказались в пользу постоянного календаря, что зафиксировано в решении собора. Следовательно, одно из существенных препятствий в деле реформы календаря в глобальном аспекте отпадает. В то же время, это решение предусматривает минимальные изменения, которые не затрагивают вопроса сокращения семидневной недели. По этому вопросу все церкви в настоящее время будут возражать.
В 1953 году по инициативе правительства Индии вопрос о реформе календаря был поставлен в Организации Объединённых Наций. Необходимость эта была вызвана тем, что на территории страны, вплоть до настоящего времени, используется около ста календарей, отличающихся друг от друга датой начала года, числом месяцев, а также названиями месяцев. Экономический и Социальный совет ООН в 1954 г. одобрил проект постоянного календаря. При этом, в качестве предлагаемых вариантов, были два: французского философа Огюста Контома (1849 г.) и календарь французского астронома Гюстава Армелина (1888 г.). Структура первого содержала 13 месяцев по 28 дней и одного дня в году, не имеющего названия (1 + 13 • 28 = 365). Он вставлялся после субботы последнего, 13 −го месяца, перед Новым годом, как дополнительный день отдыха. В високосном году такой же день отдыха вставлялся также после субботы 6 −го месяца. Однако 13 −ти месячный календарь имел бы ряд существенных недостатков хотя бы потому, что при делении года на кварталы пришлось бы делить и месяцы.
По этой причине главное внимание уделялось второму варианту. По нему календарный год состоит из 12 месяцев и делится на 4 квартала по 91 дню в каждом (1 + 4 • 91 = 365). Первый месяц квартала имеет 31 день, два остальных по 30. Первое число года и квартала приходится на воскресенье, а каждый квартал заканчивается субботой и имеет 13 недель. В каждом месяце 26 рабочих дней. В простом году один день, как международный праздник мира и дружбы народов, вставляется после 30 декабря, в високосном году праздничный день високосного года вставляется ещё после 30 июня (табл. 1).

Помимо вышеприведённых вариантов календарей, в настоящее время предлагается пять проектов, которые имели бы действительное реальное значение и являлись бы оптимальными, каждый в своём роде. По степени изменений действующего календаря эти проекты можно отнести к трём уровням: минимального изменения, умеренных изменений и радикальных изменений. В проекте минимум, вариант Володомонова В.Н., день 31 −го декабря исключается из недельного (но не месячного) счёта. Календарь становится постоянным, а при фиксировании начала недели в понедельник нет раздробления недель между кварталами и годами. Структура того календаря представляется в виде 1 + 1 • 28 + 5 • 30 + 6 • 31 = 365. То есть один день, как и в предыдущих двух, выносится за пределы структурной сетки (матрицы), строящейся по принципу простых кратных соотношений, а кварталы представлены: один 92 днями (3 −тий квартал) и три 91 днём. В високосном году день 29 февраля не входит в недельный счёт: 28 февраля постоянно должно быть средой, а 1 марта − четвергом (см. табл. 2):
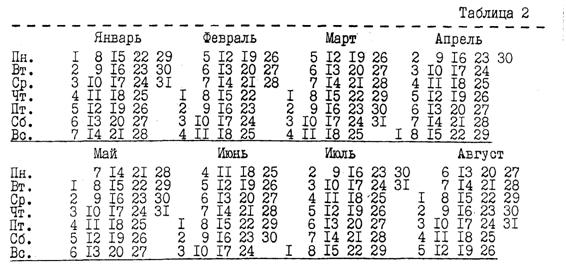
При сравнении вышеприведённых трёх вариантов календарей видно, что отличительным признаком постоянства их внутренней структуры является непременное условие: вынос одного дня из 365 за пределы недельного счёта. Сами же недельные (внутренние) структуры могут быть разнообразными и существенно отличаться друг от друга. Это же свойство − вынос одного дня за пределы недельного счёта, сохранено и в одном из предлагаемых умеренных вариантов. Его структура представляется в виде 1 + 8 • 30 + 4 • 31 = 365 (см. табл. 3).
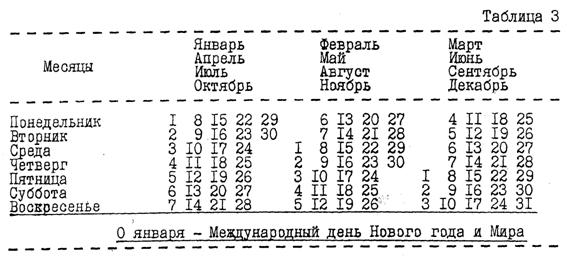
В другом варианте умеренного календаря оптимальность достигается за счёт выравнивания числа дней в месяцах по признаку минимального перемещения дней в месяцах. Февраль дополняется до 30 дней за счёт января и марта. В результате семь месяцев будут иметь по 30 дней, а пять − май, июль, август, октябрь и декабрь, по 31. Структура такого календаря представляется в виде 7 • 30 + 5 • 31 = 365. Если такой проект рассматривать как дальнейшее (после проекта минимум или календаря Володомонова В.Н.; см. табл. 2) усовершенствование календаря, то пятым месяцем, сохранившим 31 день, окажется не декабрь, а январь.
Наконец два радикальных проекта предусматривают изменение продолжительности недели и переход на шесть пятидневных недель в месяце с целью устранения весьма существенного недостатка календаря − раздробление недель между месяцами. В каждый из этих проектов вписывается как изменения по проекту минимум, так и распределение дополнительных дней в конце кварталов. Високосный день в умеренных и радикальных проектах следует фиксировать 31 февраля по принципу минимального перемещения дат. Во всех пяти проектах исключаются из недельного счёта день стабилизации календаря и високосный день, а в радикальных проектах ещё и четыре дня в конце кварталов.
Если учесть все разнообразные материалы, то получается не одна сотня "проектов". Но дело не в учёте и накоплении проектов, а в выявлении наиболее оптимального варианта на основе математического анализа физики самого явления − процесса перемещения системы Земля − Луна в пространстве вокруг Солнца.
2.1. Анализ внутренней структуры календаря.
Проводя анализ внутренней структуры календаря на предмет её постоянства во времени, обратим в первую очередь внимание на то, что в своей основе отражает календарь. Известно, что календарь − это система отсчёта времени, которая отражает сложный процесс вращения системы Земля − Луна в течение одного годового оборота вокруг Солнца.
Воспользуемся одним из правил Теоретической механики, согласно которого сложное движение можно представить как сумму простых движений. Представим этот процесс в следующем виде:
если, например, Земля, подобно Луне, будет при движении по орбите вокруг Солнца повёрнута к последнему всё время одной и той же стороной (сделаем такое предположение), то совершив один годовой оборот вокруг Солнца, она сделает в пространстве вокруг своей мнимой оси один оборот. Вычтем этот один оборот из (365 + С) оборотов, которые система Земля − Луна совершает за один год. Здесь С − часть неполного оборота, учитываемая в високосном году. Затем из оставшихся оборотов вычтем 13, которые приходятся на вращение самой системы Земля − Луна в году ∗).
_______________ ∗) Солнечный год содержит дробное число лунных месяцев (приблизительно 12,4). Чтобы включить в солнечный год лунные месяцы без их дробления, прибавили целый лунный месяц раз в несколько лет, приближая эти лунные годы к солнечным годам. Такие удлинённые годы содержали, следовательно, по 13 лунных месяцев. В этом и заключается основная идея лунно − солнечного календаря, который явился, таким образом, комбинацией лунных месяцев с солнечными годами. Этим же правилом воспользуемся и при проведении анализа внутренней структуры календаря.
_______________
Тогда на саму Землю придётся (364 + Ч) − 13 = (361 + С) оборотов. Опустим пока величину С − високос из наших рассуждений. Обоснованность этого будет показана ниже. После этого, общее количество оборотов за год системы Земля − Луна равное 365 можно представить в следующем виде:
1 + 13 + 351 = 365.
Произведём ряд преобразований в этом выражении, представив число 351 в виде: 351 = 13 • 27 = = 13 • (1 + 13 + 13). После подстановки и последующего преобразования получим:
1 + 13 + 351 = 1 + 13 + 13(1 + 13 + 13) = 1 + 13 + 13ˆ 2 + 13ˆ 2 = 1 + 2 • 13(1 + 13) = 1 + 14 • 26.
В результате вышеизложенной методики и соответствующих численных преобразований получилась новая, внутренняя структура календаря 1 + 14 • 26. Эта структура, с одной стороны, отличается от предыдущих тем, что содержит или 14 месяцев по 26 дней, или наоборот, 26 месяцев по 14 дней (примечание: соотнесение чисел 14 и 26 с наименованиями месяц − число дней и наоборот, с математической точки зрения равноправно по отношению обоих сомножителей и это свойство чисел выступать одновременно в различных качествах будем именовать свойством м а т е м а т и ч е с к о г о д у а л и з м а), а с другой, она подобна им, ибо также имеет вынесенный один день за пределы календарной сетки, сетки недельного счёта ∗).
_______________ ∗) Выше приведённая методика расчёта внутренней структуры календаря была выполнена с СССР в 1978 г. Её автором является т. Акинфиев В.И.
_______________
А теперь обратим наше внимание на промежуточный результат преобразования и выпишем его отдельно: 1 + 13 + 351 = 1 + 13 + 13(1 + 13 + 13) = 1 + 13 + 13 + 13ˆ 2 + 13ˆ 2 = 1 + 2 • 13 + 2 • 13ˆ 2 = 365.
В данном случае, конечный промежуточный результат представляет полное квадратное уравнение не приведённого вида, структурно отражающего процесс вращения системы Земля − Луна по оборотам на орбите вокруг Солнца. Следовательно, его можно записать в общем виде, положив Х = 13:
2Хˆ 2 + 2Х + 1 + 365. (3)
С учётом високосного остатка это уравнение можно переписать в более полном виде:
2Хˆ 2 + 2Х + 1 + С = 365 + С.
Так как С − это часть неполного оборота (високос), приходящегося на каждый год, находится в левой и правой частях равенства, то при дальнейшем анализе его из уравнения можно удалить. После этого решим полученное уравнение, предварительно произведя в нём соответствующие преобразования: 2Хˆ 2 + 2Х + 1 = 365; 2Хˆ 2 + 2Х − 364 = 0; Хˆ 2 + Х − 182 = 0.
В буквенном выражении уравнение запишется в следующем общем виде: АХˆ 2 + ВХ − С = 0.
Для нашего случая А = В = 1. После подстановки находим корни уравнения: Х(1; 2) = {− В ± √ B ˆ2− 4AC)} /2 = { − 1 ±( √1+4•1•182)}/2 = (− 1 ± 27) /2.
Корни этого уравнения: Х(1) = 13; Х(2) = − 14.
А теперь постарается выяснить, за что "отвечают" оба эти корня. Для этого при дальнейшем анализе отнесём 13 оборотов системы Земля − Луна только к Земле, т. к. с точки зрения календаря они являются равноправными по отношению остальных оборотов и, следовательно, влиянием Луны можно, с позиции календаря, пренебречь.
Выпишем снова уравнение (3). Подставим в него сначала Х(1) = 13, а затем Х(2) = − 14 и произведём соответствующие преобразования:
1 + 2Х + 2Хˆ 2 = 1 + 2 • 13 + 2 • 13ˆ 2 = 1 + 26 + 13 • 26 = 1 + 26(1 + 13) = 1 + 14 • 26 = 365.
1 + 2Х + 2Хˆ 2 = 1 + 2 • (−14) + 2 • (−14)ˆ 2 = 1 + 2(−14){1 + (−14)} =
1 + 2(−14)(−13) = 1 + 2 • 14 • 13 = 1 + 14 • 26 = 365.
Сравнивая оба конечных результата, можно сделать вывод, что при числовой интерпретации конечного результата знак минус перед вторым корнем, с точки зрения чисто арифметического преобразования, никакого принципиального значения не имеет (примечание: при геометрической интерпретации конечного результата решения данного и подобного, приведённому квадратному уравнению, знак минус перед вторым корнем имеет вполне определённое физическое значение. Он указывает направление на плоскости или в пространстве соответствующей величины или параметра, ориентируемого по отношению прямоугольной или пространственной системы координат) и в обоих случаях получается одна и та же внутренняя структура календаря (см. табл. 4):

Соотнесём полученный результат в виде матричной структуры 1 = 14 • 26, с внутренней структурой ныне действующего календаря. Для этого спроецируем его на календарную матрицу 1 = 14 • 26. В результате получится матрица, содержащая в себе обе структуры календарей и 1 + 14 • 26, и 28 + 4 • 30 + 7 • 31 , где числа 28; 30 31 представляют количество дней в соответствующих месяцах григорианского календаря; см. рис. 6а. Рис. 6а.

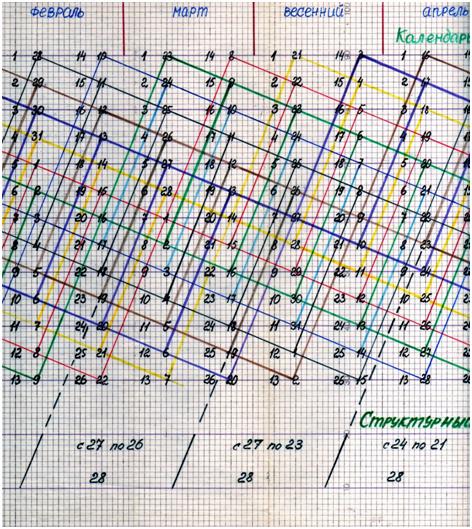
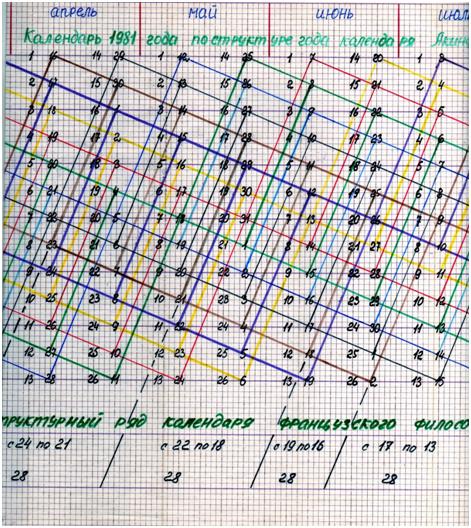
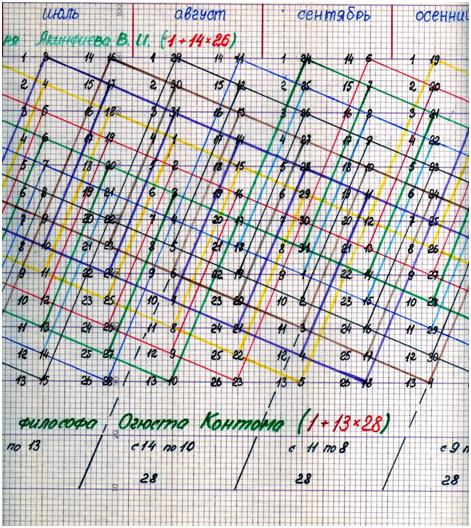


Анализ графической прорисовки (рис. 6а) позволяет выявить следующее: если мы будем следовать вдоль наклонной линии четвергов календаря 1981 года: см. наклонную линию чёрного цвета, исходящую от 1 −го января, то на каждый двойной промежуток, следующий друг за другом ( см. промежутки: 1 − 15 − 29; 29 − 12 − 26; 26 − 12 − 26; 26 − 9 − 23; 23 − 7 − 21; 21 − 4 − 18; 18 − 2 − поднимаемся вверх до 16 июля; затем снова движемся по наклонной вниз 16 − 30 − 13; 13 − 27 − 10 и т. д. до 31 декабря), приходится одинаковое количество дней, но уже в вертикальных столбцах, равное 28. При этом каждый следующий месяц начинается с числа на наклонной прямой пятниц. В случае января имеем 29 дней, т. к. количество дней в этом месяце равно 1 + 28.
Сведение полученного графического результата к структурной записи посредством чисел, позволяет сделать вывод, что мы получили внутреннюю структуру 1 + 13 • 28, т. е. календарь французского философа Огюста Контома (1849 г.). Таким образом, анализ графической прорисовки (рис. 6а) позволяет сделать вывод, что разные по форме внутренние структуры трёх календарей по содержанию отражают одно и то же уравнение 2Хˆ 2 + 2Х + 1 = 365. Естественно возникает вопрос: "Почему это так и сколько таких обособленных структур содержится в данном уравнении?"
При ответе на поставленный вопрос обратимся вновь к результату преобразований уравнения (3), когда в него подставляются значения корней Х(1) =13 и Х(2) = − 14. Конечный результат решения обоих уравнений был дан в виде структурной записи 1 + 14 • 26. То есть число 2 объединялось с числом 13. Однако, с таким же успехом мы можем произвести объединение чисел 2 и 14. В результате получится внутренняя структура 1 + 13 • 28. Эта структура по своей сути отражает внутреннюю структуру календаря, который был предложен в позапрошлом веке О.Контоном (1849 г.), и ещё ранее М.Мастрофини (1834 г.). Наличие этого факта позволяет констатировать одинаковость результатов, как по линии графической прорисовки, так и по линии чисто численного решения.
Если мы теперь воспользуемся этим свойством, объединения различных сомножителей в числе 364, то получим целую номенклатуру внутренних структур постоянно действующих календарей. Число 364 имеет следующие сомножители: 1; 2; 2; 7 и 13. Учитывая обстоятельство, что числа, представляющие внутреннюю структуру календаря, могут выступать в двух качествах: месяца или дня, т. е. обладать свойством математического дуализма, мы можем после выполнения различных комбинационных сочетаний простых сомножителей между собой, а также и самими комбинациями, для числа 364 получить ряд внутренних структур постоянно действующих календарей:
1 + 364; 1 + 2 • 182; 1 + 4 • 91; 1 + 7 • 52; 1 + 13 • 28; 1 + 14 • 26; 1 + 26 • 14; 1 + 28 • 13; 1 + 52 • 7; 1 + 91 • 4; 1 + 182 • 2; 1 + 364 • 1.
Каждой из этих внутренних структур, постоянно действующих на определённом временном интервале календарей, соответствует определенная форма записи уравнения, являющегося разновидностью общего уравнения (3); см. табл. 6.

После этого, с учётом данных таблицы 6, можно сделать следующие выводы:
1. Внутренняя, структурная форма (числовая матрица) того или иного постоянно действующего календаря, представленная в данном случае числом 365 = 1 + 364, получается из данной структуры, являющейся основной, посредством различных комбинаций простых чисел, являющихся сомножителями большего слагаемого − числа 364. При этом использование любой из них в качестве постоянно действующего на соответствующем временном интервале календаря, ни в коей мере не изменяет общепризнанного правила високосов григорианского календаря.
2. Приведённый выше ряд внутренних структур постоянно действующих календарей построен в строгом соответствии с принципом простых кратных соотношений между устанавливаемыми единицами: м е с я ц − д е н ь. Согласно, этого правила, кратность достигается посредством выноса ("выброса") за пределы матричной структуры сетки определённого количества единиц. В данном случае 1 −цы.
3. С позиции Математики, внутренние структуры календарей, обладающие свойством постоянства во времени, представляют собой эквивалентные, псевдо эквивалентные числовые множества. С помощью их число (конечное множество) 364 (примечание: а в общем случае любое конечное числовое множество N из натурального ряда целых чисел (N)) может быть представлено в эквивалентной или псевдо − эквивалентной записи группа − количество элементов в группе, посредством соответствующих рефлективных числовых матриц.
4. Различные по внутренней структуре календари, обладающие свойством временного постоянства, по содержанию отражают одно и то же уравнение: 1 + 2Х + 2Хˆ 2 = 365 или АХˆ 2 + ВХ − С = 0.
Выводы, полученные в результате сравнительного, очень простого математического анализа, показывают, что постоянство календаря во времени, лишь в том только случае возможно, если его внутренняя структура строится в строгом соответствии с теорией множеств, а именно, с теорией числовых эквивалентных множеств. А для этих множеств, одним из характерных свойств является свойство компактной (наиболее оптимальной) записи (представления) числа (соответствующего конечного множества), когда количество эквивалентных (псевдо эквивалентных) групп равно количеству элементов в эквивалентной (псевдо эквивалентной) группе. Наличие этого обстоятельства, позволяет выявить в эквивалентном (антиподно − эквивалентном) ряде внутренних структур постоянно действующих календарей, наиболее оптимальную, которая может быть основной. С этой целью проанализируем структуры постоянно действующих календарей, предварительно записав их в соответствии с псевдо − эквивалентной мощностью Р(N) = 364 в виде структурного, эквивалентного математического ряда рациональны дробей (ЭМРN) для числа 364:
1/364; 2/182; 4/91; 7/524 13/28; 14/26; 26/14; 28/13; 52/7; 91/4; 182/2; 364/1.
Для выявления наиболее оптимальной эквивалентной структуры данного ЭМРN, воспользуемся наглядным сравнением площадей прямоугольников, у которых стороны представляют числитель и знаменатель эквивалентных, рациональных дробей (см. рис. 7):
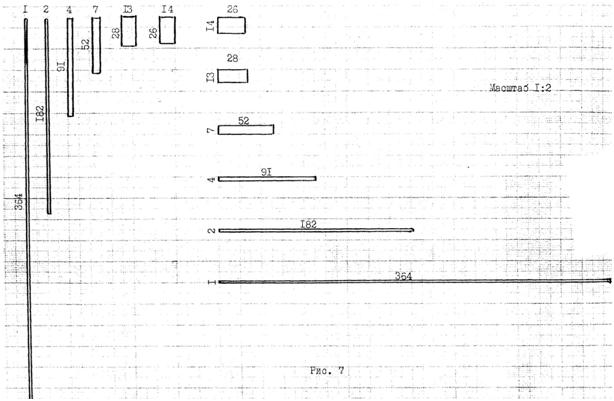
Из сравнения площадей прямоугольников водно, что наиболее близкими к "квадрату", т. е. к "квадратной" эквивалентности, являются структуры дробей 14/26 и 26/14 (в таблице 6 варианты 6 и 7). Первая эквивалентная дробь соответствует матричной структуре 1 + 14 • 26 (вариант календаря Акинфиева В.И.), вторая, "перевёрнутому" варианту календаря Акинфиева В.И., т. е. структуре 1 + 26 • 14. Одновременно с этим, чтобы определить, какая из структур вариантов 6 и 7 наиболее предпочтительна (оптимальна), необходимо учесть факт исторического развития человеческого общества − количество месяцев в ныне действующем, григорианском календаре (12 месяцев в году). Учёт этого фактора по отношению эквивалентных структур вариантов 6 и 7, из которых первая выполнена по уравнению 1 + 2Х + 2Хˆ 2 = 365, а вторая по уравнению 1 + 2Х(1 + Х) = 365, позволяет сделать вывод, что наиболее близкой к григорианскому календарю является структура варианта 6. И хотя структура варианта 7, т. е. 1 + 26 • 14, и сохраняет традиционную 7 −ми дневную структуру недели, существенным её недостатком, с точки зрения истории развития человеческого общества, является наличие 26 месяцев в году по 14 дней в каждом (см. таблицу 7):
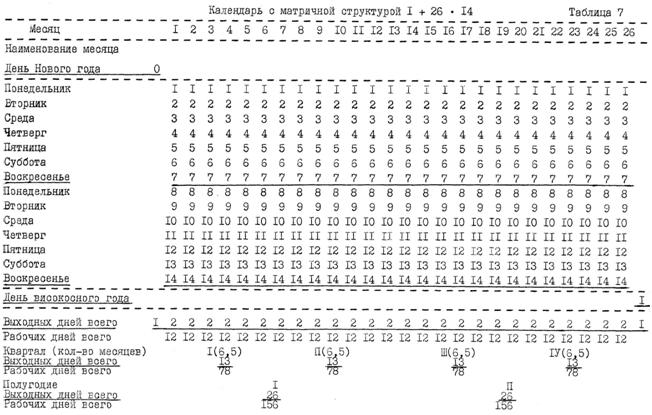
К особенности варианта 6: необходимо отнести следующие при фактора ∗):
1. Чередование выходных дней по схеме 2 − 1 − 2 − 1 и т. д.
2. Наличие шестидневной недели.
3. Наличие в кварталах не целого количества месяцев, а 3,5.
В отношении остальных вариантов структур ЭМР364 (примечание: расшифровывается как структурный, эквивалентный математический ряд рациональных дробей числа 364) можно сказать, что они менее предпочтительны, т. к. в одном случае имеет место наличие большого количества дней в месяцах и малое количество самих месяцев, а в другом, наоборот.
Исходя из вышеизложенного по анализу внутренних структур календарей на предмет оптимальности и постоянства во времени, с позиции эквивалентных (антиподно − эквивалентных) числовых множеств, можно сделать вывод, что наиболее предпочтительной на современном этапе эволюции Земли, на период сохранения Землёй современной скорости вращения, является внутренняя структура 1 + 14 • 26 (календарь Акинфиева В.И.).
_________________
∗)Следует отметить принципиальную разницу внутренних структур календарей варианта 6 в табл. 6 и в табл. 4. Как было показано в первой части статьи "Краткие сведения об эквивалентных и антиподно − эквивалентных числовых множествах", одной из структурных характеристик псевдо − эквивалентных числовых матриц является величина q − общее количество псевдо − эквивалентных групп − столбцов в одной рефлективной группе. Она определяет конструктивное построение числовых, псевдо − рефлективных числовых матриц. Так, при q = 1 , количество псевдо − эквивалентных групп в одной рефлективной группе равно 1 и число рефлективных групп, соответственно, равно общему количеству столбцов в матрице. При этом максимальное количество элементов, составляющих одну рефлективную группу, численно равно алгоритму в её построения. Так, для варианта 6 в табл. 6, общее количество рефлективных групп, в псевдо − эквивалентной матрице, равно 14 и алгоритм её построения в = 26. В отличие от этой матицы, матрица табл. 4 выполнена с показателем q = 2. Алгоритм её построения в = 13. В соответствии с этими характеристиками, общее количество столбцов увеличивается до 28 и матрица в конструктивном плане вытягивается в горизонтальном направлении. Для обеих числовых матриц, что в табл. 6, и табл. 4, матричные формулы соответственно будут иметь следующий вид:
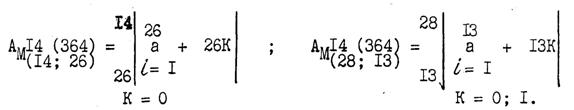
_________________
2.2. Анализ внешней структуры календаря.
Структурный ряд ныне действующего календаря можно записать в следующем виде:
31; 28; 31; 30; 31; 30; 31; 31; 30; 31; 30; 31 или в общем виде: Х + 4Х(1) + 7Х(2) = 365, где Х = 28; Х(1) = 30; Х(2) = 31.
Исторически сложилось так, что хотели люди этого или нет, но в ряду с эквивалентной структурой 1 + 4 • 91 или 1; 30; 30; 31; 30; 30; 31; 30; 30; 31; 30; 30; 31 (примечание: этому структурному ряду соответствует календарь французского астронома Гюстава Армелина; 1888г.) произвели внутриструктурные перестановки: ликвидировали один "свободный" день и из февраля убрали ещё два. Это привело к тому, что ныне действующий календарь нельзя использовать на каждый год. Периодичность повторения его внутренней структуры как следует из практики, составляет 28 лет.
Этот, 28 −ми летний промежуток, подобно внутренней структуре календаря, также имеет соответствующую структуру построения, именуемой внешней структурой календаря, и связана она с правилами високосов. По этому правилу, через каждые четыре года, к внутренней структуре календаря добавляется один оборот (сутки), который компенсирует неучтённые примерно 0,25 ежегодных, дополнительных земных оборотов за предыдущий трех летний промежуток времени. Это правило учёта високосов в григорианском календаре признано мировым сообществом наиболее оптимальным и не требует изменений.
Однако оно не является единственным вариантом учёта високосов. С целью выявления их общего количества и наиболее оптимального из них, воспользуемся вышеприведённой методикой и для 28 −ми летнего временного промежутка, т. е. конечного числового множества А(28), распишем соответствующий ЭМР28, отражающий псевдо − эквивалентную мощность Р(n)28. Одновременно с этим, ниже, против каждой эквивалентной рациональной дроби, запишем дополнительное количество оборотов, приходящихся на один високосный цикл. В результате получим следующие два структурных ряда:

Из структурного ряда а) следует, что наиболее оптимальными для структуры високосных циклов, в 28 −ми летнем интервале повторяемости календаря, являются два псевдо − эквивалентных варианта, близких к структуре "квадрата" − "квадратной" эквивалентности. Это варианты 4/7 и 7/4. Первый состоит из 4 −х високосных циклов по 7 лет в каждом, а второй, из 7 −ми високосных циклов по 4 года в каждом. В то же время, между этими вариантами имеется существенная разница, определяемая числом дополнительных суток (високосных оборотов) в одном високосном цикле. Для первого это 1,75 оборота, а для второго, один целый оборот. С точки зрения эквивалентных множеств и практики пользования целочисленными оборотами при учёте високосов григорианского календаря, наиболее оптимальным является вариант эквивалентной структуры рациональной дроби 7/4. Исходя из этого, можно констатировать, что в историческом прошлом составители григорианского календаря как раз и "вышли" на структуру високосов 7/4. Однако следует отметить, что это решение, несомненно, носило чисто интуитивный характер.
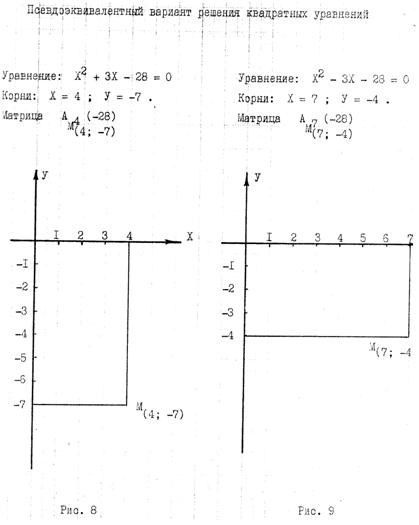
А теперь, т. к. числитель и знаменатель данной эквивалентной дроби являются корнями соответствующего квадратного уравнения, в соответствии с формулами Виета можно записать само уравнение, регламентирующее правило високосов для данного эквивалентного варианта. Так, В = Х + У = 7 + (−4) = 3; q = Х • У = 7 • (− 4) = − 28 (примечание: в данном случае q в квадратном уравнении приведённого вида обозначает свободный член уравнения С ). В соответствии с этими величинами, уравнение будет иметь следующий вид: Хˆ 2 − 3Х − 28 = 0.
Если бы оптимальным вариантом был бы вариант 4/7, то для него Х = 4, а У = − 7. Тогда В = Х + У = 4 + (− 7) = − 3 и q = Х • У = 4 • (− 7) = − 28. Этому варианту соответствует уравнение вида: Хˆ 2 + 3Х − 28 = 0 (примечание: этим уравнением, описывается и структура всем известной игры в домино: в игре задействованы 28 фишек и количество играющих 4 −ре человека; каждый получает в начале по 7 фишек и участники располагаются попарно под углом 90 градусов друг к дугу).
Сравнивая обе формы квадратных уравнений для двух псевдо э− эквивалентных вариантов, можно констатировать, что при переходе от одной эквивалентной рациональной дроби, к другой через дробь со структурой "квадрата", знак при коэффициенте В, в соответствующем квадратном уравнении у неизвестного в первой степени меняется на противоположный.
Для календаря Акинфиева В.И. (1 + 14 • 26), регламентирующим фактором построения структуры одного високосного цикла, так же как и в случае григорианского календаря, должен быть один дополнительный оборот (одни сутки) в течение одного високосного цикла. Это регламентирующее требование предопределяет равенство корня У, определяющего количество лет в одном високосном цикле, 4 −ём. Исходя из этого, второй корень Х − количество високосных циклов, в рассматриваемом промежутке времени, будет равно 1, т. к. за основу мы берём один 4 −х летний промежуток и целостность добавочного високоса. Следовательно, эквивалентная рациональная дробь будет иметь вид 1/4 , а структура ЭМРN, соответственно, 1/4; 2/2; 4/1. Соответственно этому ряду, эквивалентных рациональных дробей, ряд високосов представится в виде: 1; 0,5; 0,25.
Исходя из приведённых выше соображений, принимаем Х = 1 и У = − 4. Тогда В = Х + У = 1 + (− 4) = − 3 и С = Х • У = 1 • (− 4) = − 4. В соответствии с этими значениями, уравнение будет иметь вид: Хˆ 2 + 3Х − 4 = 0.
А теперь подведём итог по вышеизложенному.
После того, как выявлены наиболее оптимальные эквивалентные структуры рациональных дробей из ЭМРN, определяющих внутреннюю и внешнюю структуру календарных, псевдо − эквивалентных числовых матриц, можно сформулировать и правила построения постоянно действующих структур календарей во времени:
1. Постоянно действующий календарь должен состоять из месяцев, построение которых должно быть в строгом соответствии с теорией эквивалентных (антиподно − эквивалентных) числовых множеств. При этом оптимальность структуры как внешней, так и внутренней, задаётся соответствующей эквивалентной (антиподно − эквивалентной) рациональной дробью из ЭМР28 и ЭМР364 (примечание: при наличии современного количества земных оборотов за год; для другого количества, из ЭМРN необходимо использовать другое число).
2. Недостающее количество суток до общего количества суток в году (365), располагается отдельно, вне основной, рефлективной, числовой календарной матрицы. Этот недостающий день или дни, есть Фликкер выброс (примечание: о Фликкер выбросе смотри статью "Электромагнетизм" в журнале "Самиздат", автор Лавров М.А.).
3. Нельзя производить перестановки дней из одного месяца в другой, т. е. из одной рефлективной группы в другую, ибо этим нарушается эквивалентное соответствие между рефлективными группами (месяцами) и одновременно на практике ведёт к непостоянству внутренней структуры календаря во времени.
Итак, после того как на примере календарной проблемы, доказано утверждение, что решение уравнения, описывающего поведение точки в прямоугольных координатах, можно представить в виде эквивалентных (псевдо − эквивалентных) числовых множеств посредством корней уравнения вида АХˆ 2 ± ВХ − С = 0, можно сделать следующие обобщённые математические выводы:
1. Корни приведённого полного квадратного уравнения Хˆ 2 ± РХ − С = 0 "устанавливают" связь между структурной формой самого уравнения и соответствующей структурой эквивалентных (псевдо − эквивалентных) числовых множеств, эквивалентных (псевдо − эквивалентных) числовых матриц, структурно представляющих свободный член уравнения С и находящихся с ним в кратных отношениях. Или: уравнение вида Хˆ 2 ± РХ − С = 0 можно структурно представить в виде эквивалентных числовых множеств (эквивалентных или псевдо − эквивалентных рефлективных числовых матриц) посредством его корней.
2. Уравнение вида Хˆ 2 ± РХ − С = 0, посредством своих корней регламентирует наиболее оптимальный (компактный) вариант эквивалентной (псевдо − эквивалентной) числовой матрицы, по структуре наиболее близкой к "квадратной" эквивалентности, из соответствующего ЭМРN.
3. Так как любому конечному множеству А(N) из натурального ряда целых чисел, присуще своя псевдо − эквивалентная мощность Р(n) (примечание: не путать Р(n) c коэффициентом при Х в уравнении Хˆ 2 ± РХ − С = 0), то из этого следует:
3.1. Каждому конечному числовому множеству А(N), из натурального ряда целых чисел (N), присуща единственная форма полного квадратного уравнения приведённого вида, регламентирующая его псевдо − эквивалентную мощность Р(n) по наиболее оптимальному варианту построения псевдо − эквивалентных числовых матриц.
3.2.Так как для любого, конечного числового множества А(N) из натурального ряда целых чисел, в соответствии с формулой:
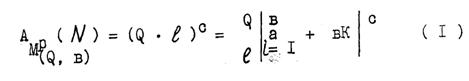
3. Структурно − функциональный анализ квадратного уравнения вида:
Хˆ 2 ± РХ − С = 0
После того, как на примере решения квадратной проблемы, доказана взаимосвязь между эквивалентными (псевдо э− эквивалентными: − далее везде пс.экв−ми) числовыми множествами и полным приведённым квадратным уравнением вида Хˆ 2 ± РХ − С = 0 ∗), следует остановиться на ряде вопросов по отношению уравнений данного типа. К числу таковых отнесём следующие:
1. Какую функциональную роль "выполняют" с позиции эквивалентных, а также пс.экв−х числовых множеств (числовых матриц) коэффициент Р при неизвестном Х в первой степени?
2. Чем обусловлено различие (сочетание) буквенного обозначения корней вышеприведённого уравнения в статье по схеме Х и У, и общепринятого обозначения в Математике Х(1) и Х(2) или У(1) и У(2) и т. д.?
3.Чем регламентируется использование знаков + и − перед коэффициентов Р при неизвестном Х в первой степени и перед свободным членом уравнения С?
______________ ∗) Вопрос о наличии такой связи, по отношению всех видов числовых множеств в Математике, в данной статье не рассматривается.
______________
Чтобы ответить на эти вопросы, рассмотрим операции сложения и вычитания ∗∗) пс.экв−х числовых матриц. Данные операции разберём на примере вышеприведённых уравнений Хˆ 2 + 3Х − 28 = 0 и Хˆ 2 − 3Х − 28 = 0. Одновременно с этим, в целях наглядности выполняемых операций, соответствующие этим уравнениям пс.экв−е числовые матрицы изобразим в плоской системе прямоугольных координат (о наличии такой возможности было показано выше), ставя в эквивалентное соответствие пс.экв−ой группе соответствующий длины отрезок числовой оси Х, а строке, отрезок числовой оси У. Непременным условием при этом будет равенство подобных отрезков по обоим направлениям. После этого, непосредственно перейдя к самим уравнениям, найдём их кори и соответствующие им пс.экв−е числовые матрицы изобразим графически в прямоугольной системе координат.
______________ ∗∗) В целях сокращения объёма статьи, операции умножения, деления, возведение в степень, извлечение корня, логарифмирование, дифференцирование, интегрирование и т. д. пс.экв−х числовых матриц, не рассматриваются, хотя сами по себе эти операции, в отношении этих матриц, представляют определенный интерес.
______________
Согласно, общепринятой методики построения точки в прямоугольной системе координат и, естественно, соответствующую этой точке графическую пс.экв−ю числовую матрицу, можно строить, исходя из наличия корней уравнения, определяемых по формулам Виета. При этом само построение можно осуществлять двумя способами:
1. Значения корней непосредственно откладываются по соответствующим направлениям числовых осей. В результате сразу получается пс.экв−я числовая матрица, в виде соответствующего прямоугольника. Это наиболее короткий путь построения. По этой методике построены пс.экв−е числовые матрицы
![]()
![]()
______________