В данной статье излагается математический подход к решению одной из древних загадок, дошедших к нам из глубокой древности − проблемы пирамидальных сооружений далёкого прошлого, таких как пирамида Хеопса, Хафра (Хефрена), Менкаура, Храма IV, оставшегося от цивилизации Майя в Гватемале, и ряда других.
Исследователи многих стран пытались ответить на вопросы: "Что является исходной причиной возведения не только этих, но и других колоссов представителями разных цивилизаций, существовавших на Земле в разное историческое время? Диктуется ли подобная необходимость только лишь погребальными соображениями?" Необходимого ответа на данные вопросы пока что нет.
В статье автор иcходит из версии, что строительство пирамид грандиозных размеров, в первую очередь обусловлено соображениями информационного характера. Пирамида − это долговременная информационная система, позволяющая "передавать" не только математическую, но и другую информацию через большие промежутки времени. В качестве доказательства этой версии, в статье использован математический подход − решение данной проблемы на базе эквивалентных (антиподно − эквивалентных) числовых множеств. С целью облегчения прочтения статьи, в ней даются не только математические основы пирамидальных сооружений далёкого прошлого, но и необходимые сведения из Математики, позволяющие неподготовленному читателю без особых затруднений читать данную статью.
Содержание статьи:
1. Числовая, эквивалентная пирамида (ЧЭП).
2. Биноминальная числовая пирамида (БЧП).
3. Заключение.
Одной из отличительных особенностей, присущих одновременно этим тайнам, является наличие у них географического признака. И если вера в "загадочность" простого числа 13 имеет широкий географический ареал распространения, то пирамидальные сооружения расположены по планете не так повсеместно: в Египте, ряде стран Азиатского региона и Американского континента. При этом все эти сооружения, несмотря на разнообразие своего географического положения, характеризуются одним общим для них признаком: временем своего существования. Они являются своеобразными "долгожителями" нашей планеты.
Сам факт существования подобных сооружений, с одной стороны, нас удивляет; с другой − восхищает, а с третьей − приводит в недоумение: так всё же, что послужило первопричиной их возведения в далёком прошлом? Не уж − то только культовые соображения, которые были связаны с захоронением усопших?
Подобных вопросов имеется немало, а вот ответов, ни одного. Взять хотя бы последние сенсационные (прим.: данная часть статьи была написана в период 1983 ÷ 1988 гг., поэтому эти открытия следует относить, возможно, к тому периоду времени) открытия французских и японских учёных по раскрытию тайн пирамиды Хуфу (Хеопса − греч.). Как не велики их заслуги в этом деле, однако главной своей тайны, объясняющей причину её возведения в прошлом, пирамида так и не "раскрыла". Да к тому же, в отношении этой пирамиды до сих пор вообще много неясного. С одной стороны, она вроде бы была предназначена для погребения останков фараона, а с другой, несмотря на их тщательные поиски, они до сих пор не обнаружены. Наличие такого объективного факта заставило, ряд исследователей, усомниться в её предназначенности как погребального сооружения и была выдвинута гипотеза о наличии закодированных знаний в элементах её конструкции.
Подобное утверждение само по себе не беспочвенно и в этом отношении следует указать на исследования бывшего сотрудника института проблем надёжности и долговечности машин АН Белоруссии Сергея Борисовича Проскурякова (см. газету "Неделя" Љ34 за 1987 г.). По Проскурякову выходит, что в элементах конструкции пирамиды Хеопса закодирована разнообразная научная информация. В соотношениях её конструктивных элементов, можно выявить информацию об основных закономерностях астрономии и математики, зашифрованное суммарное изложение таблицы мер и весов, сведения из высшей математики: они манипулировали, например, понятием "число пи в степени пи". Интересен сам факт использования проектировщиками пирамиды метрической системы исчисления, появившуюся во Франции . . . . в конце 18 века! Есть информация и о физических понятиях. Так, например, сумма периметра основания и высоты пирамиды составила (с абсолютной точностью) одну миллиардную долю расстояния, которое проходит свет в вакууме за час! Имеется и другая, не менее интересная информация.
Конечно, наличие подобной информации в элементах конструкции пирамиды само по себе интересно. Однако она не проливает свет на истоки самой идеи пирамидальной и, притом, ступенчатой конструкции сооружения. И поэтому, хотя работа Проскурякова С.Б. и заслуживает внимания, но отсутствие в ней объяснений по поводу возникновения самой идеи строительства именно ступенчатой пирамиды, заставляет подходить к его работе весьма осторожно, т. к. в его действиях можно усмотреть элемент преднамеренности: "втиснуть" имеющиеся знания современной науки в элементы конструкции пирамиды.
В противоположность исследователям, видящим в деяниях древних зодчих разумное начало, имеются и другие, которые придерживаются теории "глупых строителей". Согласно этой теории, "древние мол, сами не ведали, что творили", а результат их творения: чистая случайность (см. статью "Послание из глубины веков" авт. А.Смирнова, в газете "Московский комсомолец" за 4 декабря 1987 года).
Эта полемика вокруг пирамиды Хеопса оставляет в тени другие подобные сооружения. А их, как следует из объективной действительности, на нашей планете не так уж и мало, да и форма их исполнения не везде одинакова. Взять хотя бы, ту же пирамиду Хеопса; так называемый, храм IV, оставшийся от цивилизации Майя на севере Гватемалы, в районе Петен; пирамиды Солнца; Луны в древнем городе Теночитлане на севере − востоке Мексики − см., например, журнал НЛО Љ19 (684) за сентябрь 2011г.). Или же пагоды в странах Азии. Все эти сооружения разнообразны по форме, и в то же время, все они пирамидальные сооружения.
Наличие такого очевидного факта приводит к постановке следующих вопросов:
1.Случайно ли то, что пирамидальные сооружения прошлого представлены достаточно широким географическим ареалом?
2. Только ли случайностью объясняется желание древних зодчих, в разных концах планеты, возводить разные по форме пирамидальные сооружения?
3. Случайно ли разнообразие в формах конструкций пирамидальных сооружений, а если нет, то где следует искать истоки этой случайной разнообразности?
Конечно, проще всего в творении древних зодчих видеть элемент случайности. Но в наш век − век научного прогресса, вряд ли кого удовлетворит такой подход к проблеме пирамидальных сооружений. Поэтому напрашивается вывод: не лучше ли "встать" на другую позицию и признать за древними зодчими наличие у них знаний, которых, несмотря на наши впечатляющие достижения, у нас пока ещё нет. Ведь в противном случае мы давно уже разгадали бы не только тайны древних сооружений, но и замыслы самих зодчих.
Наличие двух противоположных точек зрения на проблему пирамидальных сооружений показывает, что к решению этой проблемы можно подходить по разному. А, исходя из этого, и применять различные методики исследований. Однако какими бы они не были, все их можно классифицировать с двух позиций: позиции следствия и позиции причины.
Позиция следствия предопределяет сам факт "существования" пирамидальных сооружений и их изучение на базе имеющихся достижений в различных областях науки, как−то математики, геологии, археологии и т. д. Однако, как показывает подобная практика, результаты этих исследований сравнительно "скромны". С их помощью пока не получен ответ на вопрос: зачем понадобилось древним зодчим, в разных частях планеты строить, требующие больших материальных и людских затрат, столь громоздкие сооружения?
Так, например, высота пирамиды Хеопса 147 м.; Хафра (Хефрена), соответственно, 143 м.; Менкаура (Микерина) 66 м. Храма IV , оставшегося от цивилизации Майя в Гватемале 50 м. А в Индии, например, среди пагод имеются две уникальные: одна расположена на берегу моря и имеет высоту 101 м.; уникальность другой, тоже достаточно высокой (42 м.), обусловлена её конструкцией. Выполнена она в виде пустотелых, уменьшающихся в направление к вершине, металлических кубов (прим.: в самые первые дни 1987 года, по центральному телевидению, в передаче "Клуб путешественников", был показан видовой фильм о пагодах Китая и Индии, в котором, наряду с другими, были показаны и вышеупомянутые).
В противоположность позиции следствия, позиция причины предопределяет факт осознанной необходимости строительства долговременных пирамидальных сооружений грандиозных размеров. И вот тут − то сразу и возникает вполне очевидный вопрос: "А на каком этапе развития цивилизации возникает эта осознанная необходимость и из чего исходят её истоки?"
Конечно, сейчас, по истечении не одного тысячелетия, очень трудно ответить на эти вопросы утвердительно и мы можем только догадываться о причинах, повлекших за собой строительство пирамид и других подобных сооружений. Однако, нас никто не ограничивает в праве выдвинуть соответствующую гипотезу на этот счёт и в её подтверждение привести соответствующие доводы. Естественно возникает вопрос: "А с каких позиций лучше всего это сделать?" Представляется, что лучше всего с позиции Математики.
Очевидность такого подхода, можно объяснить тем, что строительство любого сооружения предопределяет осознанное соблюдение определённых математических соотношений и закономерностей между элементами строительной конструкции. По характеру же последних, с одной стороны, без предвзятого мнения можно судить об уровне математических и, связанных с математикой, других знаний древних зодчих; с другой, соответствующим образом классифицировать целесообразность их деятельности, а в третьих, появляется возможность соотнести уровень наших знаний с их уровнем развития.
Для того, чтобы это сделать, необходимо располагать соответствующей математической методикой (или набором математических критериев), позволяющей осмысленно, с позиции Математики, подойти к комплексной оценке деятельности древних зодчих. О том, как это можно сделать, и повествуется в этой статье.
В заключении хочется сказать о том, что этой статьёй автор не претендует на окончательное решение проблемы пирамидальных сооружений прошлого. Им лишь сделана попытка, с позиции эквивалентных множеств, хотя бы в первом приближении, приблизиться к комплексному пониманию сути самой проблемы. А о том, насколько это удалось, − судить уже читателю.
ЧИСЛОВАЯ ЭКВИВАЛЕНТНАЯ ПИРАИДА (ЧЭП).
Обратимся к Математике и посмотрим на неё вот под каким ракурсом: предположим, что перед нами поставлена задача: передать в далёкое Будущее информацию (послание) о предмете Математика и понятиях, содержащихся в ней. При этом, конечно, предполагается очень высокий уровень её развития.
В связи с постановкой такой проблемы возникает вопрос: "В какой форме целесообразнее всего это сделать и что следует передавать в Будущее?" Ведь получивший в будущем такое послание человек (а именно ему адресуется это послание), во − первых, понял бы, что речь идёт о предмете Математика, а во − вторых, смог бы из почерпнутых сведений составить представление о её содержании. Но вот тут, со стороны читателя может возникнуть вопрос: "А зачем нам нужно решать эту, да при том ещё очень сложную проблему, изобилующую многими неизвестными?"
Да, неизвестных в этой проблеме очень много! Однако, главным в этом многообразии неизвестных являемся мы . . . люди, наша цивилизация, ибо непонятна та роль, которую эта проблема "отводит" нам самим со всеми имеющимися у нас на сегодняшний момент времени достижениями в науке. Или мы (цивилизация) выступаем в роли передающей цивилизации, или же принимающей? Если выявится, что нам в этом вопросе отведена вторая или пусть даже промежуточная роль, то сразу встаёт вопрос: "Где и что следует нам искать, и от кого соответствующая информация должна была исходить для нас в далёком Прошлом?"
Исходя из сказанного, перед нами вырисовываются две первоочередные задачи:
1. Выявление формы передачи информации.
2. Определение места передачи.
Чтобы ответить на эти и ряд других вопросов, которые могут возникнуть при решении поставленной выше проблемы, нам, в первую очередь, следует (хотя бы в первом приближении) выявить минимальный объём сведений, которые из всего математического многообразия подлежит передачи в Будущее. Естественно, что при этом нам следует руководствоваться критерием разумности и минимальной достаточности.
Итак, первые представления об объектах Математики у представителей рода человеческого возникли ещё в глубокой древности и были связаны с потребностью количественно характеризовать окружающие его предметы, а также предметы человеческого труда. Потребность в счёте привела к открытию чисел 1, 2, 3, 4 и т. д., из которых в последующем был составлен натуральный ряд целых чисел 1, 2, 3, 4, 5, 6, 7, . . . . ∞ (N), где ∞ − символ бесконечности. В современном представлении этот числовой ряд представляет монотонно возрастающую числовую последовательность от 1−цы до бесконечности, являющуюся одновременно Арифметической прогрессией с разностью d = 1.
Применение этой числовой последовательности, на практике ограничивается каким−либо конечным числом (множеством), в результате чего она становится конечной. Примером одной из таких, числовых последовательностей является, например, последовательность от 1 −цы до 365−ти. Эту числовую последовательность можно записать тремя способами: горизонтально, вертикально и по формуле
В случае, когда N является квадратом целого числа Х, его алгебраическое выражение можно представить в виде N = Хˆ2. Если же число N не подпадает под это условие, то его можно представить в виде двух слагаемых, одно из которых являет собой "квадратную" форму эквивалентной записи ближайшего к числу N числа по недостатку, другое − остаток (слагаемое), который будучи сложенным с Хˆ2, даст число N. Этот числовой остаток представляет собой числовой "Фликкер выброс", который возникает в случае выделения из целого числа N ближайшего к нему числа, имеющего структуру "квадратной" эквивалентности. В результате для любого числа N из натурального ряда чисел мы получим алгебраическое выражение, позволяющее записывать любое число по форме "квадратной" эквивалентности: а + Хˆ2 = N.
Изложенная выше методика получения структуры "квадрата" может быть перенесена на все остальные числа (конечные числовые множества) натурального ряда чисел. В результате этот числовой ряд, записываемый по схеме "квадратной" эквивалентности, предстанет перед нами в следующем виде: см. таблицу 9.

1. Натуральный ряд целых чисел (N), записанный по схеме "квадратной" эквивалентности − схема "квадрата", разбивается на числовые промежутки (интервалы), в которых базой "квадратной" эквивалентности выступает число, одновременно определяющее и номер числового интервала.
2. При последовательном переходе от одного эквивалентного числового интервала к другому, количество числовых позиций увеличивается на две.
3. Количество числовых позиций в любом числовом эквивалентном интервал характеризуется нечётным числом.
А теперь, воспользуемся чистым листом бумаги и проведём на нём вертикальную ось. После этого, учитывая схему построчно горизонтальной записи каждого эквивалентного числового интервала, расположим их последовательно друг под другом так, чтобы они расположились симметрично относительно вертикальной оси (см. табл. 10).

Следовательно, можно сделать вывод:
натуральному ряду целых чисел (N), записываемому по схеме "квадрата" − квадратной эквивалентности, в качестве наиболее компактной записи присуща форма плоской ступенчатой пирамиды. Обозначим её тремя буквами: ЧЭП − плоская, числовая эквивалентная пирамида.
Анализируя эту форму компактной записи, отметим присущие ей закономерности построения:
1. Любое натуральное целое число в эквивалентной, числовой ступеньке пирамиды, можно "получить" в результате прибавления к числам предыдущей эквивалентной числовой ступеньки , соответствующей "высотной характеристики" или числа, характеризующего числовой интервал или числовой промежуток между предыдущей и последующей эквивалентными числовыми ступенями ЧЭП. Так, например, для получения чисел второй эквивалентной, числовой ступеньки, достаточно к числам первой прибавить поочерёдно число 4; для получения третьей ступеньки, к числам второй прибавить число 6 и т. д.
Если же теперь подобные высотные, числовые характеристики, объединим с понятием высоты соответствующих эквивалентных числовых ступенек ЧЭП, то сможем записать, что высота первой ступеньки будет равна 4 −ём, второй 6 −ти, третьей 8 −ми и т. д.
2. При переходе от одной эквивалентной числовой ступеньки, к последующей, высота последующей каждый раз в количественном отношении увеличивается на две единицы. То есть, при движении от вершины ЧЭП к её основанию, изменение высоты её ступенек происходит по закону Арифметической прогрессии с разностью d = 2. Следовательно, высота любой ступеньки ЧЭП может быть определена по формуле общего члена данной прогрессии, т. е. а(n) =
3. Расстояние от вершины ЧЭП, до верхнего основания любой её ступеньки, равно произведению номера этой ступени на номер последующей ступени. Так, например, для 13 −ой ступеньки, расстояние от её верхнего основания до вершины ЧЭП равно: 13 • 14 = 182 ед. длины и т. д.
4. Каждая эквивалентная числовая ступенька ЧЭП, с левой стороны рисунка, начинается с квадрата числа, определяющего как номер ступеньки, так и базовое число "квадратной" эквивалентности.
При переходе в диагональном направлении, от чисел первой эквивалентной числовой ступеньки, к последующей и т. д., что справа − налево или слева − направо (смотри, например, числовую "диагональ"1 − 4 − 9 − 16 и т. д.; 2 − 5 − 10 и т. д. или 1 − 6 − 13 и т. д.; 2 − 7 − 14 и т. д.), числовые ряды, представляющие собой разность последующих и предыдущих числовых позиций (например, числовая диагональ 1 − 4 − 9 − 16 − 25 и т. д., "даст" числовой ряд 3; 5; 7; 9 и т. д.), образуются только из нечётных чисел. При этом числовой интервал при переходе от одной числовой позиции к другой, по отношению предыдущего, каждый раз возрастает в количественном отношении на две единицы. То есть, изменяется тоже по закону Арифметической прогрессии с разностью d = 2.
К этим закономерностям, которые при соответствующей интерпретации построения натурального ряда чисел (N) "предоставляет" в наше распоряжение Математика, нам следует добавить ещё условие: характер изменения расстояния между числовыми позициями в самих ступеньках ЧЭП при переходе от одной числовой ступеньки, к последующей, и тогда, выбрав соответствующий масштаб, мы сможем изобразить ЧЭП на плоскости. В основу этого дополнительного условия мы заложим требование, предопределяющее равенство высоты эквивалентной числовой ступеньки, числовому интервалу или расстоянию между тремя числовыми позициями в самой эквивалентной ступеньке.
Так, высота первой эквивалентной, числовой ступеньки равна 4 и, следовательно, общее расстояние между числовыми позициями 1 − 2 − 3 должно равняться тоже 4 −ём. В результате появляется возможность структурно "разбить" эквивалентные, числовые ступеньки на блоки, представляющие собой плоские квадраты. В соответствии с этим, первая ступень ЧЭП будет состоять из одного плоского блока; вторая, имеющая высоту в 6 единиц, из 2 −х блоков; третья из 3 −х и т. д.
В соответствии с заданной схемой построения длины эквивалентных ступенек ЧЭП, изменение длины числового интервала между двумя числовыми позициями, при переходе от одной ступеньки к последующей, будет осуществляться по закону Арифметической прогрессии с разностью d = 1. Так, если длина числового интервала между позициями 1 − 2 или 2 − 3 в первой ступени, равна 2 −м единицам длины, то во второй ступеньке, между числовыми позициями 4 − 5; 5 − 6 и т. д., будет 3 −и ед. длины; в третьей ступени 4 −ре ед. длины и т. д.
После этого, выбрав в качестве единицы длины расстояние в 1 мм, изобразим ЧЭП графически на плоскости в прямоугольной системе координат. При соблюдении вышеперечисленных условий мы получим пирамиду, которая изображена на рис. 27. На рисунке 27 масштаб М 1 : 1 указан в отношении единицы длины в один миллиметр. Сам же рисунок выполнен в масштабе 2 : 1.
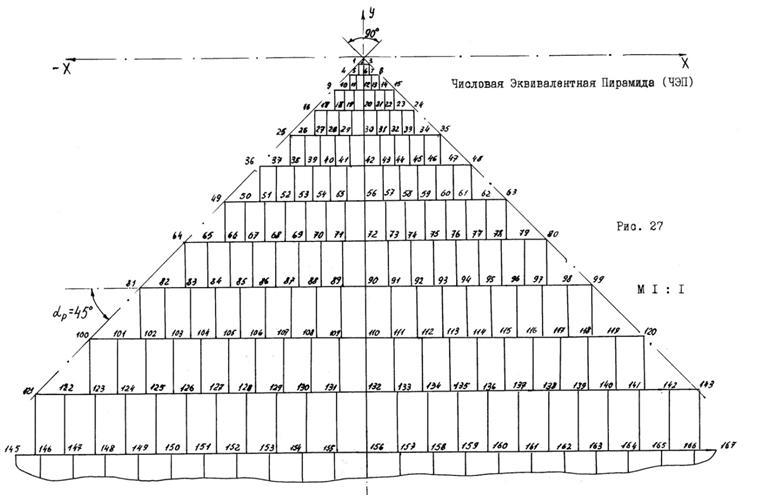
Как видно из рисунка, у такой ЧЭП угол при её вершине равен 90 градусов. Соответственно, угол при основании треугольников, включающих в себя длину ступенек ЧЭП и двух наклонных прямых, касающихся крайних числовых позиций в ступеньках (в 4 −х угольной ЧЭП данные прямые будут представлять собой апофемы), будет равен 45 градусам.
А теперь, по отношению к ЧЭП, изображённой на рис. 27, выполним ряд действий с последующим их осмыслением.
ДЕЙСТВИЕ 1.
Соединим числовые позиции числовых, эквивалентных ступенек так, как показано на рисунке 28 плавными кривыми; см. рис. 28. На рисунке 28 масштаб М 1 : 1 указан в отношении единицы длины в один миллиметр. Сам же рисунок выполнен в масштабе 2 : 1.
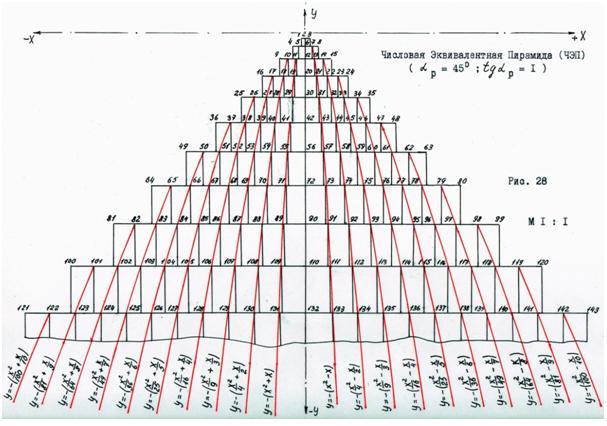
В результате этого построения, с одной стороны, каждая кривая позволит графически объединить в соответствующие числовые ряды (подмножества) числа, то есть числовые позиции, по условию пункта 1 (примечание: см. п.1 после табл. 10), а с другой, положение каждого числа в здании ЧЭП будет увязано посредством координат соответствующей числу точкой. Так, например, числовой позиции 109 (число 109), соответствует точка с координатами Х = − 11 мм; У = − 110 мм. Этим координатам удовлетворяет уравнение кривой У = − (Хˆ2 + Х).
Из произведённого выше действия1 по отношению ЧЭП следует, что в конструктивном отношении она может быть выполнена в двух вариантах. В одном случае − это ЧЭП, ступеньки которой "сложены" из плоских квадратных числовых блоков; в другом, из плоских числовых блоков, боковые поверхности которых выполнены по уравнению соответствующих кривых. В упрощённом варианте это могут быть просто наклонные прямые, соединяющие соответствующие числа, числовые позиции эквивалентных, числовых ступенек; конструкция такой ЧЭП смотри на рис. 29:

Наличие двух вариантов изображения ЧЭП, при внимательном рассмотрении позволяет выявить третий. С этой целью обратимся к уравнению вида: Х = Уˆ2 Ђ У или У = Хˆ2 Ђ Х. Эти уравнения позволяют находить координаты точек на поле ЧЭП, когда конечные числовые множества изменяются по схеме Арифметической прогрессии. Структура самой прогрессии, характеризующая изменение высоты эквивалентных, числовых ступенек ЧЭП, нам известна и, поэтому, в соответствии с формулой а(n) = а(1) + d(n − 1), определим числовые позиции для каждой числовой ступеньки в пределах рисунка 28. Определение чисел проведём на примере двух кривых (уравнений) У = Хˆ2 Ђ Х. Полученный результат запишем в виде таблиц.

По полученным значениям корней (координатам точек) построим соответствующие кривые, которые на поле ЧЭП ограничат две, симметрично расположенные области. Эти области на рисунке 30 показаны штриховкой; см. рисунок.

Эти области, при рассмотрении их с позиции пространственной формы, представляют собой плоское сечение тонкостенной конструкции, имеющую вытянутую сигарообразную форму. Эта конструктивная форма подобна вытянутой тонкостенной "оболочке". К характеристике подобной оболочке следует отнести способность соответствующим образом объединять числовые позиции (числа). Так, на наружной поверхности такой "оболочки" располагаются соответствующие числовые позиции числовых, эквивалентных ступенек, а на внутренней поверхности, проекции этих числовых позиций на основание самих ступенек.
В довершении к высказанному заметим, что нас никто не ограничивает в возможности отдельного вычленения числовых тонкостенных "оболочек" в отдельную конструкцию. В результате получится подобие пирамиды − пирамидальное сооружение. Так, например, вычленяя центральную "оболочку", мы получим пирамидальное сооружение (на плоскости), которое, в одном случае, будет представлять собой полую сигарообразную конструкцию, а в другом, сооружение из квадратных числовых блоков, стоящих друг на друге; см. рис. 31 и 32:

В отношении последней (рис. 31) следует заметить, что эта конструкция, в пространственной интерпретации, предстаёт перед нами в виде стоящих друг на друге кубов, увеличение размеров которых от вершины к основанию происходит по закону Арифметической прогрессии, с разностью d = 2 и, которые в натуре могут быть монолитными или полыми. Последний вариант, по конструктивно − технологическому признаку − пустотелым кубам, напоминает конструкцию пагоды, о которой было сказано в начале статьи "От автора". Пагода эта, находится в Индии и во временном плане является долговременным памятником, являющим собой предмет культурного наследия народов Индии, а также памятником, несомненно "несущим" в Будущее соответствующую информацию. Остаётся надеяться, что подобная информация в Будущем будет учёными "прочитана".
По отношению пирамидальной конструкции пирамиды, стоящих друг на друге кубов, отметим то обстоятельство, которое не ограничивает нас в праве несколько видоизменить данную пирамиду конструктивно. Впишем в каждый куб шар (сферу) и такую, шарообразную, пирамидальную конструкцию вычленим отдельно. Естественно ожидать, что вертикально стоять такое пирамидальное сооружение не сможет, а вот лежать − да. В результате перед нами на земле предстанет цепочка лежащих шаровых сфер, постепенно увеличивающихся в размерах. Расположить сферы можно как рядом, так и на расстоянии друг от друга.
В этой связи правомерен вопрос: "А не являются ли найденные в Коста Рике каменные сферы разных размеров (см. журнал "Тайны ХХ века" Љ48 за декабрь 2011 г.) подобным или хотя бы приближённо напоминающим вышеупомянутое сооружение; не "несёт" ли оно в Будущее соответствующую, в том числе и математическую информацию?" Такая пространственная конструкция, вполне может "содержать" информацию о ряде натуральных целых чисел, а также представление людей далёкого прошлого о наиболее компактной в эквивалентном отношении форме − форме квадрата.*)
_______________
*)Примечание: более компактным образованием на плоскости, по отношению квадрата, является окружность, а в пространстве, шарообразная сфера.
_______________
Если же мы, в довершении всего, обратимся к древнейшим философским воззрениям народов Индии, то увидим, что одним из глубоко, а вернее мистически почитаемым представлением в религии верующих, является понятие "священный квадрат", которому подчиняется весь окружающий нас Мир (в том числе и мы люди) и жизнь самой Вселенной (примечание: о возможном смысловом содержании понятия "священный квадрат", смотри статьи "Электромагнетизм" и "Структурно − функциональный анализ антиподно − эквивалентного, математического ряда ЭМРN, и ряда ЭМР(1 ÷ ∞); (− ∞ ÷ ∞) в журнале "Самиздат", авт. Лавров М.А.).
Конечно, было бы заманчиво, с научных позиций, осмыслить информацию, скрывающуюся за понятием "священный квадрат". И в то же время, для себя отметим, что в контексте статьи это понятие, именуемое просто квадратом, символизирует представление о наиболее сжатой, компактной форме какого − либо материального объекта. Таковым объектом, например, является эквивалентная, рациональная дробь, в каком − либо ряде ЭМРN. Под ней можно понимать, например, параметры того же прямоугольного параллелепипеда; соотношение (соразмерность) его сторон и т. д. На плоскости − это может быть и прямоугольник, и окружность; в пространстве прямоугольный параллелепипед и сфера и т. д. Но в любом случае, каким бы в конструктивном отношении материальный объект не был, ему, способному во временном плане изменять свою форму и т. д. по схеме развития антиподно − эквивалентного, математического ряда ЭМРN {примечание: см. статьи "Электромагнетизм" и "Структурно − функциональный анализ антиподно − эквивалентного, математического ряда ЭМРN, и ряда ЭМР(1 ÷ ∞); (− ∞ ÷ ∞) в журнале "Самиздат", авт. Лавров М.А.}, будет присуще пребывание в фазе "квадрата", т. е. наиболее сжатом, компактном состоянии.
Как обстоит дело в действительности, по отношению "священного квадрата", а именно, смысловой его трактовки с позиции наиболее сжатого, компактного состояния, которое может приобретать материальное тело (объект) в процессе своего временного развития, покажет Будущее, а пока что отметим проблематичность данного предположения и вернёмся к пирамидальным сооружениям (примечание: для сведения читателей: работа "Математика, Календарь, Пирамиды", была написана автором, в самом начале работы над темой "Теория Квадрата" и смысловое содержание "квадрата" было понято уже потом).
Говоря о различии конструктивного исполнения ЧЭП, для пирамид, изображённых на рисунках 27 ÷ 30. отметим единство идеи их построения. Это обстоятельство позволяет ввести для них общую характеристику, определяющую их равновеликость или эквивалентность. В качестве одной из таковых (обозначим её через
В общем же случае, α(р) может быть любым углом в пределах: 0 <α(р) <90 градусов. Поэтому правомерен вопрос: "А как отразится изменение угла α(р) на конструкции ЧЭП?"
Ответ будет зависеть от того, какой из конструктивных параметров ЧЭП, определяющий её эквивалентность, мы примем в качестве постоянного. Если постоянной будет длина ступенек ЧЭП, то с изменением α(р) будет меняться высота ступенек. При стремлении α(р) к 90 градусам, высота ступенек будет расти, в противном случае убывать. Если постоянной будет высота эквивалентных, числовых ступенек, то при стремлении α(р) к 90 градусам, длина ступенек будет убывать, в противном случае возрастать.
Таким образом, перед нами вырисовываются два равноправных варианта ЧЭП с различными углами пирамидальности:
Вариант 1 − постоянство длины ступенек и переменность их высоты.
Вариант 2 − постоянство высоты ступенек и переменность их длины.
Из сказанного следует, что угол пирамидальности α(р) может изменяться в пределах от значений близких к 0, до значений, близких к 90 градусам. Однако в любом случае, каким бы он ни был, длина эквивалентных ступенек (по Вар.1) или их высота (по Вар. 2) , остаются неизменными. Этим самым подчёркивается принадлежность любой пирамиды к ЧЭП. Для наглядности сказанного, на рисунке 33 даётся изображение ЧЭП с К(р) = 1,2738 и α (р) = 51 градус 52 минуты.

Примечание: В 1981 году, в одной из передач "Клуба путешественников", посвящённой проблеме пирамидальных сооружений далёкого прошлого, был показан киноматериал о пирамиде Хеопса. Так вот, когда оператор с кинокамерой перемещался по внутренним переходам пирамиды, им была показана часть плоской стены, на которой схематично были изображены прямоугольные, плоские блоки, очень похожие на плоские, числовые блоки ЧЭП рисунка 33. Сразу же возник вопрос об их предназначении. Но ни в момент показа фильма, ни сейчас, ответа на него нет. Остаётся надеяться на получение ответа в Будущем, а пока что это примечание можно отнести к разряду "Информация к размышлению".
Данной ЧЭП, среди себе подобных, присуще замечательное конструктивное качество: частное от деления удвоенной длины любой из её ступенек на расстояние от самой ступеньки до вершины, есть величина постоянная и равна трансцендентному числу π , с точностью до четвёртого знака после запятой (3.1416).
_______________
*) Примечание: надо отдать ложное знаниям древних строителей пирамиды Хеопса; именно эти значения К(р) и α(р) были ими задействованы при строительстве данной пирамиды.
_______________
Подобным образом, с точностью до четвёртого знака, можно закодировать в ЧЭП трансцендентное число е = 2,7182, применяемое в Математике в качестве основания натуральных логарифмов. У ЧЭП с константной е, К(р) = 1,4715 и α(р) = 55 градус 48 минут. Подобное конструктивное качество для каждой ЧЭП, произвольно взятой в пределах 0 <α(р) <90 градусов, будет иметь тоже свойство постоянства. Поэтому его тоже можно использовать в качестве "постоянной" ЧЭП.

Выявив возможности конструктивного "встраивания" в здание ЧЭП двух замечательных констант Математики, предпримем попытку совмещения обоих констант в здании одной ЧЭП. Для этого поступим следующим образом: конструктивное "встраивание" числа π в здание ЧЭП мы оставим без изменения. Соответственно, К(р) и α(р) у такой ЧЭП будут: 1,2738 и 51 градус 52 минуты. А по отношению числа е выдвинем условие: характеризовать ЧЭП по высотному признаку, а точнее, по количеству в ЧЭП эквивалентных, числовых ступенек. Эта возможность обусловливается наличием известной формулы
Полагая в этой формуле равенство параметра с номеру эквивалентной ступеньки ЧЭП и, переписывая саму формулу в виде {(с + 1)/с}ˆс, мы найдём, что для "встраивания" числа е (образно, в высоту ЧЭП) с точностью, например, до второго знака после запятой, достаточно выполнить условие, чтобы у ЧЭП было 338 ступенек. В соответствии с этим количеством ступенек, число е будет равно:
Если ограничиться данной точностью числа е, то сможем констатировать, что одновременное "встраивание" в ЧЭП двух констант: е и π, предопределит следующие конструктивные её параметры: К(р) = 1,2738; α(р) = 51 градусов 52 минуты. Увеличение же встраиваемой точности числа е до четвёртого знака после запятой, приведёт к росту количества ступенек до 2613.
Подводя итог по конструкции ЧЭП, в том числе и пирамидальных конструкций на базе ЧЭП, можно констатировать, что конструктивно пирамидальные конструкции типа ЧЭП, могут выполняться в виде стоящих друг на друге прямоугольных числовых блоков; блоков, боковые стороны которых наклонены в сторону оси пирамиды.
Вышесказанное в отношении конструкций пирамид на базе ЧЭП, имело место только для пирамид плоского изображения. В случае пространственной форы, в основание ЧЭП необходимо заложить соответствующий многоугольник. Так, при наличии квадрата, пирамида будет правильной, четырёхугольной; шестиугольника, правильной шестиугольной и т. д. Эти формы пирамид следует дополнить пирамидами, в основании которых используется окружность. Такие пирамиды будут называться конусообразными. Все перечисленные пирамиды относятся к разряду "правильных". Это обстоятельство неслучайно и обусловлено тем обстоятельством, что только правильная пирамида "обладает возможностью" воспроизвести в сечении, проходящем через её высоту и две противолежащие апофемы, конструктивные параметры плоской ЧЭП; см. рис. 27; 28. *) Примечание: Апофема − высота боковой грани правильной пирамиды.
ДЕЙСТВИЕ 2.
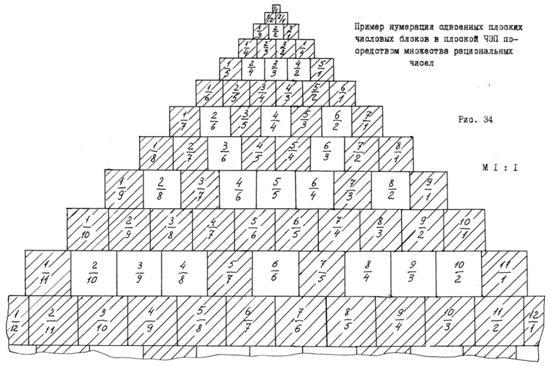
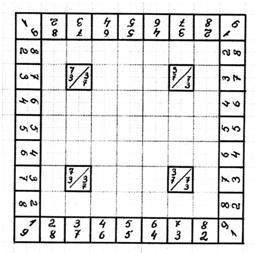
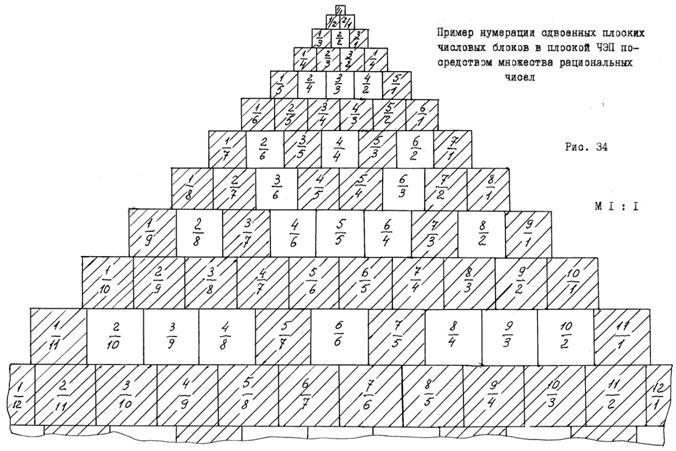
Прономеруем последовательно числовые блоки эквивалентных ступенек ЧЭП, изображённой на рис. 34, слева − направо и одновременно, справа − налево; смотри рисунок:
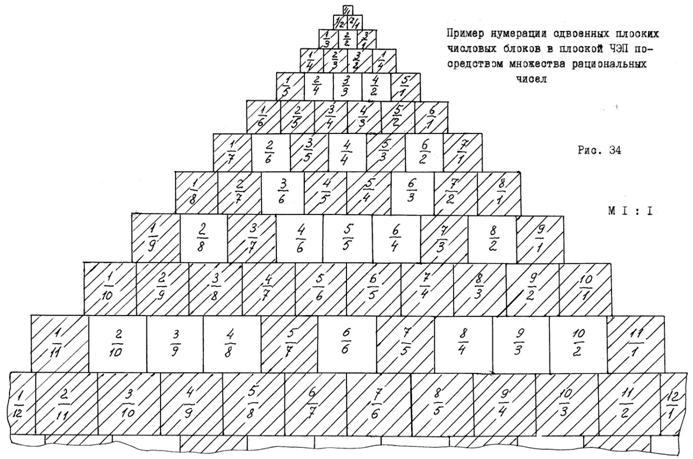
Результат запишем в виде рациональной дроби, который одновременно будет являться и дробным номером числового блока. По этому номеру мы безошибочно можем определить местоположение числового блока в здании ЧЭП. Так, например, блок с номером 7/1 принадлежит 7 −ой ступеньке и располагается в крайней позиции справа. А вот числовой блок с номером 5/4 будет принадлежать уже другой ступени. Для определения его местоположения необходимо предварительно определить номер эквивалентной ступени. Для этого, достаточно сложить числитель со знаменателем дроби и вычесть единицу. В соответствии со сказанным, порядковый номер ступени для блока 5/4 будет 8 −ой, ибо 5 + 4 − 1 = 8. По порядку расположения в ступеньке слева, он будет пятым, а справа четвёртым. На рисунке, этот числовой блок располагается около оси ЧЭП справа. Подобным образом можно определить местоположение любого числового блока в здании ЧЭП.
В случае пространственной ЧЭП, например, ЧЭП (М4) − где М символ квадратной ступеньки, дробную нумерацию блоков осуществим так, как показано на рис. 37; см. рисунок:
Рис. 37.
На этом рисунке, схематично изображена девятая ступенька ЧЭП. Нумерацию наружных эквивалентных блоков осуществим по "кольцевой" схеме (см. рисунок), начиная с "нижнего", крайне левого блока. Внутренние же блоки, обозначим двойной, дробной нумерацией, в двух взаимно перпендикулярных направлениях. По первому направлению, движение по слоям блоков (в плане рисунка) следует осуществлять снизу вверх; по другому, взаимно перпендикулярному, можно "перемещаться" как слева − направо, так и справа − налево. В результате мы получим нумерацию блоков такой, какой она представлена на рисунке. Как будет показано далее, такая нумерация блоков в ЧЭП, нам потребуется для выявления "математических пустот" в пирамиде.
Задав нумерацию числовым, эквивалентным блокам в виде рациональных дробей, мы получили очень важный результат как в плане математическом, так и в конструктивном. Действительно, с позиции Математики, последовательную нумерацию числовых блоков в ступеньках пирамиды, можно трактовать как способ кодирования множества натуральных чисел (N), множеством рациональных чисел (Q). *)
_______________
*) Примечание: По принятому правилу в Математике, множество целых чисел (Q), получается за счёт добавления к множеству натуральных чисел (N) математических объектов − отрицательных чисел и нуля.
_______________
Множество целых чисел (Q), подобно множеству натуральных целых чисел (N), может быть представлено по схеме "квадрата" и графически изображено в плоской, прямоугольной системе координат. В результате получится конструкция в виде двух пирамид ЧЭП, обращённых друг к другу и имеющих одну, общую вершину; см. рис. 35:
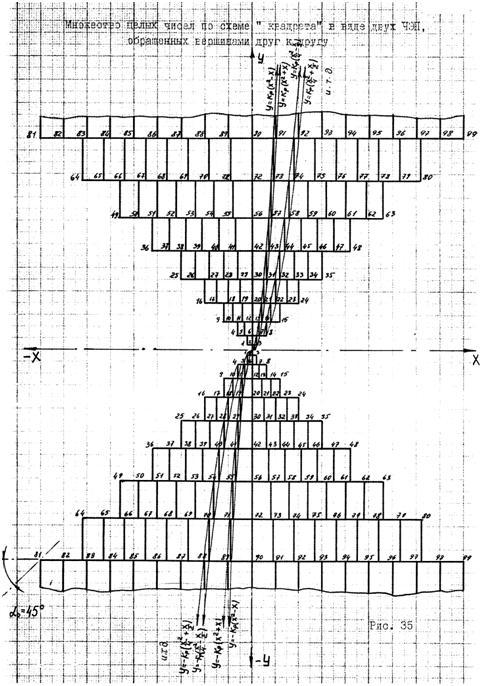
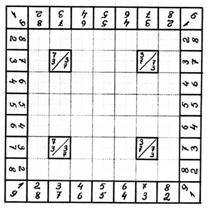
Однако следует заметить, что в операции кодирования множества натуральных целых чисел участвуют не все рациональные числа (дроби), а только те, которые являются несократимыми. Воспользуемся этим правилом и удалим из эквивалентных, числовых ступенек ЧЭП все блоки, имеющие сократимую, дробную нумерацию. В результате внутренняя часть ЧЭП, в конструктивном отношении предстанет перед нами такой, какой она изображена на рисунке 34. На этом схематичном рисунке, "математические" пустоты в ЧЭП, выполнены без штриховки; см. рисунок:
После этого можно сделать (очень важный в математическом и конструктивном отношении) вывод:
любая ЧЭП, в том числе и пространственная, "несущая" в своей конструкции информацию о натуральном ряде целых чисел, представленному по схеме "квадрата", а также информацию о несократимых рациональных дробях, отождествляемых с номером соответствующего числового блока в эквивалентных ступенях, обязательно должна содержать "математические" пустоты в виде прямоугольных (в т. ч. и квадратных) плоских числовых блоков для ЧЭП и прямоугольных параллелепипедов (в т. ч. и кубов), в случае пространственной, правильной пирамиды ЧЭП(М4).
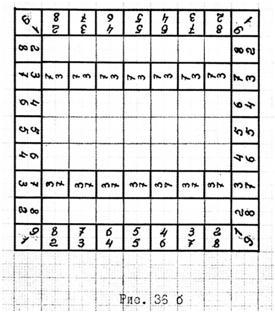
По отношению плоской ЧЭП мы имеем только один конструктивный вариант "математических" пустот. У пространственной ЧЭП(М4), таких вариантов может быть несколько. Разберём их на примере девятой её эквивалентной ступеньке. С этой целью обратимся к рисунку 36:
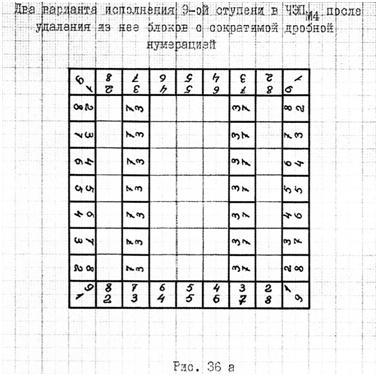
Первый вариант "математических" пустот мы получим, если будем двигаться снизу − вверх (в плане рисунка) и для каждого слоя эквивалентных блоков, кроме наружных, будем выполнять кодирование блоков так же, как и в случае "плоской" ЧЭП. Этот вариант представлен на рис. 36а.
Второй вариант, являющийся подобием первого, мы получим, если будем двигаться слева − направо или справа − налево (в плане рисунка); кодирование блоков произведём так же, как и в первом варианте. Второй вариант можно получить из первого, посредством поворота последнего на 90 градусов по или против часовой стрелки, относительно оси ЧЭП(М4) см. рис. 36б.
Третий вариант мы получим, объединив в один первый и второй. "Проделывание" "математических" пустот осуществим по следующему правилу: наружные эквивалентные блоки, кодируемые по кольцевой схеме, остаются в ступени, а из внутренних удаляются только те, в двойной, дробной нумерации которых имеется хотя бы одна сократимая рациональная дробь. Удалив блоки, в соответствии с этим правилом, из девятой ступеньки ЧЭП(М4), мы получим конструкцию "математических" пустот этой ступеньки такой, какой она представлена на рис. 38; см. рисунок: Рис. 38.
Подобным же образом можно осуществить "проделывание" "математических" пустот, или просто пустот, во всех эквивалентных, числовых ступеньках ЧЭП(М4).
Информация к размышлению:
Так как статья имеет целью (подчёркиваю, в первом приближении) математическое осмысление творения древних зодчих, то наличие вывода о "математических" пустотах и последующих соображений по ЧЭП(М4), позволяет к их творениям (имеется в виду пирамида Хеопса) подойти двояко. С одной стороны, наличие конструктивных пустот в ЧЭП(М4), в натуре подтверждено французскими и японскими учёными, а с другой, перед нами встают два вопроса:
1. Выполнены ли основные конструктивные пустоты в теле пирамиды Хеопса (кроме тех, которые используются для посещений и являются в настоящее время известными) по вышеприведённой схеме кодирования эквивалентных, числовых блоков множеством рациональных чисел?
Каким образом первый вопрос сочетается с принципом разумной достаточности?
Автор имеет в виду следующее: при внимательном рассмотрении оставшихся после удаления из ЧЭП(М4) соответствующих блоков, мы видим (см. рис.34), что некоторые блоки пребывают как бы в "подвешенном" состоянии, например: блоки 3/5; 5/3; 4/5; 5/4; а есть и такие, которые не несут статической нагрузки: например, блоки 5/6; 6/5; 3/10; 10/3; 4/9; 9/4 и т.д.
Учёт принципа "разумной достаточности", требует в конструкции ЧЭП(М4), для первых перечисленных блоков, оставить блок под номером 5/5, для вторых оставить 5/5; 2/10; 3/9; 4/8; 8/4; 9/3; 10/2 и т. д. Ответы на эти вопросы в отношении пирамиды Хеопса, а также подобных других пирамид, дело Будущего. Потому данную информацию читатель может воспринимать как "Информация к размышлению".
А теперь, коротко перечислим сведения из Математики, которые с помощь ЧЭМ(М4) можно "передать" в Будущее.
Сведения:
1. О натуральном ряде целых чисел (N).
2. О ряде квадратов.
3. О числовых подмножествах натурального ряда чисел, структурно строящихся по схеме "квадрата". Эта информация "представлена" самими ступенями ЧЭП(М4).
4. О ряде нечётных чисел, являющихся также подмножеством натурального ряда чисел. Эта информация выявляется при диагональном следовании от чисел (числовых блоков), например, первой эквивалентной ступени, к блокам последующей и т. д.
5. О кривых второго порядка; квадратных уравнениях.
6. О множестве рациональных чисел; представление о правильных и "неправильных" дробях. Эта информация "содержится" в дробной нумерации в числовых блоках ступеней.
7. О возможности кодирования множеством рациональных чисел, множества натуральных чисел.
8. Об Арифметической прогрессии.
9. Об операциях сложения и вычитания. Эта информация "представлена" изменением высот эквивалентных, числовых ступенек. При движении от вершины пирамиды к её основанию, высота ступенек последовательно увеличивается на две единицы; в обратном направлении, от основания пирамиды к вершине, наоборот, их высота убывает на две единицы.
10. О плоской и пространственной системах координат (правда косвенно), соответственно, и о числовых осях.
11. Об угле, высоте, площади, основании, периметре, грани и т. д.
13. О имеющихся в Математике числовых констант π и е − трансцендентных числах, и, следовательно, о пределах.
14. О системе измерений. Система может быть любой, в том числе и метрической. По отношению пирамиды Хеопса известно, что она выполнена в метрической системе, которая была принята во Франции только . . . . в XVШ веке !
15. Наличие метрической системы, предопределяет сведения о 10 −ой системе исчисления.
16. Совмещение понятий целого числа и его дробной части, позволяет, при наличии 10 −ой системы исчисления, перейти к представлению о десятичных дробях и т. д.
Подобный перечень из Математики, можно было бы продолжить и дальше. Однако в нашем случае это не самоцель, а стремление выявить наличие возможности, посредством строения соответствующей формы, передачи во времени математических знаний для последующих поколений в "далёкое" Будущее.
Итак, после всего сказанного выше, можно констатировать, что строение пространственной формы, в виде правильной четырёхугольной пирамиды, элементы которой выполнены по соответствующим математическим закономерностям, позволяет "передавать" в Будущее определённый перечень сведений из Математики. Это обстоятельство, требует совсем иного подхода к творению древних зодчих, к пирамидальным сооружениям. Видно у тех, кто в глубокой древности решился на возведение таких колоссов, как пирамиды Хеопса, Хефрена, Менкаура, храма IV от цивилизации Майя и т. д., были намного более веские причины, нежели те, которые обусловлены лишь погребальными соображениями со стороны фараонов. А вот слияние во временном плане обоих этих начал воедино, было не только правомерным актом, но и просто необходимым явлением, ибо без мощной финансовой и технической поддержки, осуществление подобного грандиозного строительства, тем более в то, далёкое время, не представлялось возможным.
Представляется, что такой подход к проблеме древних, пирамидальных сооружений, а ведь до нас "дошли" сооружения именно этого типа, позволяет приблизиться и к истокам самой пирамидальности, ибо с позиции Математики эта форма является наиболее приемлемой для передачи математических, а возможно и не только их, знаний из далёкого прошлого в Будущее. А от сюда следует, что "истоки" пирамидальности древних сооружений "исходят" из Математики! Будем надеяться, что последующее комплексное исследование пирамидальных сооружений, позволит многое понять в намерениях древних строителей, а пока попробуем, примерно сгруппировать пирамидальные сооружения древности по конструктивному исполнению в отношении к ЧЭП(М).
Анализ имеющихся в печати сведений о пирамидальных сооружениях прошлого, позволяет сделать вывод, что наиболее близкими к ЧЭП(М4) являются пирамиды Египта, расположенные в долине Нила. Из имеющихся здесь пирамид, а на территории современного Египта их открыто около 80 −ти, упомянем следующие:
1. Ступенчатые пирамиды. Наиболее представительной из этого вида, является пирамида Джосера, высотой около 61 метра. Она имеет шесть ярусов и расположена на пустынном плато Саккара, в Нижнем Египте. Такие же пирамиды (гробницы), хотя и в гораздо худшем состоянии, чем пирамида Джосера, сохранились в Завиет эль − Эриане, между Саккарра и Гизе; в Медуме, где один из фараонов, по−видимому Хуни, начал возводить ступенчатую гробницу − позднее Снофру достроил её уже как "настоящую"; в Силе, близ Фаюма; в Завиет − эль − Майитине, в Среднем Египте, а также в Нубте и в Куле в Верхнем Египте.
Этот вид сооружений: и пирамида Джосера, и многослойная пирамида в Завиет эль − Эриане, имеют сходное строение (примечание: двенадцать слоёв каменной кладки с наклоном в 74 градуса внутрь в первом случае, и четырнадцать слоёв с наклоном в 68 градусов во втором). Медумская пирамида имеет такую же конструкцию первой и второй ступени надстройки; соответственно, семь и восемь слоёв кладки с наклоном внутрь с 74 градуса. Первоначальна Мастаба − арабск. букв. − каменная скамья; древн. − егип. гробница /3 −тье тыс. до н. э./в виде лежащего бруса, с наклоном к центру стенами; в подземной погребальной камере статуи, рельефы, росписи) Джосера в Саккара, которая стала основой для последующей постройки, была выстроена независимыми рядами горизонтальной кладки. Сама пирамида Джосера являет собой огромное, центральное сооружение из независимых слоёв кладки, ряды которой наклонены внутрь, с сооружением квадратной формы; окруженным могучей оградой; облицованной высококачественным известняком.
В математическом отношении, пирамиды подобной конструкции следует отнести к пирамидам, которые схематично (в разрезе) представлены на рисунке 29.
В более поздних, так называемых "настоящих" пирамидах, с прямыми, а не ступенчатыми гранями, слои кладки расположены горизонтально. Наиболее крупные из них располагаются на плоскогорье Гиза. Их три: пирамида Хуфу (Хеопса − греч.), Хафра (Хефрена), Менкаура (Микерина). Приблизительные длины сторон основания этих колоссов в метрах, соответственно, равны: 233; 147; 215; 143; 108; 66. По своему конструктивному исполнению, в виде прямоугольных блоков, эти и им подобные пирамиды наиболее близки к ЧЭП(М4), схематично представленной в разрезе на рисунке 33.
Несколько замечаний в отношении пирамиды Хеопса: просматривая материалы в печати, посвящённые архитектуре памятников древнего Мира, автору не удалось найти данные по характеру изменения высоты ступеней пирамиды Хеопса, на протяжении всей её высоты, а также данных о количестве у неё ступеней. Эти данные необходимы для проведения соответствующего анализа на соответствие этой пирамиды пирамиде ЧЭП(М4) с К(р) = 1,2738 и α(р) = 51 градуса 52 минуты. Для неё эти данные можно получить, исходя из сравнительно несложного расчёта, приводимого ниже. При этом можно выделить несколько вариантов:
1. Расчёт, то есть определение высоты первой и нижней ступени пирамиды ЧЭП(М4), количества ступеней и длины нижней ступени, строится из предположения, что характер изменения высоты ступеней пирамиды Хеопса идентичен характеру изменения высоты ступеней ЧЭМ(М4), т. е. высота ступеней, в направлении от вершины к её основанию, возрастает по закону арифметической прогрессии. В соответствии с этим условием, результаты расчёта будут следующие:
1.1. Высота (ориентировочная) пирамиды берётся в соответствии с приводимой в печати высотой пирамиды Хеопса: около 147 м.
Примечание: страницу 96 можно не брать во внимание.


Примечание: в расчёте 2 можно опустить то, что в скобках (см. п.1 на стр.110).

− 905,58684) = 233902,1 = 233,9 м.
Сравнение полученных результатов по отношению к длине стороны нижней ступени (основания) пирамиды Хеопса, указывает на то, что наиболее близким к этому показателю (233 м.) является результат пункта 1.
После этого, в свете полученных результатов, можно констатировать следующее:
если древние строители, стремились в пирамиде Хеопса воплотить конструктивные элементы ЧЭП(М4), в соответствии с расчётом п.1 и п.2, то в элементах её конструкции они "заложили" данные п.1 и п.2. При этом в первом пункте, основное внимание сосредоточено на характере изменения высоты ступеней по закону Арифметической прогрессии, т. е. выделяется сам факт наличия в Математике подобного объекта. Постоянной же е , трансцендентному числу, в этом варианте отводится второстепенная роль. Если же в пирамиде Хеопса воплощён второй вариант, то тем самым, мы можем констатировать факт выделения в первую очередь трансцендентного числа е, как одной из замечательных констант Математики.
Какой из этих вариантов был воплощён в действительности, покажут вероятно будущие исследования. И всё же следует выказать следующее соображение:
в соответствии с первым вариантом расчёта, высота каждой последующей ступени, по отношению предыдущей, возрастает на d = 2,5476 мм. и так на протяжении всей высоты ЧЭП(М4). Представляется очень трудным, в условиях того времени (? . . . ), по все высоте пирамиды выдержать эту разницу высот ступеней. Во втором варианте расчёта, этот фактор отсутствует, что значительно упрощает технологию изготовления блоков и т. д. С этих позиций, этот вариант, являющийся унифицированным вариантом, намного предпочтительнее первого.
С другой стороны, оба варианта существенно разнятся по количеству блоков, требуемых для строительства ЧЭП(М4), пирамиды Хеопса. Без учёта "математических" пустот, в теле пирамиды (примечание: это будет сделано ниже), общее количество блоков можно подсчитать по формуле конечной суммы числового ряда
В результате, мы получим следующий результат:
для n = 341

Наиболее близким к данным, приводимым в печати (около 2300000 блоков в пирамиде Хеопса), является второй вариант. Однако, если она в действительности содержит около 2300000 блоков, то из вышеприведённой формулы числового ряда следует (без учёта "математических" пустот), что у неё должно быть 190 ступеней. В общей сложности, для такой ЧЭП(М4), необходимо 2304415 блоков, высотой 0,774 м.
А теперь рассмотрим вопрос о наличии в теле ЧЭП(М4) конструктивных, "математических" пустот. Для этого обратимся к плоской, ступенчатой пирамиде на рисунке 39:

Эта пирамида, в конструктивном отношении выполнена с учётом удаления из её ступенек плоских, квадратных блоков, с сократимой дробной нумерацией. Эту пирамиду можем классифицировать по Варианту 2, для которой основным признаком является одинаковость высоты эквивалентных ступенек. На рисунке видно, что отдельные плоские блоки выделены красным цветом. Эти блоки имеют "дробную", сократимую нумерацию. Однако, как было отмечено выше, отдельные блоки с такой нумерацией, необходимо оставлять в здании пирамиды. Их количество для каждой ступени, выбрано минимальным.
На примере этой, плоской пирамиды (для случая n = 165) можно подсчитать процентное соотношение между "математическими" пустотами и блоками. Для этого воспользуемся нижеприводимой формулой, позволяющей производить подсчёт количества пустотелых блоков в отдельно взятой ступеньке пирамиды ЧЭП(М4) на примере её плоского варианта ЧЭП:

Эту формулу можно записать несколько иначе:
Q{М4(Љ ст.)} = Q(Љ ст.) • {(2Љ ст.) − 4 − Q(Љ ст.)}, где: (8)
Q{М4(Љ ст.) − количество пустотелых блоков, в соответствующей ступеньке правильной, четырёхугольной пирамиды ЧЭП(М4);
Љ ст. − номер ступеньки пирамиды;
Q(Љ ст.) − количество пустотелых блоков в одноимённой ступеньке плоской пирамиды.
Для примера, произведём подсчёт количества пустотелых (в математическом отношении) блоков на примере девятой ступеньки. Для этого, необходимо подсчитать количество пустотелых блоков (см. рис. 39) в одноимённой ступеньке в плоской пирамиде. Их количество равно четырём. Подставляя число 4 в формулу 8 и произведя подсчёт, получим: Q{М4(9)}мин. = 4( 2 • 9 − 4 − 4) = 40.
Сравни полученный результат с рисунком 40: Рис. 40. " weight="500" height="300" align="middle" vspace="1
Из предыдущего расчёта видно, что расчёт производился по схеме минимального удаления блоков с сократимой дробной нумерацией и, потому, его можно условно считать расчёт по минимуму. В противном случае, когда в расчёт берутся все блоки с сократимой, дробной нумерацией, его можно именовать как расчёт по максимуму. В соответствии с этим расчётом, общее количество пустотелых блоков в девятой ступеньке правильной ЧЭП(М4) будет: Q{М4(9)}макс. = 5(2 • 9 − 4 − 5) = 45. Схема расположения блоков в соответствии с этим результатом, представлена на рисунке 38: Рис. 38.
После этого, если произвести подсчёт пустотелых блоков в правильной, четырёхугольной пирамиде по минимуму для n = 165, то найдём, что их общее количество составит 697530 шт. В процентном отношении − это количество блоков, по отношению к 1511015 блокам (см. выше) составляет 46,16%. В случае расчёта по максимуму общее количество пустотелых блоков составит 827265 шт. В процентном отношении к 151015 блокам, это составит 54,75%.
К полученному математическому результату можно относиться по разному: и чисто теоретически, и чисто практически. Однако, если в расчёт брать одновременно оба этих подхода, то должны будем констатировать следующее:
знание теоретической стороны данного вопроса, предопределяет снижение "соответствующих" затрат при возведении данной или подобной ей пирамиды в натуре. Соответственно, сокращаются и сроки самого строительства.
Эта констатация, позволяет исследователям древних пирамидальных сооружений, в действиях строителей видеть не только разумное начало, но и заведомо ожидать открытие новых, ещё неизвестных пустот в подобных сооружениях, в том числе и в пирамиде Хеопса. По крайней мере, последние предположение было подтверждено на примере пирамиды Хеопса исследованиями французских и японских учёных.
Логическим продолжением, в конструировании пустотелых пирамид служит мысль о том, что количество пустот в пирамиде можно довести до такого количества, когда в здании пирамиды, наряду с внешними блоками, заложено минимальное количество и несущих, внутренних блоков. Идея сводится к тому, что по высоте пирамида делится ступеньками, не имеющих пустотелых блоков, на промежутки. В подобных промежутках, отдельные блоки сгруппированы в виде небольших пирамидок, выполняющих как бы роль несущих опор. При этом одни располагаются основанием вниз, а другие вверх. Удалим последние из здания пирамиды. В результате появляется возможность "заложить" в конструкцию пирамиды пустоты внушительных размеров. Один из таких возможных вариантов, представлен на рисунке 41: Рис. 41. *)
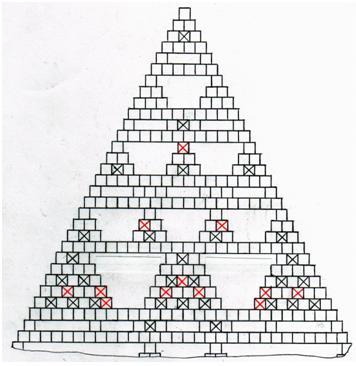
*) Примечание:
1. Квадрат с красным крестом − плоский блок с дробной нумерацией, оставляемый в здании пирамиды;
2. Квадрат с чёрным крестом − плоский блок с дробной нумерацией, подлежащий удалению из здания пирамиды.
_______________
Так, для примера, высота пустот между 112 и 120 ступенями составит 7 • 147 • 165 = 6,236363 метра. Здесь число 7 − это количество ступеней между 112 и 120 ступенями; 147 − размер высоты пирамиды в метрах; 165 − количество ступеней в пирамиде; − (примечание: за основу взят вариант пирамиды Хеопса с 165 ступеньками одинаковой высоты).
Наличие подобных пустот в теле пирамиды, с одной стороны, позволяет использовать их, например, в качестве погребальных камер и проходов к ним (это один из возможных вариантов), а с другой, налицо дополнительные трудности при строительстве подобной пирамиды в натуре. Так, для поддержания потолочных блоков − блоков в сплошных ступенях, не являющихся монолитом по всей лине (площади, в пространственном варианте), необходимо использовать соответствующие потолочные балки или фермы. Из практики современного строительства известно, что в качестве таковых используются деревянные или металлические конструкции (в том числе армированный бетон в виде потолочных плит). Но всем этим материалам присущ один, общий недостаток − недолговечность. А как показывает практика, именно этот фактор является основополагающим в строительстве пирамидальных сооружений прошлого.
Эта, на первый взгляд непреодолимая трудность, преодолевается просто, если при строительстве подобного пирамидального сооружения выдвинуть два требования:
1. Все сплошные ступени, по всей высоте пирамиды, выполнить монолитными. Это требование предопределяет монолитную связку блоков по их боковым поверхностям или делать эти ступени . . . . . из бетона.
2. В качестве дополнительных несущих опор, взамен удаляемых блоков из пространства между сплошными ступенями, использовать широко применяемую на практике строительства песочную подушку.
Из этих двух требований последнее является наиболее оптимальным, ибо позволяет до минимума свести потребное количество блоков для возведения пирамиды и, тем самым, сократить сроки её строительства. Одновременно с этим вырисовывается и место возведения пирамиды: при прочих соответствующих требованиях, в месте строительства пирамиды должно быть достаточное количество песка. В результате мы приходим к выводу, что наилучшим местом, удовлетворяющим этому требованию, является полупустыня или окраинная часть пустыни, где в избытке имеется песок и нужная для строительства вода. В подтверждение сказанного, можно привести результаты исследований пирамиды Хеопса французскими и японскими учёными: при бурении в одной из вновь открытых пустот, был обнаружен песок с вкраплинами раствора. Как показали исследования, этот песок добывался в шести километрах юго − западнее самой пирамиды.
3. Пирамидальные сооружения, имеющие явно вычленяемую конструкцию; см. схематичные рисунки 31 ÷ 32. К числу таковых следует отнести индийскую пагоду в Индии, выполненную в виде пустотелых железных кубов, стоящих друг на друге, а также ряд пагод в той же Индии, Бирме, Китае и т. д. Сюда же следует отнести и суданские пирамиды, возведённые древними нубийскими строителями. Для этих пирамид характерен более крутой угол наклона боковых граней (αр). Так, архитектор из Германии(в прошлом из ГДР) Фридрих Хинкель, с 1976 года работающий над реставрацией памятников древности на территории Судана, показал, что боковые грани на чертеже наклонены к вертикали под углом 72 градуса 45 минут, а в натуре этот угол (αр) составляет 72 градуса 48 минут, т. е. шибка менее 0,1%. Погрешность, допущенная в длине сторон основания пирамиды, составила около 1%.
Кроме названных конструкций, к этому пункту следует причислить и те пирамидальные сооружения, боковые грани которых выполнены по одной из кривых второго порядка, а в сечениях, параллельных основанию пирамиды, располагается квадрат или окружность. Здесь можно указать на массивную, бежевого оттенка мечеть в городском ландшафте Джене (Мали). Имеются подобные здания в Южном Йемене и в Бирме, например, комплекс Шуэдагоун − величайший памятник средневековой архитектуры в Рангуне. В Индии же имеется экспонат древности − нержавеющая колонна, отлитая индийскими мастерами (предположительно) ещё в V веке. Расположена она рядом со стенами знаменитого Кутб−Минара (Башни Победы). У этого памятника древности, наружный профиль по высоте выполнен по кривой соответствующего порядка, а в сечении, перпендикулярном высоте, заложена окружность.
4. Конусообразные пирамидальные сооружения, имеющие, в сечении перпендикуляром высоте сооружения, окружность. К числу таковых, следует отнести, разнообразные по конструкции, пагоды Азиатского региона.
5. К этому пункту мы причислим остальные сооружения, планировка которых на местности, расположение внутренних и внешних стен ограды относительно друг друга, выполнены по схеме пирамидальных сооружений. Для примера, можно указать комплекс Ангкоровата − одного из шедевров мирового зодчества, возведённого на северо − западе Кампучии более восьми столетий назад; (см. газету "За рубежом" Љ 47 за 1987 г., стр. 23). Сюда же следует отнести, например, и памятник эпохи первобытно − общинного строя Индонезии − огромная многоступенчатая пирамида Боробудур, возвышающаяся в центре острова Ява и т. д.
Как видно из вышеприведённого, далеко неполного перечня пирамидальных сооружений, "выпали" пирамиды и пирамидальные сооружения Американского континента. Их конструктивные формы принципиально отличаются от подобных сооружений в Старом свете. Так, например, на центральной площади Тикаля − один из крупнейших городов древней цивилизации Майя, расположен на территории департамента Петен в современной Гватемале, возвышается пирамида, вершину которой венчает храм Ягуара. Конструктивно пирамида выполнена в виде трёх больших ярусов, сужающихся в направление к вершине, и крутой лестницы, с большим количеством ступенек; её высота около 50 метров. В общем, сооружений подобного типа, на территориях различных государств, насчитывается немало. Однако всем им присущ сугубо местный конструктивный колорит, позволяющий выделить их в отдельную группу пирамидальных сооружений. Смотри, например, ниже вырезки из газет:


В то же время, учитывая почтенный возраст пирамид и Нового, и Старого света, вправе поставить следующий вопрос: "Имеют ли те и другие пирамиды общую конструктивную "природу" и если да, то на чём она базируется?" Не исключено, что постановка данного вопроса, вызовет у читателя недоумение: ведь одного взгляда достаточно, чтобы утверждать "обратное". Однако не будем, столь категоричными, и попробует при ответе на данный вопрос, подойти с позиции Математики. А для того, чтобы ход рассуждений был более понятен читателю, мы, с одной стороны, обратимся к технологии возведения ЧЭП(М4), а с другой, к тому, что нами из Математики задействован сравнительно небольшой перечень сведений.
В отношении технологии возведения пирамиды, с наличием в ней соответствующих, конструктивных пустот, можно выделить два основных момента:
1. ЧЭП(М4) строится из каменных, предварительно изготовленных в каменоломне, блоков. При этом не исключается возможность их укрупнения в блочные плиты до размеров, определяемых возможностью их транспортировки до места строительства.
2. ЧЭП(М4) строится из блоков соответствующего бетонного раствора. Изготовление блоков может производиться в опалубку, на месте их расположения в здании пирамиды, или же изготовляться в подходящем для этого месте, с последующей их транспортировкой к месту строительства.
В отношении этого пункта следует отметить, что согласно последних исследований пирамиды Хеопса, она сложена из бетонных монолитов. В настоящее время эта версия имеет немало приверженцев в среде учёных. По этому поводу в "Комсомольской правде" от 27 декабря 1987 г., в заметке "Пирамиды из бетона?" сообщалось, что ". . . американский химик, профессор Бернского университета Джозеф Давидович . . . , анализируя химический состав "монолитов", из которых сложены пирамиды, пришёл к неожиданному выводу: это бетон! Давидович определил 13 компонентов, из которых он мог изготовляться. В одной из пирамид найдены следы опалубки, которая обычно остаётся при бетонировании. А несколько дней назад, агенство ЮПИ принесло известие, что Давидович предъявил научному миру, на сей раз неоспоримое доказательство своей гипотезы. В расшифрованной им иероглифической надписи на одной из стел эпохи фараона Джосера (когда была построена первая гигантская усыпальница) содержится подробный рецепт приготовления древнего бетона".
На такой же точке зрения "стоит" и французский химик Д. Девидсон. Состав бетона − измельчённый известняк, смешанный с минеральным вяжущим (вроде цемента) веществом. Его гипотеза объясняет, почему в осколках камня, взятого с пирамид, обнаруживаются минеральные включения и воздушные пузырьки, которых нет в известняке, добываемом в близлежащих каменоломнях: египетские пирамиды построены из известняка, включающего преимущественно раковины нуммулитов, крупных фораминифер. См. заметку "Одноклеточные скваттеры", в рубрике: Биология, Новости науки, ж. "Природа" Љ 3 за 1992 г., стр. 112. Понятно также, почему каменные блоки, как обычно пишут: "так точно и плотно пригнаны друг к другу, что между ними нет ни малейшего зазора". Объясняет гипотеза и ещё одну загадку древности: пирамида Хеопса строилась в 2600 году до н. э. (? . . ), а бронзовые орудия, имеющие достаточную для обработки камня твёрдость, появилась только спустя 800 лет; см. заметку "Пирамиды построены из бетона?", газета "Труд" Љ 209 от 12 сентября 1985 г.
В подтверждение данных гипотез приведу информацию об использовании бетона для строительства в ещё более глубокой древности, нежели во времена строительства пирамид на плато Гиза. Так, на севере Ирака, в районе подверженном землетрясениям, наводнениям и прочим бедствиям, обнаружено здание из каменных плит, скреплённых бетоном. Возраст здания более 7 тысяч лет, что почти вдвое превышает возраст пирамиды Хеопса; см. рубрику "Интеркурьер" в газете "Советская Россия" Љ 85 за 12 апреля 1987 г.
Говоря о технологии возведения ЧЭП(М4), необходимо отметить следующую технологическую трудность: необходимо, чтобы каждый раз высота вышестоящей ступени, по отношению предыдущей, в направление к вершине пирамиды, убывала на одинаковую единицу длины, в соответствии с изменением высоты ступенек по закону Арифметической прогрессии. Для ЧЭП(М4), условного математического аналога пирамиды Хеопса, когда число ступеней равно 338, такой единицей длины является величина d =2,5478 мм. Эта технологическая трудность вполне преодолима, если при строительстве ЧЭП(М4) использовать блоки одинаковой высоты, т. е. строить пирамиду в соответствии с Вариантом 2. В результате появляется возможность от ЧЭП(М4) перейти к пирамидам, которые, наряду с вышеуказанными математическими сведениями (см. выше) содержат и другие, как, например сведения о степенях, логарифмических системах исчисления, о биноме Ньютона, функциях и т. д. Как будет показано далее, именно пространственная интерпретация бинома Ньютона, в совокупности с логарифмической системой, позволила в первом приближении подойти к пониманию конструктивного замысла древних строителей пирамид Американского континента.
БИНОМИНАЛЬНАЯ ЧИСОВАЯ ПИРАМИДА (БЧП).
В буквенном выражении, бином Ньютона записывается следующей формулой:
А теперь, как и в случае с ЧЭП, всю эту информацию объединим в таблицу, записывая для каждого целочисленного значения с соответствующую структуру числовой матрицы в виде многочлена (или бинома Ньютона); см. табл. 13:
