https://t-nauka.ru/wp-content/uploads/k38.pdf c7-18
Полный текст статьи будет размещён на портале eLibrary
Эксперимент с частицами, описываемыми теориями с дополнительными переменными. Подобие эксперимента Алена Аспекта
![]()
![]() (5)
(5)
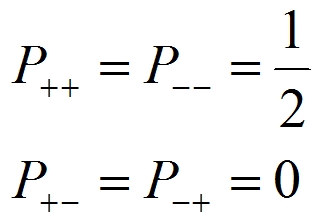
![]()
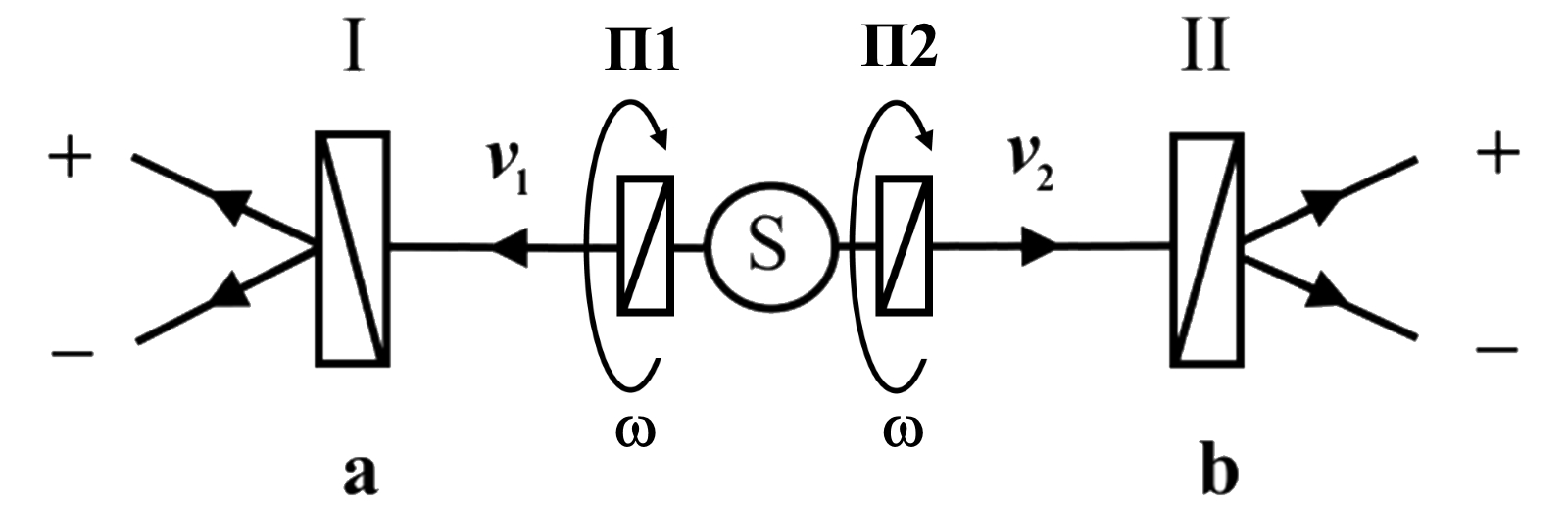
![]()
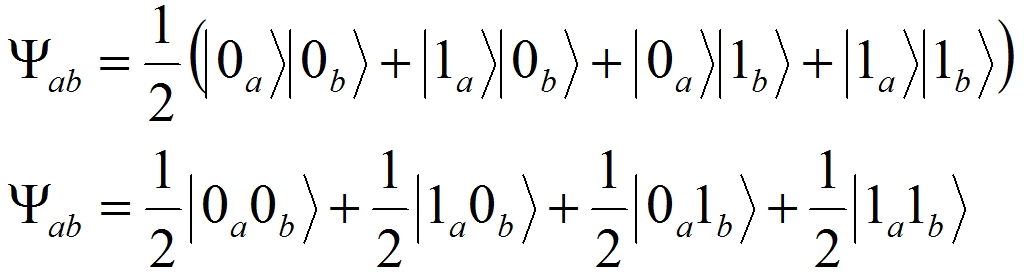
![]()
![]()
![]() (6)
(6)
![]() (7)
(7)
![]()
![]()
![]()
![]() (8)
(8)
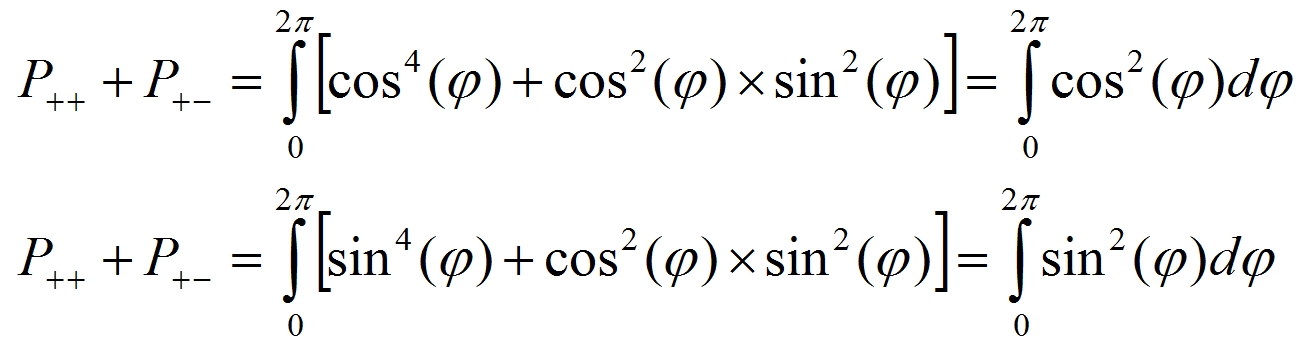
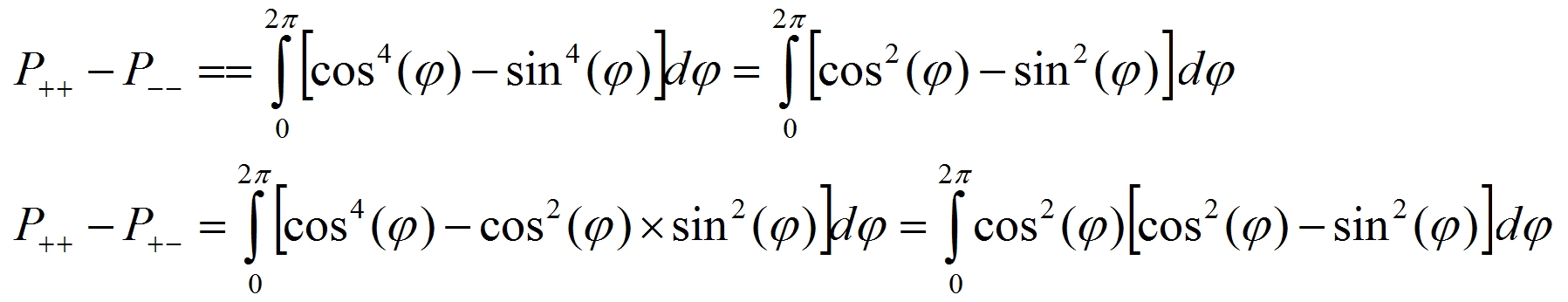
![]() (11)
(11)
![]()