
Рисунок из работы [56]
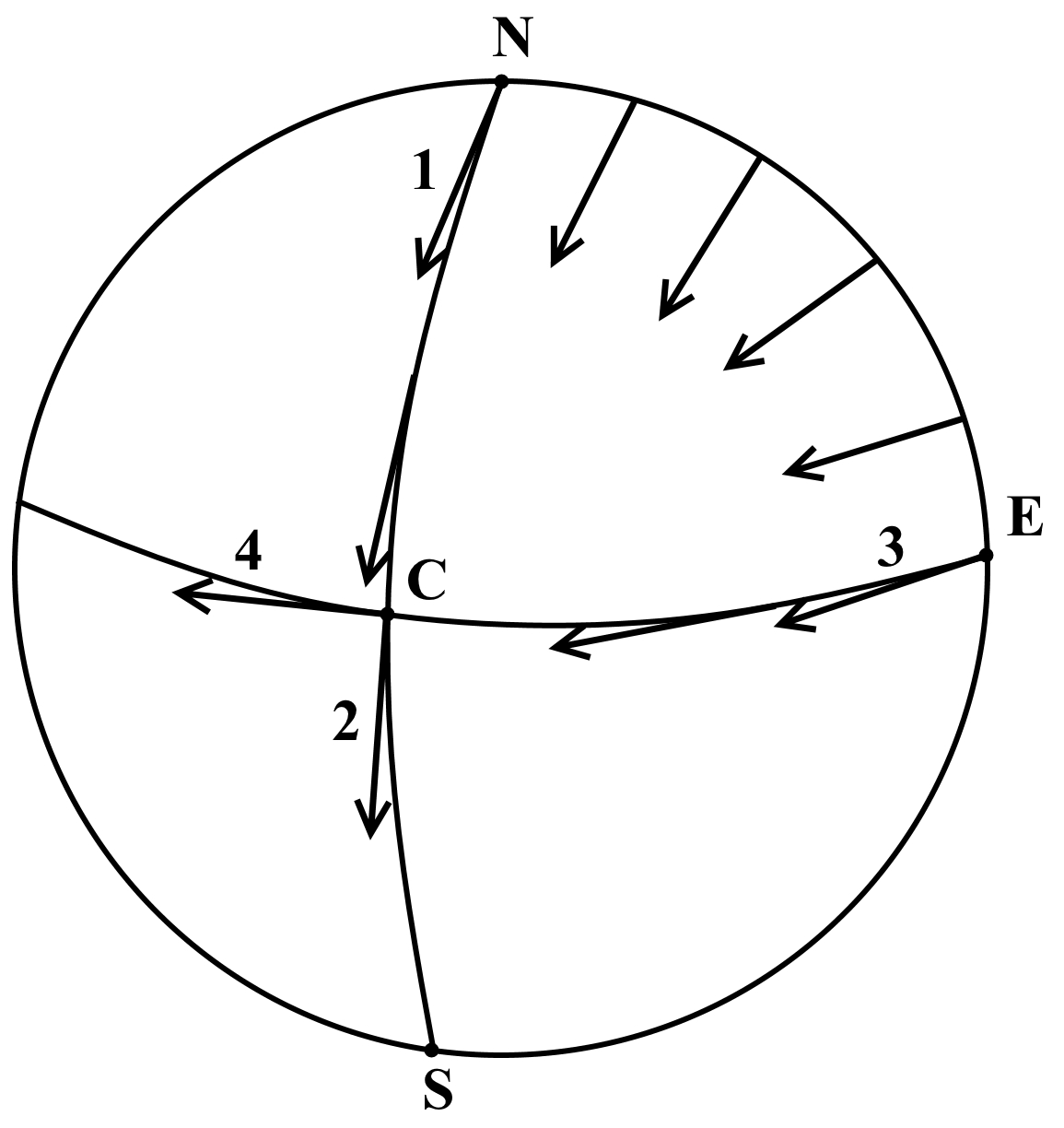
Рисунок, иллюстрирующий зависимость параллельного переноса от траектории в искривленном пространстве [1, с.248]
|
|
||
В искривленном пространстве отсутствует понятие параллельных линий. Под параллельным переносом вектора подразумевается эквиугловой перенос, то есть, перенос с сохранение угла между вектором и геодезической переноса. Paradoxes of parallelism. In curved space, there is no concept of parallel lines. Parallel translation of a vector means equiangular translation, that is, translation with preservation of the angle between the vector and the translation geodesic | ||

Рисунок из работы [56]

Рисунок, иллюстрирующий зависимость параллельного переноса от траектории в искривленном пространстве [1, с.248]