Путенихин Петр Васильевич. Парадоксы параллельности. Часть 2

Оглавление

2. Произвольная траектория в роли геодезической

Перенос вектора по поверхности конуса

Заключение

Литература

2. Произвольная траектория в роли геодезической

Как видно, в некоторых из приведённых цитатах [39], перенос векторов производится по неопределённой траектории, пути, без упоминания, что траектория является геодезической. Насколько это важно? Зависит ли поведение переносимого вектора от характера траектории? Для того чтобы внести определённость в этот процесс:

"... полезно рассмотреть ... внутреннюю геометрию обычной двумерной сферы S². Выберем на S² некоторую точку р (например, для определенности, на северном полюсе) и некоторый касательный вектор v в точке р (направленный, например, вдоль Гринвичского меридиана" [45, с.261].

Сразу же отметим, что выбранный вектор v не принадлежит поверхности сферы, а точки p и q, судя по рисункам к цитате, обе лежат на выбранном меридиане.

"Какие другие касательные векторы в других точках сферы S² мы должны считать "параллельными" вектору v?" [там же].

Именно это и является главным вопросом определения параллельности. В цитате отмечается различие этого понятия на сфере и на плоскости:

"Если воспользоваться евклидовым понятием "параллельности", унаследованным от стандартного погружения S² в евклидово 3-пространство, то мы найдем, что в большинстве точек q сферы S² не существует касательных векторов к S², которые были бы "параллельны" вектору v в указанном смысле, поскольку касательная плоскость в точке q, как правило, не содержит направления v" [там же].

Отметим смягчающие замечания "в большинстве случаев" и "как правило". Это значит, что такие касательные параллельные векторы есть. Вместе с тем, поскольку рассматривается сфера, то указания "в большинстве точек" и "как правило" выглядят чрезмерно осторожными: по сути, это очевидно. Следующее пояснение, хотя и несколько замысловатое для очевидности, но является верным:

"Точки, в которых имеются касательные векторы к S², могущие быть "параллельными" вектору v в этом смысле, содержит лишь большая окружность, проходящая через точку p перпендикулярно к Гринвичскому меридиану" [там же].

Все векторы на указанном ортогональном меридиане, большой окружности и ортогональные к нему, параллельны вектору v в евклидовом 3-пространстве погружения. Все эти векторы и вектор v ортогональны к плоскости описанного фактически "большого круга", круга, образованного этой большой окружностью, содержащей Гринвичский меридиан.

"Подходящее понятие параллелизма на S² должно относиться только к касательным векторам, поэтому лучшее, что мы можем сделать, - это переносить направление вектора v в тангенциальную плоскость в точке q по мере постепенного удаления точки q от p" [там же].

Довольно замысловатое описание процесса вращения вектора v в процессе его удаления от полюса. У понятия "тангенциальная плоскость", популярного в деревообработке, есть синоним: "касательная плоскость". И вновь обратим внимание на противоречие: параллелизм на S², то есть, на поверхности сферы, отнесён к касательным векторам, которые этой поверхности не принадлежат. На рисунках это отчётливо показано: все вектора находятся, изображены на рисунках за пределами поверхности сферы. Фразу "переносить... в тангенциальную плоскость", видимо, следует чуть подправить: не "переносить в плоскость", а "переносить вместе с этой плоскостью", закрепив вектор в исходной тангенциальной плоскости, которую затем и переносим.

"Эта идея прекрасно работает, но теперь возникает новая особенность: вводимое таким образом понятие параллелизма зависит от пути, по которому точка q смещается от точки p" [там же].

Идея прекрасно работает, но с чем? Такой перенос вектора - это перенос в евклидовом трёхмерном пространстве погружения, но никак не по поверхности сферы. Введённое понятие параллелизма - это традиционное, известное понятие для плоского пространства. А особенностью его является то, что перенос вектора не является параллельным по определению, приведённому в цитате. Касательный вектор v изначально определён, постулирован как вектор в пространстве погружения. Перенос, вращение касательной плоскости не имеет абсолютно никакого отношения к событиям на поверхности сферы. Обитатели этого двухмерного мира сферы не могут увидеть ни эту касательную плоскость, ни вектор, в ней лежащий. Видят они лишь одну единственную точку: точку касания. То, что эта точка движется по поверхности сферы, этим обитателям не несёт абсолютно никакой информации. Единственное, что они видят: это линия, нарисованная в их мире. Меридианная линия.

Нет, представленную идею следует признать ошибочной. Возникшая особенность состоит более в ином: параллельный перенос не относится к исходному вектору. Кроме того, эта идея косвенно не только не проясняет, а вообще ставит под сомнение саму идею параллельного переноса.

Для пояснения приводится ещё один рисунок, выполненный, следует заметить, несколько странно, даже небрежно. В цитируемой работе на рисунке рис.14.2б, который мы не приводим, изображена волнообразная кривая линия γ, начинающаяся на северном полюсе и доходящая почти до экватора.

"Рассмотрим кривую γ на S², начинающуюся в точке p и заканчивающуюся в некоторой другой точке q на S²" [45, с.262].

Небрежность состоит, в частности, в том, что на этом рисунке упомянутая точка q не показана. В подписи к рисунку говорится:

"... будем двигать вектор v вдоль заданной кривой γ, постоянно проектируя его на касательную плоскость к сфере. (Полагаем, что кривая γ построена из большого числа мелких отрезков p₀p₁, p₁p₂, p₂p₃, ... , проектируемых на каждой стадии)" [там же].

Здесь также видна неточность: на кривой γ указанные мелкие отрезки не отмечены, отмечены они на находящемся рядом меридиане. Но мы догадываемся, где находятся эти отрезки. Кроме того, пока из пояснения неясно, зачем при переносе вектора v мы постоянно проектируем его на касательные плоскости. И в чём состоит смысл "отрезков... проектируемых"? То есть, на касательную плоскость проектируются как векторы, так и криволинейные отрезки, соединяющие его промежуточные положения? Но что это даёт?

"Затем переходим к пределу, в котором отрезки становятся все меньше"[там же].

Переход к пределу понятен: "ломаные" отрезки превращаются в плавную кривую, не понятно лишь, что это дало.

"Такое понятие параллельного переноса показано на рисунке для Гринвичского меридиана, а также для кривой общего вида γ" [там же].

Похоже на заключительный вывод, завершение пояснения. Однако показанное на рисунке понятие "параллельного переноса" заявленного исправления положения не достигло. Касательные векторы на рисунке по-прежнему принадлежат евклидову пространству погружения E³, а не S² пространству сферы. Косвенно это отмечено чуть выше:

"а) Непосредственное применение евклидовой "параллельности", когда сфера S² считается погруженной в пространство Е³, не работает (за исключением направления вдоль меридиана, перпендикулярного Гринвичскому), поскольку векторы, параллельные v, не остаются касательными к S²" [там же].

Но и здесь утверждение "за исключением меридиана" - тоже не работает. Во всех случаях, включая направление, ортогональное Гринвичу, переносимые векторы не принадлежат поверхности сферы. Далее в тексте приводится более подробное пояснение, повторяющее подпись к рисунку. Интерес представляет следующий фрагмент:

"Будем передвигать вектор v вдоль γ, причем на каждом из отрезков p_r-1p_r перемещать его параллельно самому себе (в обычном смысле, с использованием евклидова трехмерного пространства), а затем проектировать на касательное пространство в точке р_r" [там же].

Мы с неизбежностью трактуем фрагмент цитаты "параллельно самому себе ... евклидова трёхмерного пространства" буквально: касательный вектор v перемещается непосредственно в евклидовом, плоском трёхмерном пространстве погружения E³. Вектор не принадлежит поверхности, пространству S² сферы. Далее следует не менее странная процедура: не принадлежащий сфере вектор проецируется на не принадлежащую сфере касательную плоскость. Всё это происходит вне двухмерного пространства сферы, все эти события не имеют к пространству, миру плоскости сферы никакого отношения. Параллельны переносимые вектора друг другу или нет, для двухмерного пространства сферы не имеет никакого значения. Всё, что у этих миров общего - это единственная касательная точка вектора и плоскости к поверхности сферы, лишь одна общая точка.

"Эта процедура заканчивается касательным вектором в точке q" [там же].

Здесь следовало бы более определённо указать: конечный вектор является касательным к линии на сфере или находится в касательной к ней плоскости, поскольку рассматривались обе ситуации. Также отметим, что здесь нет никаких указаний на то, что произвольная линия переноса вектора обязательно должна состоять из отрезков геодезических, если не считать описанную выше процедуру укорачивания не определённых отрезков.

Приведённый анализ в общих чертах повторяет, дополняет исследования, проведённые в первой части нашей работы. Здесь, в рассмотренных цитатах мы хотим отметить другое, не менее, если не более важное обстоятельство: это разбиение линии переноса на отрезки.

"Полагаем, что кривая γ построена из большого числа мелких отрезков p₀p₁, p₁p₂, p₂p₃, ... , проектируемых на каждой стадии... Затем переходим к пределу, в котором отрезки становятся все меньше" [там же].

Автор цитируемой работы не указывает, с какой целью сделана эта аппроксимация, но по внешнему виду она выглядит традиционной. А именно: любую, произвольную линию на сфере мы можем аппроксимировать короткими, в пределе бесконечно малыми отрезками геодезических, вследствие чего результирующая линия в некотором смысле сама становится подобием геодезической. Но здесь возникает очевидная проблема: теперь невозможным становится не только параллельный перенос вдоль такой "геодезической", а и эквиугловой перенос. Изломы на такой псевдо-геодезической становятся бесконечно близкими и при переходе с одного бесконечно малого участка такой ломано геодезической на следующий частный поворот переносимого вектора становится также бесконечно малым. Другими словами, бесконечном малым становится и изменение угла в процедуре эквиуглового перемещения. Визуально показать это изменение на рисунке просто невозможно. Вместо этого возникает ложное представление об эквиугловом перемещении. Такая аппроксимация является опасной процедурой. По сути, произвольная кривая превращается в геодезическую, хотя и составную.

В случае сферического геодезического треугольника обычно изображается "параллельный" перенос вектора, вектор в конце обхода меняет своё направление. Но что будет, если взять сферически квадратный или прямоугольный контур и использовать "геодезическую" аппроксимацию его изначально не геодезической стороны, параллели? Поскольку мы вправе произвести параллельный перенос вектора по произвольному маршруту, то мы добавили такой отрезок, превратив сферический треугольник в сферический квадрат (вернее, криволинейный четырехугольник). Как видно на рис.2 при таком эквиугловом переносе итоговый угол φ = 0, что означает отсутствие кривизны поверхности.

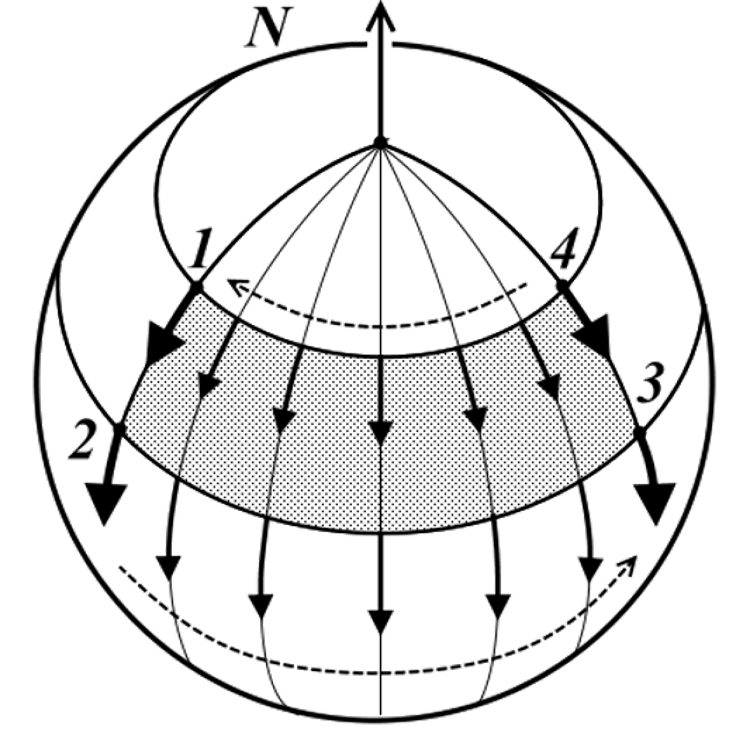
paraldox2

Рис.1. Параллельный перенос вектора на сфере с использованием аппроксимированной геодезической

Однако поверхность сферы определённо является искривленной. Следовательно, такой метод "спрямления" параллели до геодезической неверен или, по меньшей мере, не должен использоваться при графической демонстрации эквиуглового перемещения.

Рассмотрим еще один пример перемещения вектора по произвольной кривой, то есть, кривой, которая не обозначена явно как геодезическая или состоящая из отрезков геодезических. Приведён соответствующий рисунок плавной замкнутой кривой с картофелеобразным контуром, не имеющим явных признаков геодезической (отрезков меридианов, больших кругов).

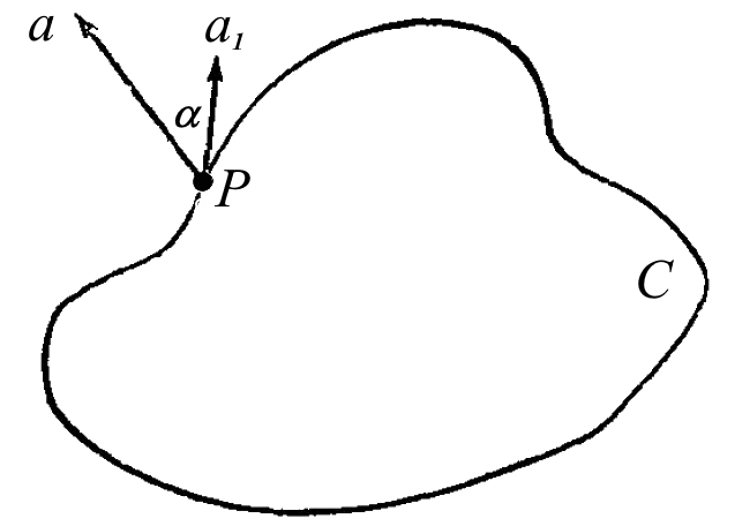
paraldox2

Рис.2. Рисунок 13 из статьи [58]

Рассматриваемые в тексте кривые линии названы прямыми, то есть, имеющими смысл геодезических. В описании рисунка сказано:

"Проведем через заданную точку P. какую-либо замкнутую линию - контур C (рис.13), возьмем некоторый бесконечно малый вектор a в точке P и будем параллельно перемещать его вдоль по линии C, пока снова не вернемся в исходную точку P; наш вектор превратится в вектор a₁, причем ... по направлению ... вектор a, вообще говоря, не должен совпасть с вектором a₁"[58, с.40].

Отметим мягкость заключения: "вообще говоря, не должен совпасть". Нас интересует именно этот вариант "параллельного" переноса векторов, при котором после обхода контура вектор всегда меняет своё направление. Таким свойством обладает "параллельный" перенос вектора по составным геодезическим на сфере. Вместе с тем, на рисунке рис.13 в цитируемой статье видно отчётливо: замкнутая траектория геодезической не является. Конечно, пространство, поверхность, на которой линия рис.2 является геодезической, в принципе, возможно. Однако в цитате такой вариант не отмечен. Следовательно, перенос не является ни параллельным, ни эквиугловым по отношению к какой-либо геодезической. Произвольный, не геодезический характер линии переноса не ведёт к повороту вектора при его эквиугловом переносе по замкнутой траектории. В исходную точку вектор возвращается без изменения направления. То, что вектор показан с изменившимся направлением после обхода траектории - это декларативное, бездоказательное решение.

Уточнение о геодезическом характере кривой, траектории переноса является важным обстоятельством. Принципиальная невозможность параллельного переноса вектора по сфере с неизбежностью требует замены параллельного переноса на эквиугловой. Такой перенос возможен как вдоль геодезической, прямой линии, так и вдоль произвольной линии. Но в последнем случае, если следовать буквально правилу транспортировки с сохранением угла, то вектор совпадёт со своим исходным направлением, поскольку в начальной-конечной точке существует единственное направление с заданным углом.

В двух последних приведённых выше цитатах нет явного указания на геодезический характер линий переноса, хотя, вероятно, он подразумевается. Отметим это обстоятельство как важное, решающее, но явно нигде не озвученное. Изменение направление вектора при его переносе происходит только в точках излома, точках перехода вектора с одной геодезической на другую. Если геодезическая замкнута и не имеет изломов, то вектор в исходную точку всегда возвращается без изменения направления.

Перенос вектора по поверхности конуса

Излом на геодезической может быть как в случае стыковки разных геодезических, так и вследствие её самопересечения. Такая ситуация может возникнуть, например, на поверхности конуса [57] при некоторых углах развертки образующей его плоскости. Заметим, что эти геодезические на конусе являются прямыми евклидовыми линиями. Косвенно на это обстоятельство обратил внимание Carroll, правда, в несколько ином ключе. Рассматривая криволинейную траекторию переноса вектора, он указал

"Конус - это пример двумерного многообразия с ненулевой кривизной ровно в одной точке. Мы можем увидеть это также, развернув его; конус эквивалентен плоскости с удаленным "дефицитным углом" и обозначенными противоположными сторонами" [3, с.83].

Рассматриваемый далее параллельный перенос в общих чертах в цитате описан верно: на поверхности конуса такой перенос возможен:

"В метрике, унаследованной от этого описания как часть плоской поверхности, конус плоский везде, кроме вершины. Это можно увидеть, рассматривая параллельную транспортировку вектора по различным петлям; если цикл не охватывает вершину, не будет общего преобразования, тогда как цикл, который действительно охватывает вершину (скажем, только один раз), приведет к повороту на угол, который является просто недостающим углом" [там же, с.84].

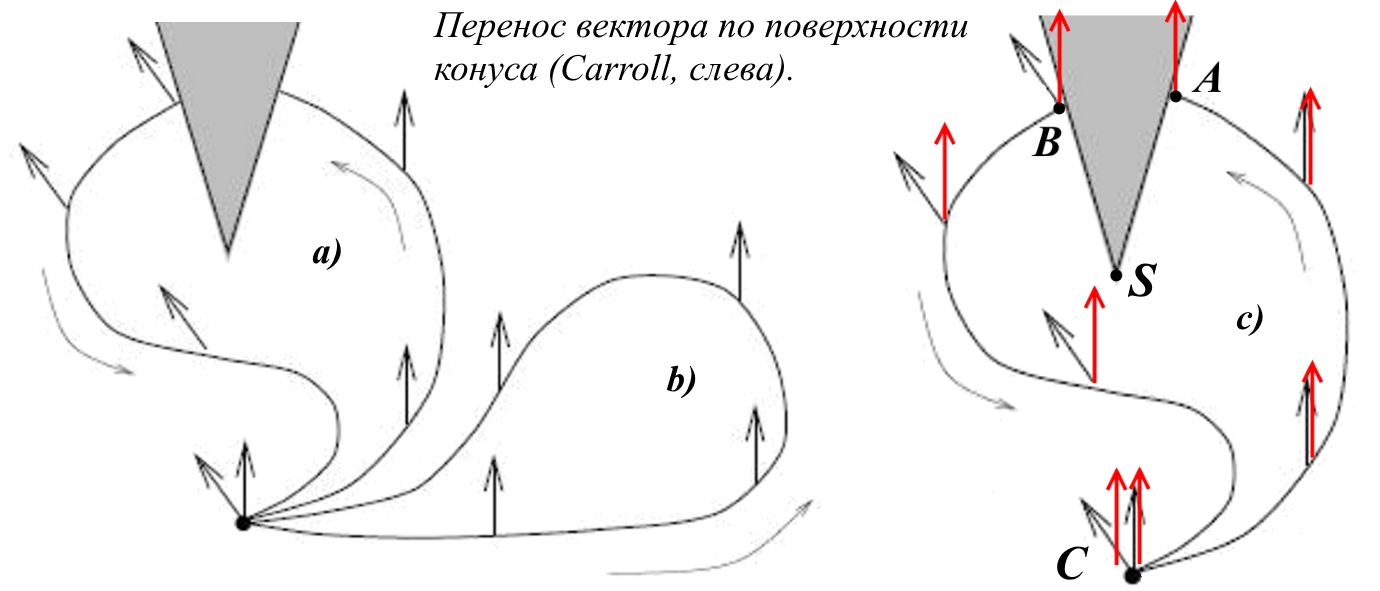
paraldox2

Рис.3. Перенос вектора по поверхности конуса [3, с.83]

Вместе с тем отметим, что на рисунках рис.3a и рис.3b просматривается странная ситуация. Действительно, вся поверхность конуса, приведённая на рисунке рис.3 в виде развёртки, является плоской в евклидовом смысле. Это прямо означает, что любые два отрезка, параллельные друг другу, остаются параллельными при любом параллельном переносе. Рассмотрим немного другую, инверсную ситуацию. Перенесём векторы A и B из конечной точки C независимо друг от друга, считая их изначально параллельными. В точках A и B эти векторы после переноса останутся параллельными. В чём тогда причина нарушения в цитате?

То, что, как указано в цитате, вектор после переноса по замкнутому контуру испытал поворот, прямо, классически означает: пространство конуса криволинейное. Либо следует признать, что параллельный перенос не может служить индикатором кривизны. Однако противоречие в ином.

Рассмотрим ещё один вариант переноса: в том же направлении перенесём вектор из точки B в точку A. Очевидно, что после такого переноса векторы будут строго параллельны, что соответствует их положению относительно линий координат. Однако визуально, из пространства погружения векторы будут расположены под углом, равным недостающему углу. Возникает естественный вопрос: так параллельны векторы или расположены под углом? Возникает также и второй вопрос-возражение: вектор B, вообще-то, строго говоря, не вернулся в исходную точку B, поскольку, как мы указали, путь завершён в точке A. Что будет, если перенести вектор через линию разреза? Линия разреза конуса - это линия, которую мы можем выбрать вдоль любой его образующей. На конусе эта линия разреза изначально не задана. Если мы обходим вершину конуса S полностью, по замкнутой кривой, то, естественно, мы рано или поздно будем вынуждены пересечь и линию разреза, скрывающую недостающий угол. Вот в чём и заключено это противоречие: вращение вектора происходит тогда и только тогда, когда он пересекает линию разреза. Не вершина конуса S является единственно не плоской точкрой, а линия разреза является запрещённой для пересечения линией. На поверхности конуса мы можем производить любые построения, которые будут строго соответствовать положениям евклидовой геометрии, но только с соблюдением запрета на пересечение линии разреза. Линию можно задать до нанесения координатной сетки на поверхность конуса, а можно и в процессе построений, если для неё останется пространство, в котором она не пересекает наши построения.

Для условных двухмерных обитателей поверхности конуса эта линия разреза имеет статус непреодолимой границы, своеобразной стены. Можно двигаться как угодно по поверхности, но пройти сквозь стену невозможно. Вернее, невозможно пройти без искажений. Эта стена является, так сказать, "кротовой норой" для обитателей поверхности конуса, своеобразной Чёрной дырой. Собственно говоря, эта ситуация возникает просто потому, что недостающий угол - это вырезанная часть плоскости Евклида. Участок плоскости, удалённый из неё. Никакие движения по несуществующему участку невозможны. Этот участок можно как угодно деформировать: сжать, растянуть, свернуть. Никакие манипуляции с ним не меняют этого участка: при любом изменении Ничего, если придавать этому изменению хоть какой-то смысл, Ничто остаётся Ничем.

Как вариант, стена может быть прозрачной. В этом случае любая линия, упёршаяся в стену, может быть продолжена обитателями за стеной. При этом как угодно: быть визуальным продолжением, либо также визуально лежать под таким же углом к линиям координат, как и повторяемая. Но это уже две разные линии. Следовательно, и линии CA и BC на рисунке рис.3с из цитаты не являются замкнутым контуром - это две разные линии. В цитате выбрано продолжение линии, BC, кажущееся "параллельным" линии CA. В кавычки мы взяли это слово, поскольку на самом деле точки A и B следовало бы считать одной точкой, точкой излома на линии, что формально означает - линии разные.

Как видим на сдвоенном рисунке рис.3a и рис.3b, перенос производится параллельно по произвольной траектории в разных областях конуса, по линии, не являющейся геодезической. Однако такой перенос в плоском пространстве не ведёт к повороту вектора. Если в результате такого переноса вектор изменил направление, то пространство не является плоским и в нём параллельный перенос невозможен, а допустим лишь эквиугловой перенос, причём только вдоль геодезической. То есть, в нашем случае невозможен и эквиугловой перенос, поскольку линии переноса не объявлены геодезическими, а визуально выглядят как линии произвольные. Эквиугловой перенос вектора вдоль произвольной линии не является индикатором искривлённости пространства, поскольку поворот вектора определить невозможно, он может быть любым.

Зададимся вопросом: как условный "плосковитянин", обитатель поверхности конуса, определяет, что линия переноса является геодезической, а перенос вектора - параллельным? Самым очевидным является использование координатной сетки. При её наличии все вопросы о геодезических и параллелях на плоскости снимаются.

В общем случае определение, выявление искривлённости поверхности без использования понятия погружения является неоправданно сложной процедурой, имеющей целый ряд недостатков и обязательных оговорок. Такой перенос целесообразно использовать лишь как демонстрацию, как геометрическое следствие одного из свойств искривлённого пространства, но никак не для его диагностики, тестирования. На рис.4 мы показали эквиугловой перенос вектора по плоскости по разным траекториям. Как видим, один и тот же вектор (слева) приходит в конечную точку (справа) с разным поворотом в зависимости от вида линии переноса. Две из них являются для плоскости геодезическим, по ним чёрный и зелёный векторы после перемещения сохранили свои направления. Но линии, содержащие негеодезические вставки, привели к повороту синего и красного векторов, причём в разные стороны. Отметим, что эквиугловой перенос по геодезическим на плоскости тождественен параллельному переносу.

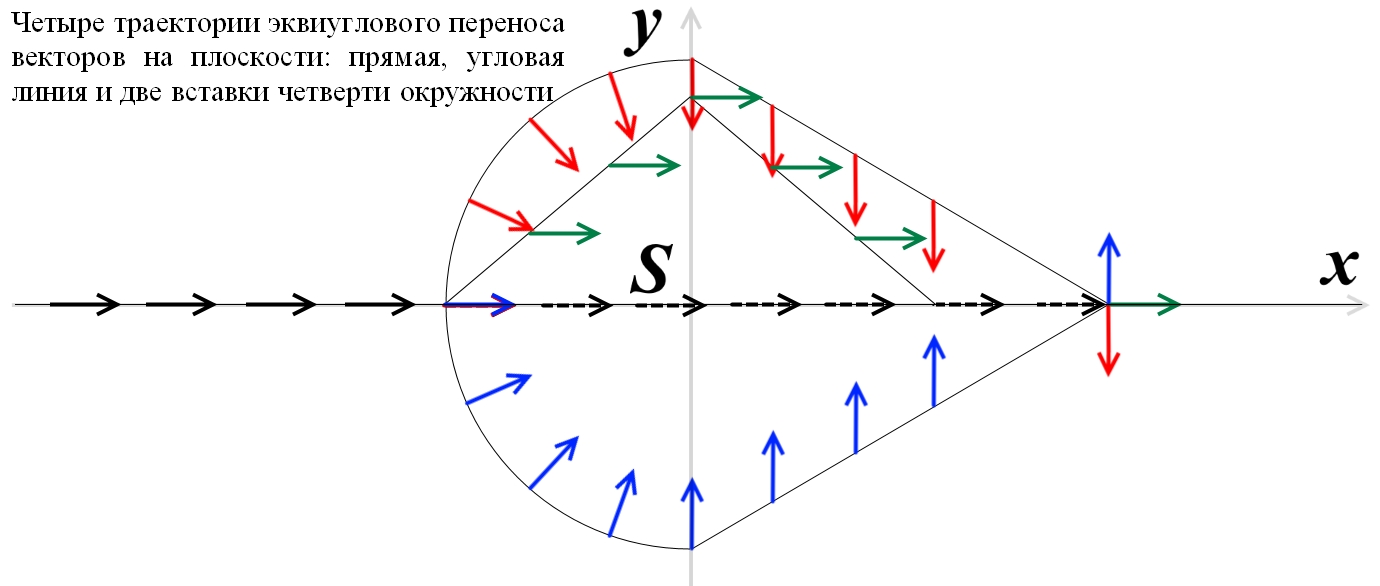
paraldox2

Рис.4. Четыре траектории эквиуглового переноса векторов на плоскости: прямая, угловая линия и две вставки четверти окружности

На рисунке рис.3a мы видим, что оригинальные векторы, обозначенные далее как A и B, не параллельны друг другу, то есть, пространство, поверхность определена, протествирована как искривлённая. В соответствии со свойством эквиуглового переноса вдоль линий, не являющихся геодезическими, если бы переносимый вектор имел неизменный угол к изображенной произвольной линии переноса, то в исходную точку он вернулся бы с любым наперёд заданным углом поворота. Однако перенос на рис.3a является ни параллельным, как заявлено, ни эквиугловым.

На рисунке рис.3c мы добавили красные векторы. Так на самом деле должен выглядеть параллельный перенос в плоском пространстве. Ещё раз отметим: важным моментом на рисунке является переход вектора через "недостающий угол". Две точки A и B на поверхности конуса - это точка, рассматриваемая в цитате как одна и та же, просто нами изображённая дважды. Вряд ли можно допустить, что в ней один и тот же вектор одновременно имеет разные направления, поэтому векторы A и B мы изобразили строго параллельными всем другим векторам, поддержав утверждение цитаты о параллельном переносе. Отметим ещё более определённо: развёртка конуса с "раскрытием" его "недостающего угла" явно демонстрирует, что эта поверхность является плоскостью. Тем не менее, при заявленном параллельном переносе, вектор принудительно повёрнут.

Если пренебречь запретом на переход через линию разреза, через недостающий угол, некоторые положения евклидовой геометрии на поверхности конуса будут нарушены. Например, прямая линия на конусе может пересекать саму себя. Две прямые линии, отрезки a и b на рис.5, могут образовывать геометрическую фигуру "двухугольник", то есть, они пересекаются дважды в двух разных точках - A и B.

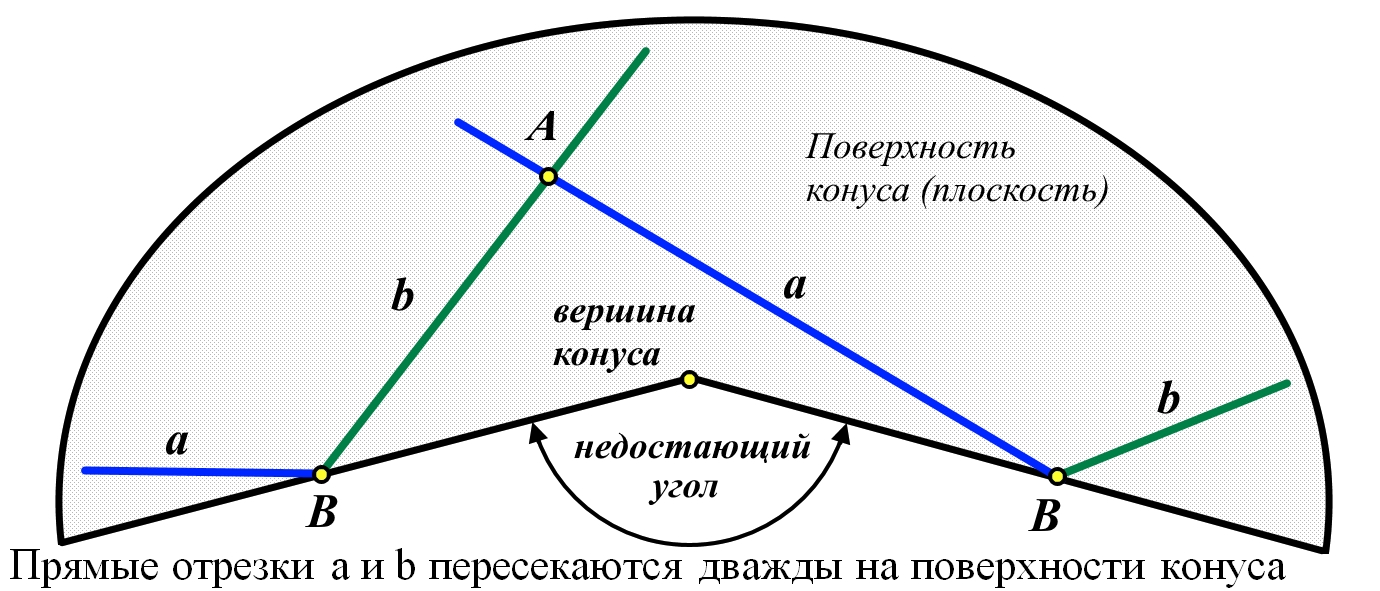
paraldox2

Рис.5. Прямые отрезки a и b пересекаются дважды на поверхности конуса

Помимо конуса с недостающим углом возможны конусы с избыточным углом [57]. На поверхности таких конусов можно наблюдать противоположный эффект: изначально параллельные линии, проходящие мимо полюса с двух сторон, начинают удаляться друг от друга.

Традиционно конус создают из плоскости, вырезав в ней угол из прямых линий - тот самый недостающий угол рис.6. Иначе говоря, часть плоскости буквально исчезает. Затем стороны угла смыкают, рис.7, вследствие чего и образуется коническая поверхность. Для наглядности и более удобного исследования конической поверхности угол следует вырезать относительно какой-либо из осей координат. На рис.6 мы вырезали угол в четвёртом квадранте, совместив одну из его сторон с осью абсцисс. На рис.7 мы сомкнули стороны угла и показали лишь участок поверхности вблизи линии смыкания, там где "спрятан" недостающий угол.

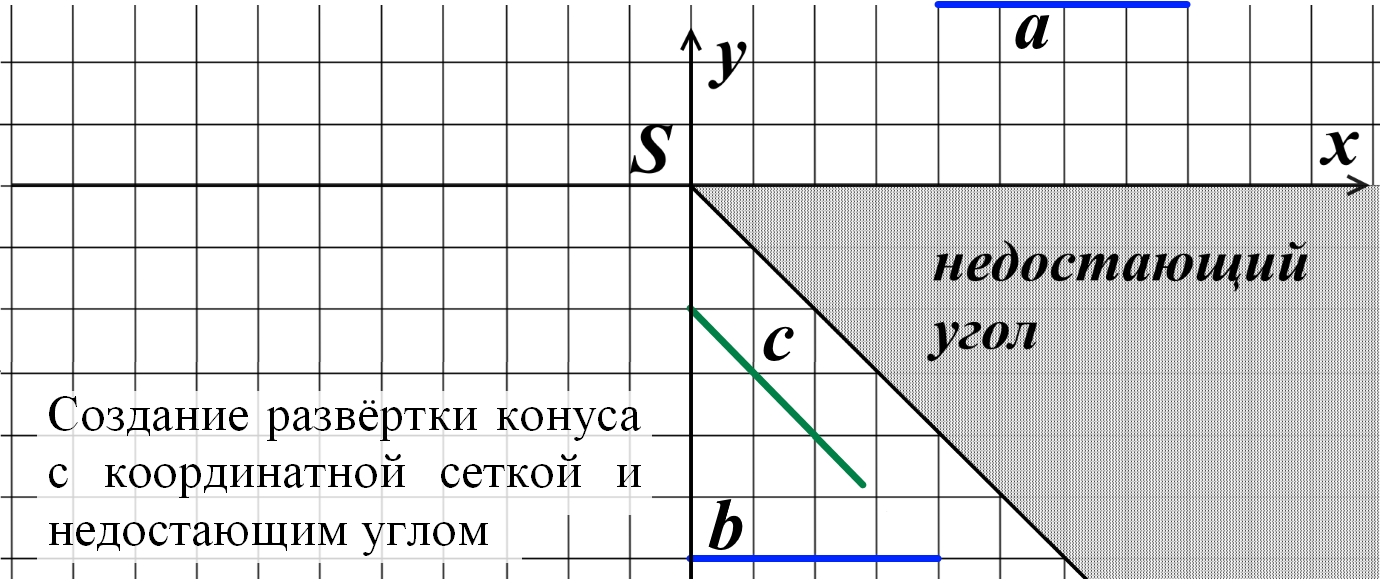
paraldox2

Рис.6. Создание развёртки конуса с координатной сеткой и недостающим углом

Сразу же заметим, что поверхность конуса при этом не имеет точек кривизны, вся она строго плоская в евклидовом смысле. Поскольку мы нанесли на его поверхность координатную сетку, сразу же можем отметить странную на первый взгляд ситуацию. На рис.6, на поверхности конуса параллельными являются отрезки a и b, хотя на рис.7 кажется, что они расположены под углом. Напротив, линии c и a параллельными не являются - рис.6, хотя извне явно видна их параллельность - рис.7. Это иллюзия: отрезки a и b расположены вдоль оси абсцисс и являются параллельными по определению. На развертке это видно отчётливо.

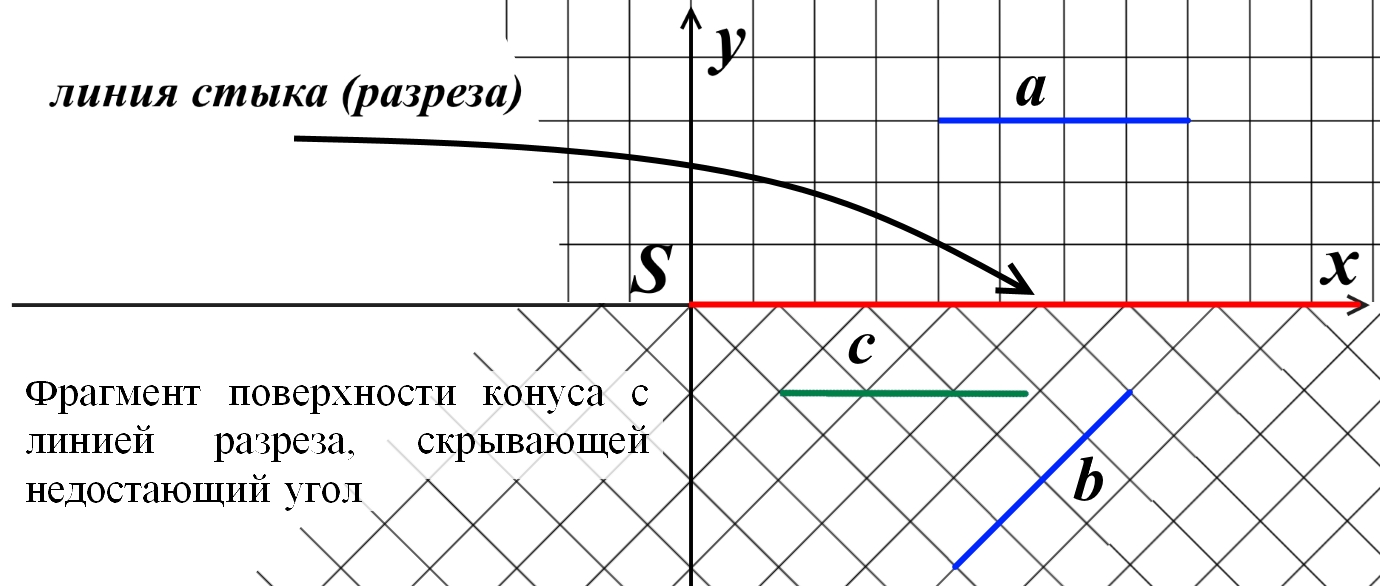
paraldox2

Рис.7. Фрагмент поверхности конуса с линией разреза, скрывающей недостающий угол

Отметим, что традиционный способ формирования конической поверхности вырезанием недостающего угла не является единственным. На следующем рисунке рис.8 изображена развёртка конической поверхности, образованной из плоскости с криволинейным недостающим углом. Аналитическое определение формы сторон такого произвольного угла, видимо, достаточно громоздки. Поэтому мы произведём обратную процедуру формирования этого угла. Обычным способом создаём конус из плоскости с нанесённой координатной сеткой и вырезанным недостающим углом, как показано на рис.6. Далее на поверхности конуса мы рисуем произвольную линию, наугад. После этого ножницами разрезаем поверхность конуса вдоль этой линии и, как результат, получаем плоскую развертку рис.8. Поскольку поверхность конуса мы объявили строго евклидовой плоскостью, то исходную координатную сетку с вырезом рис.6 мы заменяем на сетку первого квадранта, просто расширив её на всю поверхность развёртки кроме вырезанных областей. Эти области недостающих углов являются областями, запретными для построений и даже для их пересечения. Границы углов при построениях означают буквально физические границы, как границы обычного чертёжного листа. Вопросы параллельности и параллельного переноса векторов решаются строго в рамках евклидовой плоскости с учётом "дырок" на листе.

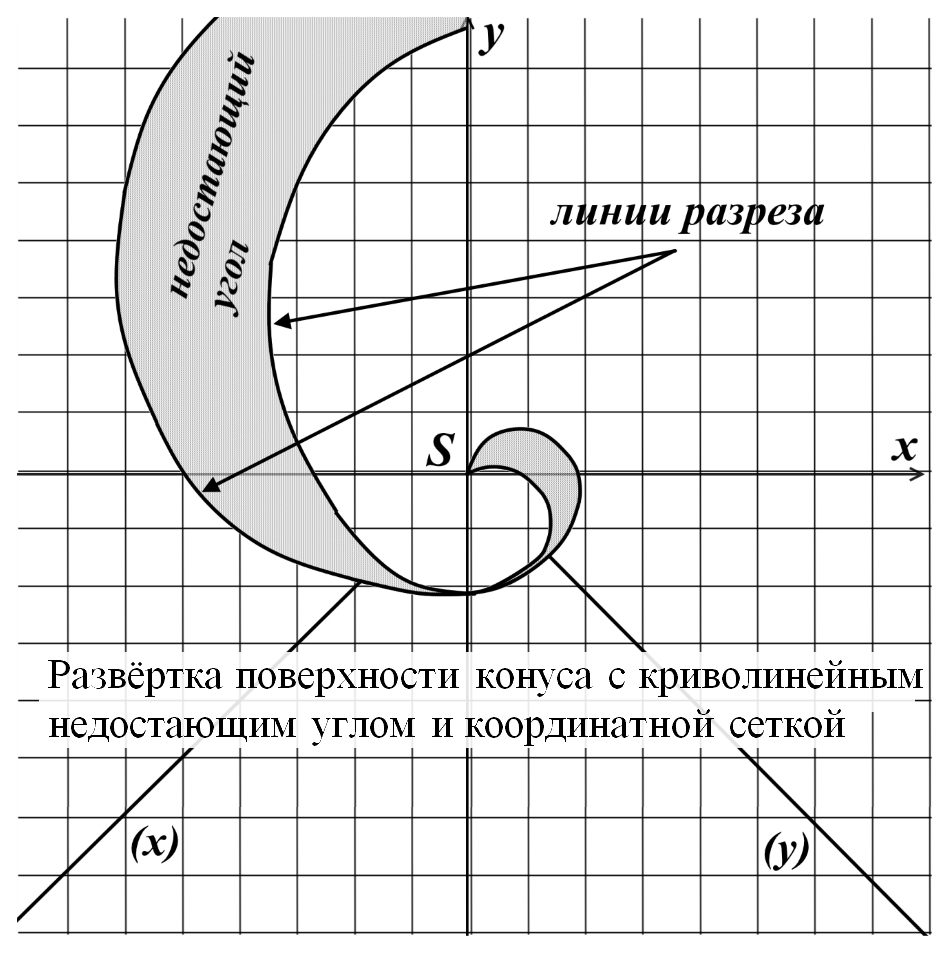
paraldox2

Рис.8. Развёртка поверхности конуса с криволинейным недостающим углом и координатной сеткой

Очевидно, что любая линия, пересекающая нарисованную нами линию разреза, линия, кажущаяся сплошной на поверхности конуса, на самом деле является составной: до разреза и после него. В области линии разреза, в точке касания разреза, эта составная линии лишь кажется сплошной и без излома. На развёртке в этой точке линия, казавшаяся сплошной, разбивается на две независимые, не соприкасающиеся линии. Если эта линия была на конусе визуально прямой линией, то на развёртке эти два фрагмента находятся под углом, равным недостающему углу исходного конуса рис.6. Заметим, что такой поворот напоминает прохождение луча света через призму.

Таким же двусмысленным свойством быть плоскостью и одновременно искривлённой поверхностью обладает поверхность куба - рис.9. Если по его поверхности вектор переносится по замкнутому контуру произвольной формы, параллельно и без обхода, охвата какой-либо из его вершин, то в исходную точку вектор возвращается без поворота - рис.9b. Если же контур охватывает какую-либо вершину, то даже при строго параллельном переносе по геодезической вектор возвращается в исходную точку с поворотом. Угол поворота всегда кратен прямому. Например, при охвате двух вершин куба вектор меняет своё направление на противоположное, при охвате одной вершины - поворот равен 90 градусам, рис.9а.

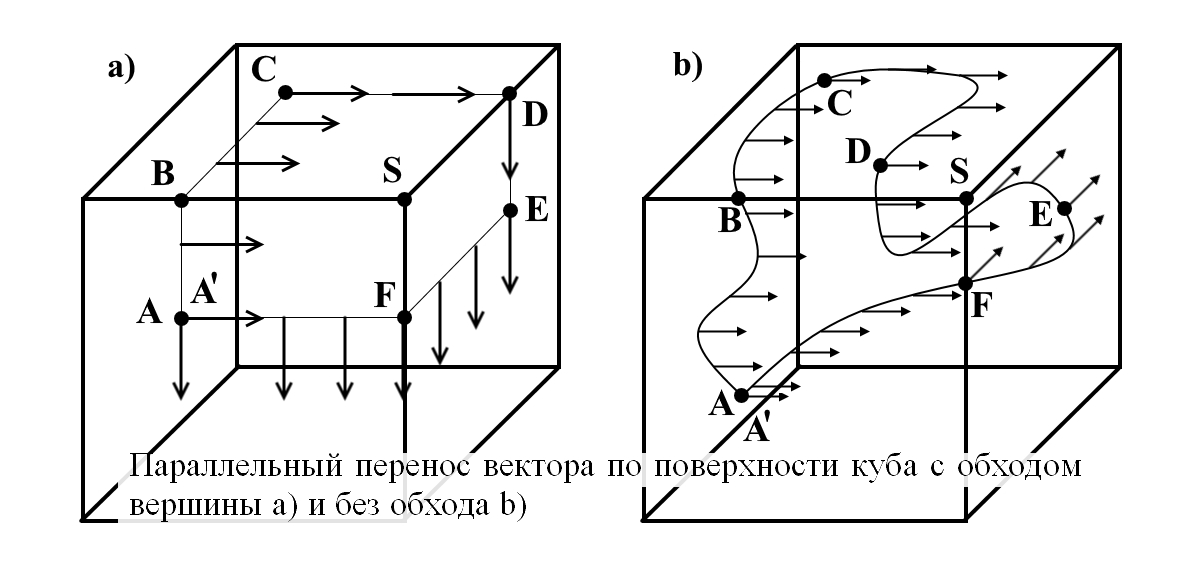
paraldox2

Рис.9. Параллельный перенос вектора по поверхности куба с обходом вершины a) и без обхода b)

Такое сходство вполне объяснимо. Три смежные грани куба эквивалентны поверхности некоего конуса, который просто "разглажен" с образованием трёх рёбер. Кстати, граней может быть сколько угодно, то есть, конус можно деформировать, превратив в многогранную пирамиду. Более того, можно заметить сходство сдвоенного конуса помимо куба с другими фигурами: сферой и октаэдром - рис.10. Сходство этих фигур можно заметить в плане наличия полюсов, как на сфере. Каждая из фигур рис.10 имеет три пары полюсов. Мы расположили фигуры так, чтобы их верхнюю и нижнюю точки обозначить как полюса север и юг. Остальные полюса удобно рассмотреть сначала на примере сферы. Традиционно в качестве системы координат сферы используются меридианы и параллели. Однако это не единственный вариант. Координаты могут быть образованы и ортогональными параллелями и ортогональными меридианами, как показано на рис.10b. Две системы меридиан означают наличие двух пар полюсов. Традиционная пара, как показано на рисунке, это север и юг. Вторую пару полюсов, для второго набора меридиан мы назвали Запад-Восток. Отметим интересную деталь. Если мы находимся на полюсе, то у нас существует единственное направление - на смежный полюс. В случае двух систем меридианов, двух пар полюсов таких направление становится больше. Находясь, например, на северном полюсе, во всех направлениях у нас будет юг. Но не только. Появляется ещё два направления: это юго-восток и юго-запад. Причём возникшие ещё два направления выглядят двусмысленно: это направление точно между западом и востоком. Эта двусмысленность позволила ввести ещё одну пару полюсов, которую мы называли Полдень и Полночь. То есть, находясь на северном полюсе, мы имеем ещё два направления: юго-полдень и юго-полночь. Эти два дополнительных полюса не нужны для создания координатной сетки, поскольку два набора меридианов и две пары полюсов однозначно определяют координаты любой точки на поверхности сферы.

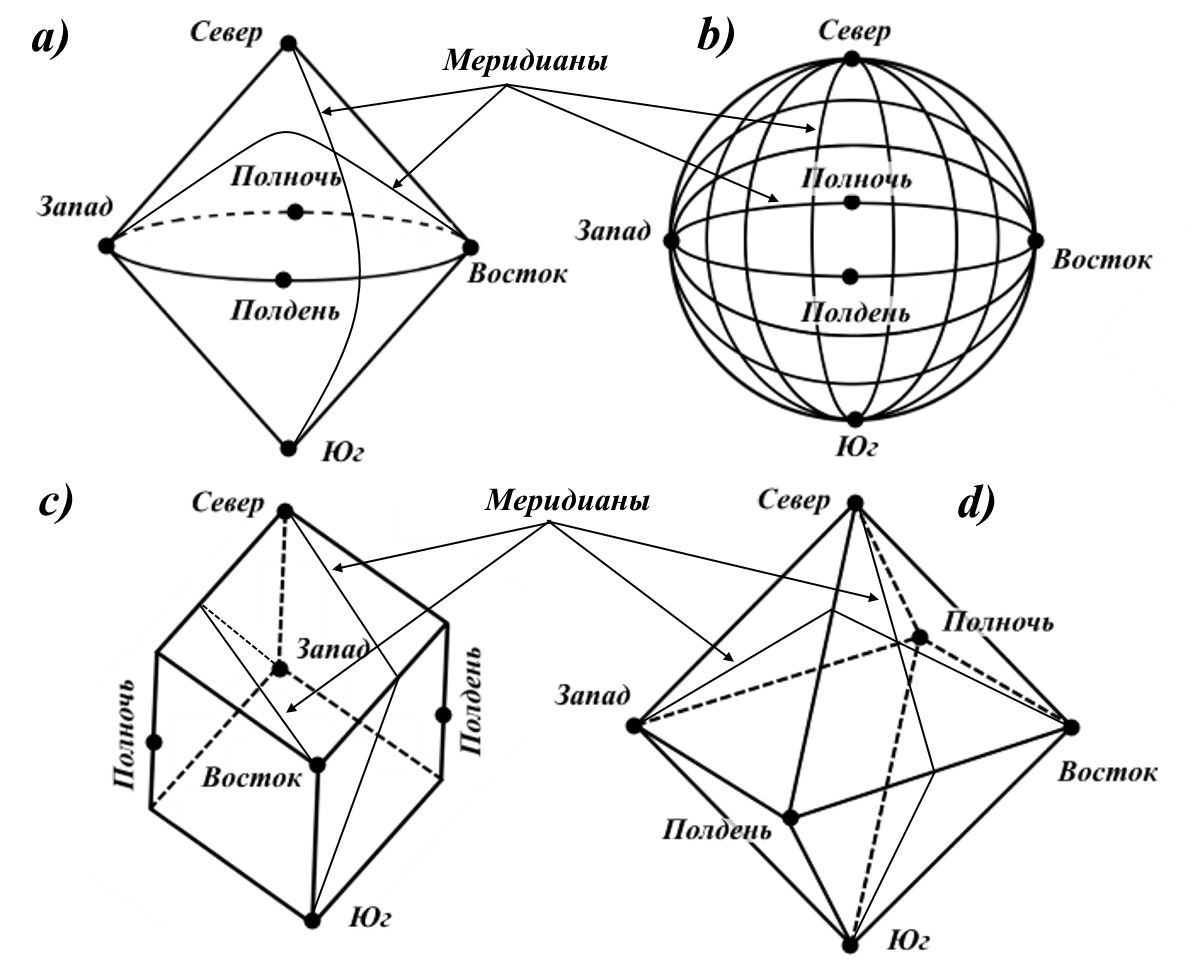
paraldox2

Рис.10. Меридианные координаты на сдвоенном конусе, сфере, кубе и октаэдре.

По аналогии со сферой мы можем установить такие же три пары полюсов на сдвоенном конусе и на октаэдре - рис.10a,d. Отметим некоторое отличие полюсов на кубе. Две пары - юг-север и запад-восток - ничем не отличаются от таковых на других фигурах. Но пара полюсов Полдень-Полночь иная. Мы можем обозначить их двояко: либо как точки на серединах боковых рёбер куба, либо как сами эти рёбра. По сути, это не принципиально и не имеет никаких противоречий.

На каждой из фигур в качестве примера мы изобразили по одному ортогональному меридиану. Для каждой пары меридианных полюсов смежные нулевые меридианы являются экваторами.

Заключение

На искривлённых поверхностях не существует параллельных линий и, следовательно, никакой перенос вектора не может быть параллельным. Из этого прямо следует: параллельный перенос вектора в рамках пространства не может служить индикатором кривизны пространства, в частности, на поверхности сферы. Подобное несоответствие возникает и на поверхности Лобачевского. Это справедливо в отношении любой искривленной поверхности.

Любой перенос вектора, лежащего в плоскости, касательной к искривлённой поверхности, может свидетельствовать только об искривлении пространства погружения, то есть, пространства, в котором находятся как искривлённая поверхность, так и касательная плоскость с вектором. Параллельный перенос касательного вектора в E³ пространстве погружения Евклида всегда сохраняет его направление. Такой касательный вектор не принадлежит искривлённому пространству и имеет с ним только одну общую точку - начало вектора.

Исследование кривизны пространства возможно с использованием эквиуглового перемещения вектора, то есть, его перемещения с сохранением угла относительно линии переноса. Линией переноса обязательно должна быть геодезическая. Если эта линия замкнута и не имеет излома, то вектор вернётся в исходную точку без поворота и точно совпадёт со своим исходным направлением. Если геодезическая переноса имеет излом, то вектор изменит своё направление на величину угла в точке излома геодезической.

Использование для переноса вектора произвольной, не геодезической линии, в том числе, путём аппроксимации произвольной линии бесконечно малыми отрезками геодезических, приводит к невозможности визуализации как параллельного, так и эквиуглового переноса.

Перенос вектора по произвольной замкнутой траектории или по разным путям с сохранением угла к линии переноса может привести к изменению его направления в любом пространстве, в том числе на плоскости Евклида.

На поверхности конуса геодезическая - евклидова прямая линия - может пересекать саму себя, то есть, быть замкнутой прямой линией с изломом. Перенос вектора по замкнутому контуру на такой плоской поверхности приведёт к его повороту.

В качестве линии разреза конуса для формирование его развёртки может использоваться как его образующая, так и любая, произвольная линия.

Литература

1. Blau M. Lecture notes on General Relativity \\ Albert Einstein Center for Fundamental Physics Institut fur Theoretische Physik Universitat Bern, CH-3012 Bern, Switzerland, 2017, URL: http://www.blau.itp.unibe.ch/Lecturenotes.html

2. Carroll S. Spacetime and geometry. An Introduction to General Relativity. University of Chicago, Copyright No 2004 Pearson Education, Inc., publishing as Addison Wesley, ISBN 0-8053-8732-3 (hardcover)

3. Carroll S.M. Lecture Notes on General Relativity, arXiv:gr-qc/9712019v1 3 Dec 1997

4. Ekhammar S., Erkensten D., Lassila M., Nilsson T. From Black Holes to Wormholes in Higher Spin Gravity. 2+1-dimensional gravity in a Chern-Simons formulation. Department of Physics, Chalmers University of Technology, Gothenburg, Sweden 2017

5. Gerard 't Hooft Introduction to General Relativity. Institute for Theoretical Physics, Utrecht University and Spinoza Institute, the Netherlands, 2012, URL: https://webspace.science.uu.nl/~hooft101/lectures/genrel_2010.pdf

6. Hendry M. An Introduction to General Relativity, Gravitational Waves and Detection Principles. University of Glasgow, UK, 2007

7. Marolf D. Notes on Relativity and Cosmology. Physics Department, Syracuse University, 2003, URL: https://ru.scribd.com/document/38274054/Relativity-and-Cosmology-Notes

8. Ryder L. Introduction to General Relativity. University of Kent, UK. Cambridge University Press, New York, 2009

9. Schutz B.F. A First Course in General Relativity. Second Edition. Max Planck Institute for Gravitational Physics. Cambridge University Press, New York, 2009

10. Straumann N. General relativity : with applications to astrophysics / Norbert. - Berlin [etc.]: Springer, cop. 2004. - xii, 674 с. : ил., портр.; 25 см

11. Wald R.M. General relativity. The University of Chicago Press, Chicago and London, 1984. URL: https://www.pdfdrive.com/general-relativity-r-waldpdf-e19758319.html

12. Александров П.С. Что такое неэвклидова геометрия. - М.: Изд. академии пед. наук РСФСР, 1950.

13. Беллони Л., Рейна Ч. Прецессия Томаса. Подход Зоммерфельда. В сборнике: Эйнштейновский сборник, 1984 - 1985: Сб. статей. - М.: Наука, 1988.

14. Бергман П. Загадка гравитации \\Перевод с английского В.А.Угарова. - М.: Наука. Гл. ред. физ.-мат. лит., 1969

15. Бергман П.Г. Введение в теорию относительности, с предисловием А. Эйнштейна \\Пер. с анг. П. Кунина и И. Таксара, под редакцией Б. Л. Гинзбурга. - М.: Гос. изд. иностранной литературы, 1947

16. Бескин В.С. Гравитация и астрофизика. - М.: Физический институт им. П.Н.Лебедева РАН. Учебно-Научный Комплекс, 2007

17. Бим Дж., Эрлих П. Глобальная лоренцева геометрия, - М.: Мир, 1985. - 400 с.

18. Богородский А.Ф. Уравнения поля Эйнштейна и их применение в астрономии. Изд-во Киевского университета, 1962 г.

19. Введение в общую теорию относительности, ее современное развитие и приложения : [учеб. пособие] / С. О. Алексеев, Е. А. Памятных, А. В. Урсулов, Д. А. Третьякова, К. А. Ранну; М-во образования и науки Рос. Федерации, Урал. федер. ун-т. - Екатеринбург : Изд-во Урал. ун-та, 2015. - 380 с. ISBN 978-5-7996-1584-0

20. Вебер Дж. Общая теория относительности и гравитационные волны. \\ Пер. с анг. Н. Мицкевича. Под редакцией проф. Д.. - М.: Изд. иностранной литературы, 1962.

21. Вейль Г. Пространство. Время. Материя. Лекции по общей теории относительности: Пер. с нем. Изд. 2-е, испр. - М.: Едиториал УРСС, 2004. - 456 с.

22. Вергелес С.Н. Лекции по теории гравитации. Учебное пособие. - М., МФТИ, 2001.- 428с.

23. Владимиров Ю.С. Классическая теория гравитации: Учебное пособие. -- М.: Книжный дом "ЛИБРОКОМ", 2009, 264 с.

24. Гильберт Д. "Основания геометрии", пер. с 7-го немецкого издания И.С.Градштейна, Москва - Ленинград, ОГИЗ, Гос. изд. тех.-теор. лит-ры, 1948 г.

25. Горбунов Д.С., Рубаков В.А. Введение в теорию ранней Вселенной: Теория горячего Большого взрыва. - М.: Издательство ЛКИ, 2008. - 552 с., цв. вкл.

26. Гравитация и относительность. Под редакцией X. Цзю и В. Гоффмана. Пер. с анг. Д.В.Белова и И.В.Мицкевича под редакцией А.3.Петрова. - М.: Изд. "Мир", 1965 г.

27. Гуревич Л.Э., Чернин А.Д. Общая теория относительности в физической картине мира. Гравитация, космология, космогония, М.- "Знание", 1970, 62 стр.

28. Евклид "Начала", книги I-VI, пер. с греч. и комментарии Д.Д.Мордухай-Болтовского, ОГИЗ, Гос. изд. тех.-теор. лит-ры, Москва - Ленинград, 1950 г.

29. Зельдович Я.Б., Блинников С.И., Шакура Н.И. Физические основы строения и эволюции звезд, МГУ, 1981

30. Зельманов А.Л., Агаков В.Г. Элементы общей теории относительности. - М.: Наука. Гл. ред. физ.-мат. лит., 1989.

31. Иваненко Д.Д, Сарданашвили Г.А. Гравитация / Отв. ред. П.И.Фомин. Изд. 5-е. - М.: Издательство ЛКИ, 2012, 200с.

32. Катанаев М.О. Лекции по общей теории относительности. Математический институт имени В. А. Стеклова Российской Академии Наук, 2018 г. URL: http://www.mathnet.ru/supplement/conf/1354/lecture10.pdf

33. Кауфман Уильям Дж. Космические рубежи теории относительности. М.: "Мир", 1981, 352 с.

34. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: Учеб. пособ.: Для вузов. В 10 т. Т. П. Теория поля. - 8-е изд., стереот. - М.: ФИЗМАТЛИТ, 2003. - 536 с. - (Т. II).
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: Учеб. пособие. В 10 т. Т. П. Теория поля.-- 7-е изд., испр.-- М.: Наука. Гл. ред. физ.-мат. лит., 1988. 512 с. -- ISBN 5-02-014420-7 (Т. II).

35. Мёллер К. Теория относительности. Изд. 2-е. Пер. с англ. Под ред. проф. Д.. М., Атомиздат, 1975, 400 с.

36. Мизнер Ч., Торн К., Уилер Дж. Гравитация, т.1-3. - М.: "Мир", 1977

37. Никулин В.В., Шафаревич И.Р. Геометрии и группы. - М.: Наука, 1983, - 240 с.

38. Парадоксы параллельности, Самиздат, URL: http://samlib.ru/editors/p/putenihin_p_w/paraldox.shtml

39. Парадоксы параллельности. Часть 1, Самиздат, URL: http://samlib.ru/editors/p/putenihin_p_w/paraldox1.shtml

40. Парадоксы параллельности. Часть 2, Самиздат, URL: http://samlib.ru/editors/p/putenihin_p_w/paraldox2.shtml

41. Параллельные прямые, Википедия, URL: https://ru.wikipedia.org/wiki/Параллельные_прямые

42. Параллельные прямые, Математический справочник, URL: http://dict.scask.ru/index.php?id=1177

43. Паули В. Теория относительности: Пер. с нем. и англ. - 3-е изд., испр./Под род. В. Л. Гинзбурга и В. П. Фролова,-- М.: Наука. Гл. ред. физ.-мат. лит., 1991. (Б-ка тсор. физики). - 328 с - ISBN 5-02-014346-4.

44. Пенроуз Р. Новый ум короля: О компьютерах, мышлении и законах физики: Пер. с англ. / Общ. ред. В.О.Малышенко. - М.: Едиториал УРСС, 2003. - 384 с.

45. Пенроуз Р. Путь к реальности или законы, управляющие Вселенной. Полный путеводитель. \\ Пер. с анг. А.Р.Логунова и Э.М.Эпштейна, R&C, Москва, Ижевск, 2007

46. Петров А.Н. Гравитация. От хрустальных сфер до кротовых нор. Фрязино: "Век 2", 2013. - 320 с.

47. Путенихин П.В. Логические основания многомерных пространств. -- Саратов: "АМИРИТ", 2018. - 396 с., цв. илл., ISBN 978-5-907035-29-4, URL: https://www.twirpx.org/file/3089642/
https://www.elibrary.ru/item.asp?id=42690781

48. Рашевский П.К. Курс дифференциальной геометрии. - М.-Л., ГИТТЛ, 1950

49. Рашевский П.К. Риманова геометрия и тензорный анализ. Изд.3. - М., "Наука", 1967. - 664 с., ил.

50. Сажин М.В. Теория относительности для астрономов. ГАИШ, Москва

51. Синг Дж.Л. Общая теория относительности. \\ Пер. с анг. Б.Т.Вавилова. Под редакцией А.3.Петрова. - М.: Изд. иностранной литературы, 1963.

52. Тайсон Н.Д., Стросс М.А., Готт Д.Р. Большое космическое путешествие. Пер. на рус. ООО Издательство "Питер", 2018

53. Тейлор Э.Ф., Уилер Дж.А. Физика пространств времени, пер. с анг. Н. В. Мицкевича. Изд. второе, доп. - М.: Мир, 1971, - 320 с.

54. Торн К.С. Черные дыры и складки времени: Дерзкое наследие Эйнштейна. Перевод с англ. под ред. чл.-корр. РАН В.Б. Брагинского. - М.: Изд. физ.-мат. лит-ры, 2007, 616 с.

55. Трёхмерное эллиптическое пространство положительной кривизны. Диск и шар Римана, Самиздат, URL: http://samlib.ru/editors/p/putenihin_p_w/spheriman.shtml

56. Фейнман Р.Ф., Мориниго Ф.Б., Вагнер У.Г. Фейнмановские лекции по гравитации. \\ Под редакцией Б.Хатфилда. Введение Дж.Прескилла и К.С.Торна. Пер. с анг. д.ф.-м.н. А.Ф.Захарова, Москва, "Янус-К", 2000

57. Феномен конуса, Самиздат, URL: http://samlib.ru/p/putenihin_p_w/cone.shtml

58. Фридман А.А. Мир как пространство и время. Изд. второе. - М.: Изд. "Наука", 1965 г.

05.01 - 23.01.2022

Оставить комментарий © Copyright Путенихин Петр Васильевич (pe_put@rambler.ru) Размещен: 23/01/2022, изменен: 23/01/2022. 53k. Статистика. Статья: Естествознание Геометрия Иллюстрации/приложения: 10 шт. Скачать FB2		Ваша оценка:
Аннотация: На искривлённых поверхностях не существует параллельных линий, следовательно, никакой перенос вектора не может быть параллельным. Под параллельным переносом вектора подразумевается эквиугловой перенос, то есть, перенос с сохранение угла между вектором и линией переноса. Такой условный параллельный перенос вектора не может служить индикатором кривизны пространства, в частности, на поверхности сферы. Перенос вектора по произвольной замкнутой траектории или по разным путям с сохранением угла к линии переноса может привести к изменению его направления в любом пространстве, в том числе на плоскости Евклида. There are no parallel lines on curved surfaces, so no vector transfer can be parallel. Parallel transfer of a vector means equiangular transfer, that is, transfer with preservation of the angle between the vector and the transfer line. Such a conditional parallel transfer of a vector cannot serve as an indicator of the curvature of space, in particular, on the surface of a sphere. Transferring a vector along an arbitrary closed trajectory or along different paths while maintaining the angle to the transfer line can lead to a change in its direction in any space, including the Euclidean plane.

Путенихин Петр Васильевич : другие произведения.

Парадоксы параллельности. Часть 2