Парадокс близнецов - обзор решений,
гл.4 Решение парадокса близнецов в ОТО
Путенихин П.В.
4. Решение парадокса близнецов в ОТО
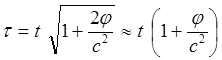 (9.15)
(9.15)
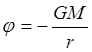
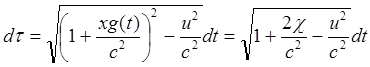 (4.1)
(4.1)
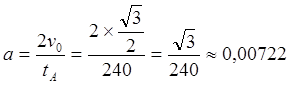
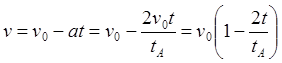
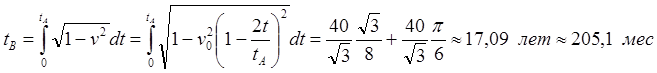
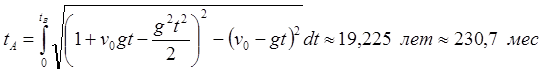
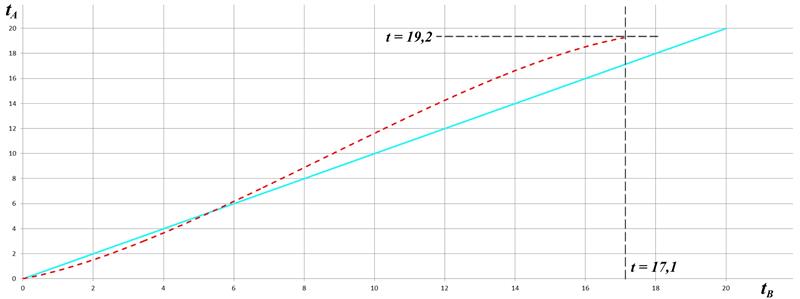
Рис.4.1 Численное интегрирование уравнения (4.1)
![]() (4.2)
(4.2)
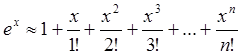
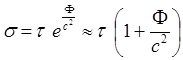
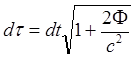 (4.26)
(4.26)
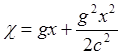 (4.3)
(4.3)
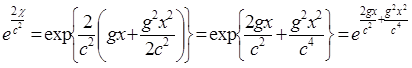
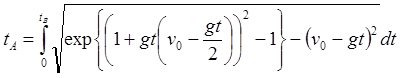 (4.4)
(4.4)
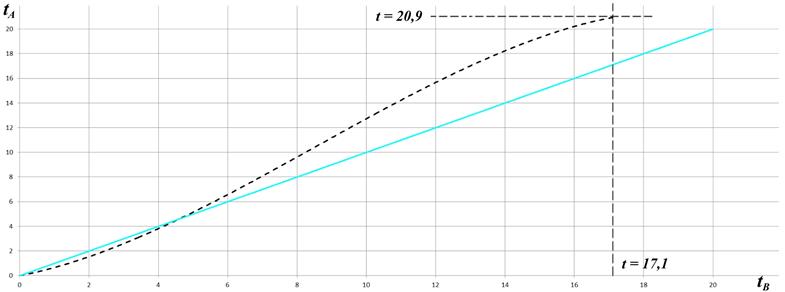
Рис.4.2 Численное интегрирование уравнения (4.4)
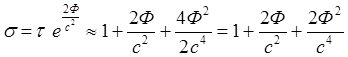
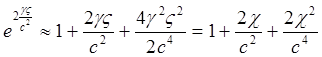
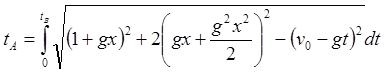 , (4.5)
, (4.5)
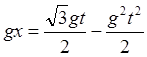 (4.6)
(4.6)
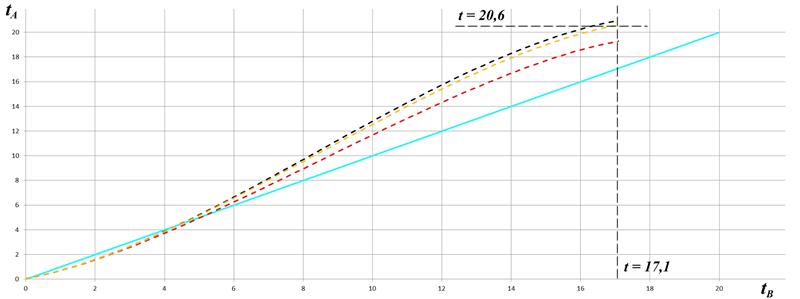
Рис.4.3 Численное интегрирование уравнения (4.5)
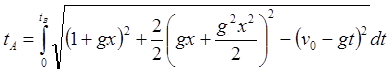 (4.7)
(4.7)
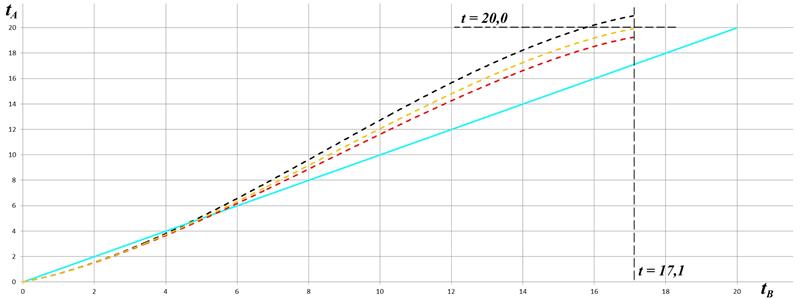
Рис.4.4 Численное интегрирование уравнения (4.7)
![]()
![]()
![]()
![]()
![]() (4.8)
(4.8)
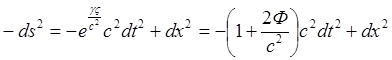
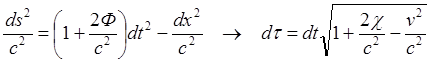
![]()
![]() (18.1)
(18.1)
![]()
![]() (7.2)
(7.2)
![]()
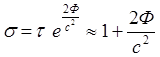
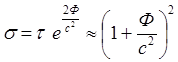
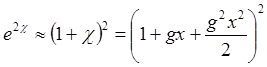
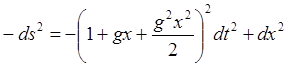
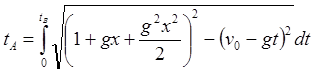 (4.9)
(4.9)
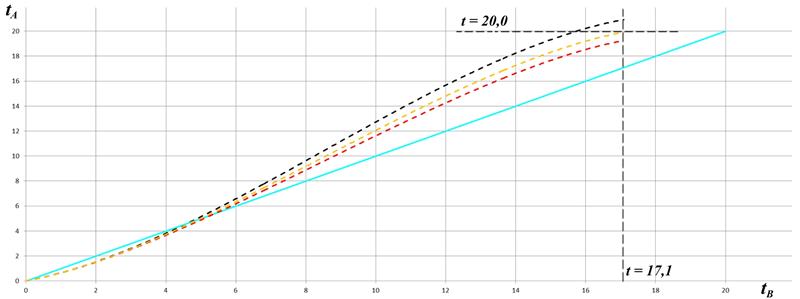
Рис.4.5 Численное интегрирование уравнения (4.9)
11. Приложения
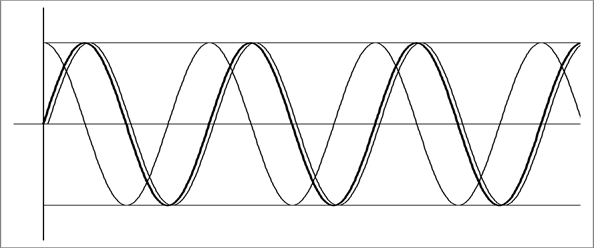
Рис.11.1 Числовой интеграл функции cos(x)
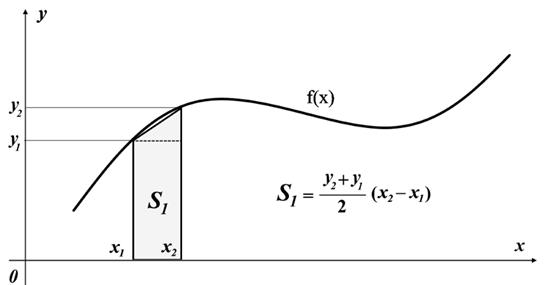
Рис.11.2 Площадь интегральной трапеции
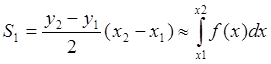
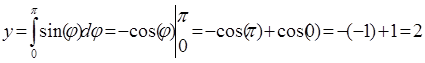
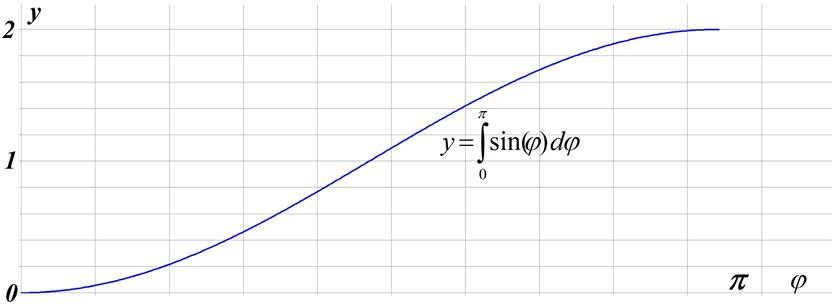
Рис.11.3 Численное интегрирование уравнения Sin(x)
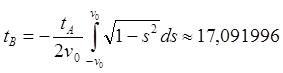 (11.1)
(11.1)
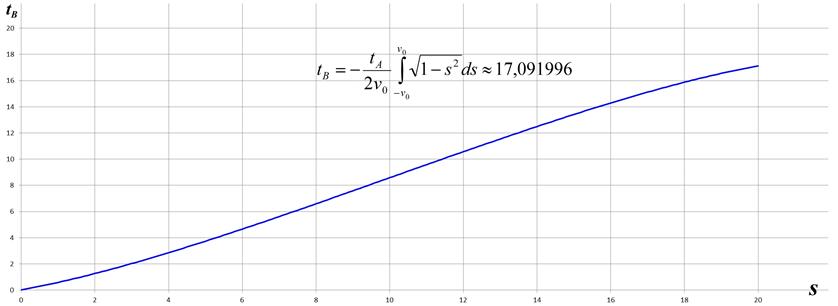
Рис.11.4 Численное интегрирование уравнения (11.1)
Литература