Парадокс близнецов - обзор решений,
гл.8 Обзор ОТО-решений парадокса
Путенихин П.В.
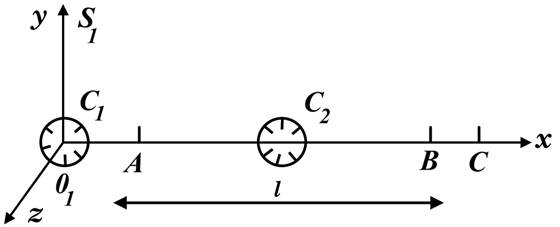
Рис.8.1 Иллюстрация к решению Мёллера [5, с.230]
![]()
![]()
![]()
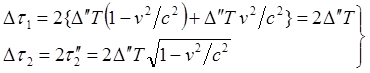
![]()
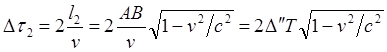
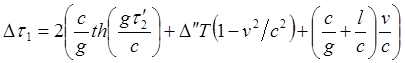
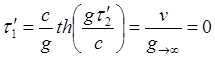
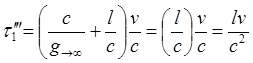
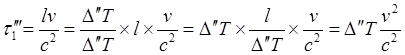
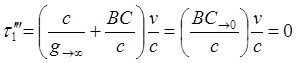
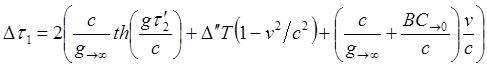
![]()
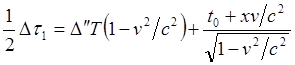
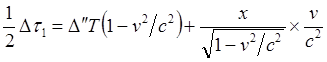
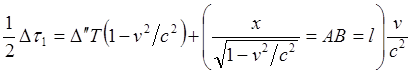
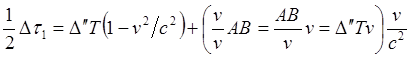
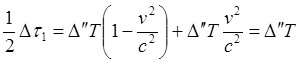
![]()
![]()
![]()
![]()
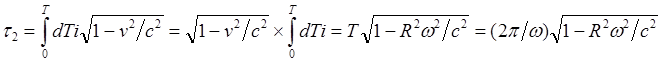 (8.3.1)
(8.3.1)
![]()
![]()
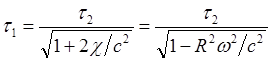
(8.3.2)
![]()
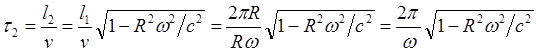
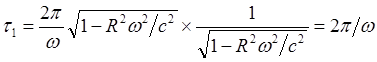 (8.3.3)
(8.3.3)
![]() (8.109)"
(8.109)"
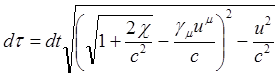 (8.114)
(8.114)
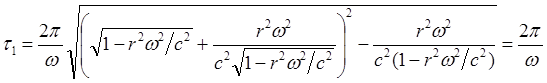 (8.201)
(8.201)
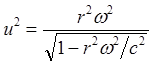
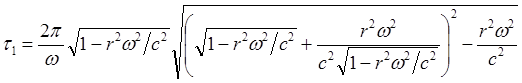 (8.3.4)
(8.3.4)
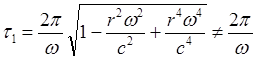
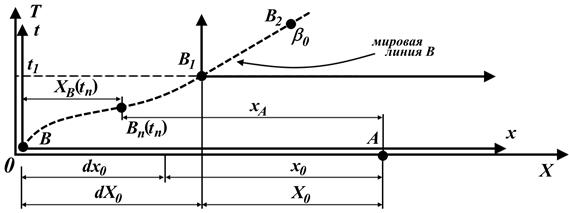
Рис.8.2 Иллюстрация к решению Скобельцына [7, с.100]
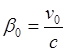
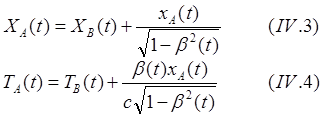
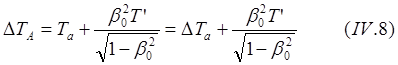
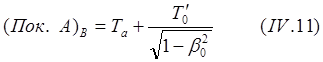
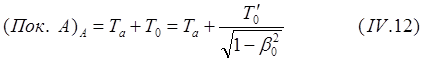
![]()
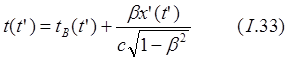
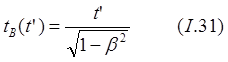
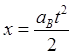
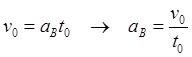 (8.4.01)
(8.4.01)
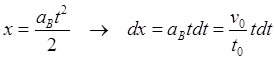
![]()
![]() (8.4.02)
(8.4.02)
![]() (8.4.03)
(8.4.03)
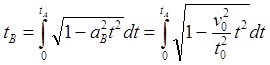 (8.4.04)
(8.4.04)
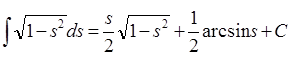
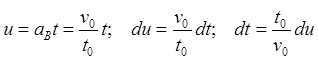
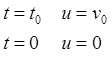
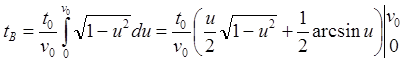
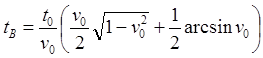 (8.4.05)
(8.4.05)
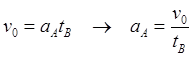 (8.4.06)
(8.4.06)
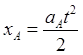
![]()
![]() (8.4.07)
(8.4.07)
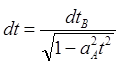 (8.4.08)
(8.4.08)
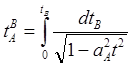 (8.4.09)
(8.4.09)
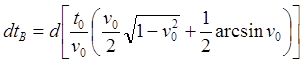
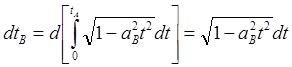 (8.4.10)
(8.4.10)
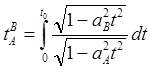 (8.4.11)
(8.4.11)
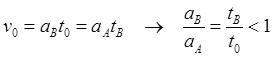 (8.4.12)
(8.4.12)
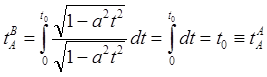
![]()
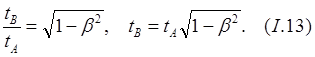
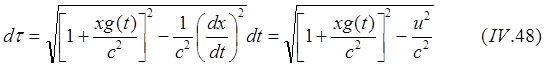
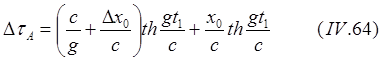
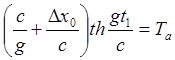
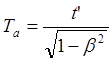
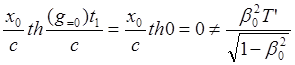
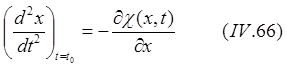
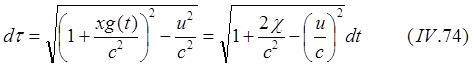
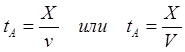
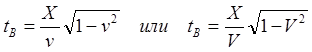 (8.5.1)
(8.5.1)
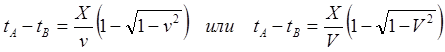
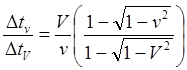 (8.5.2)
(8.5.2)
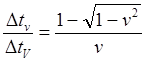 (8.5.3)
(8.5.3)
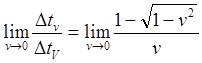
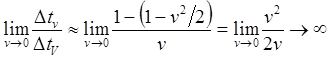 (8.5.4)
(8.5.4)
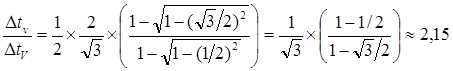
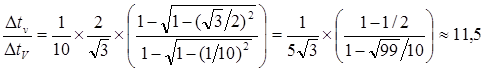
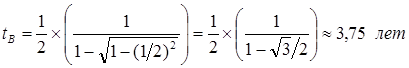
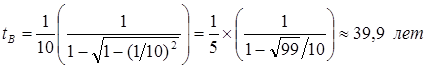
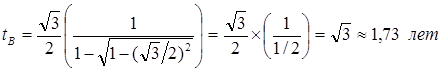
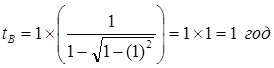
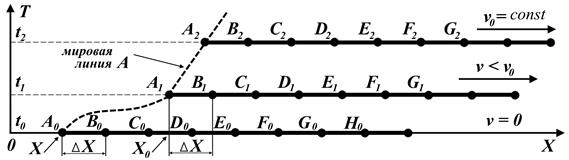
Рис.8.3 Иллюстрация к задаче с космонавтами [7, с.72]