Парадокс близнецов - обзор решений,
гл. 9 Тахионная теория относительности
Путенихин П.В.
![]()
![]()
![]()
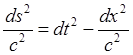
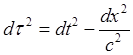
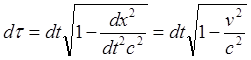
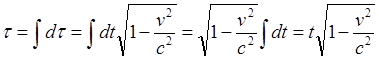 (9.1.1)
(9.1.1)
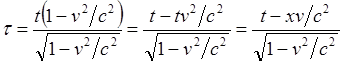
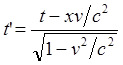
(9.1.2)
![]() (9.1.3)
(9.1.3)
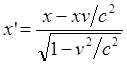 (9.1.4)
(9.1.4)
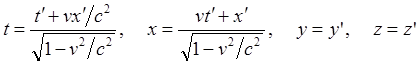
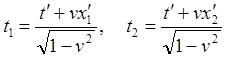
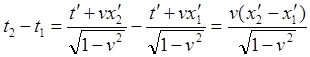
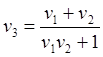
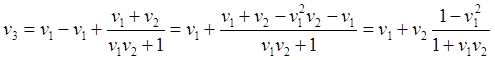
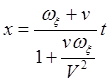
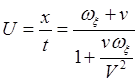
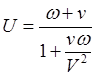
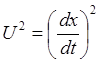
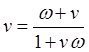
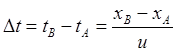 , (28)
, (28)
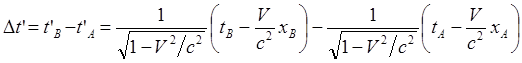 ,
,
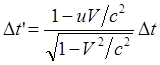 (29)
(29)
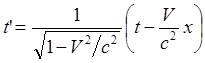
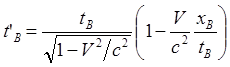
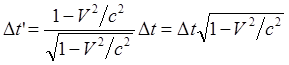 (29a)
(29a)
![]()
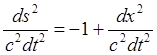
![]()
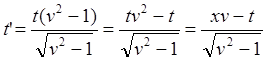
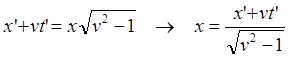
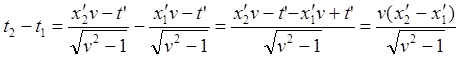
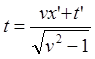
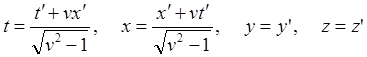
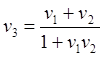
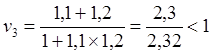
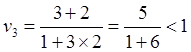
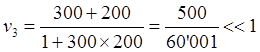
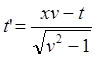
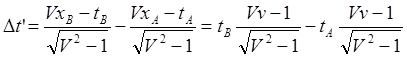
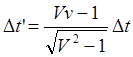
![]() (9.3.1)
(9.3.1)
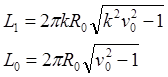
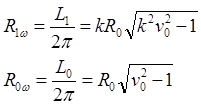 (9.3.2)
(9.3.2)
![]()
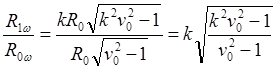
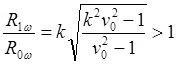 (9.3.3)
(9.3.3)
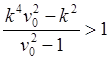
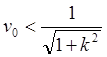
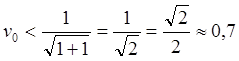
![]()
![]()
![]()
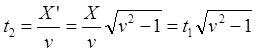
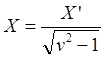
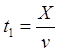
![]()
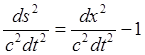
![]() (9.5.1)
(9.5.1)
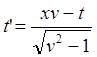 (9.5.2)
(9.5.2)
![]() (9.5.3)
(9.5.3)
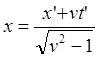 (9.5.4)
(9.5.4)
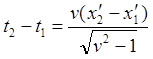
![]()
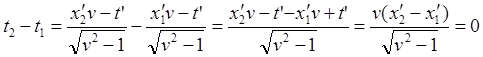
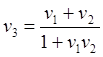
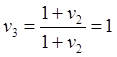
1. Maccarrone G.D., Recami E., Two-Body Interactions through Tachyon Exchange. \\Nuovo Cimento A, 57, 85 (1980)
2. Recami E., The Tolman-Regge Antitelephone Paradox: Its Solution by Tachyon Mechanics. \\Electronic Journal of Theoretical Physics (EJTP) 6, No. 21 (2009), 1-8.
3. Tolman R.C., The Theory of the Relativity of Motion. University of California Press, Berkeley, 1917. Press of the New Era Printing Company Lancaster.PA
4. Барашенков В.С., "Антимир скоростей. Тахионы", Журнал "Химия и жизнь", 1975, N 3, стр. 11-16.
5. Барашенков В.С., "Тахионы. Частицы, движущиеся со скоростями больше скорости света", УФН, 114 (1) 133 (1974)
6. Рашевский П.К., Риманова геометрия и тензорный анализ. Изд.3. - М., "Наука", 1967. - 664 с., ил.
7. Фейнберг Дж., Частицы, движущиеся быстрее света. В сборнике "Над чем думают физики", вып. 9. Элементарные частицы. Под ред. Суханова А.В., пер. с англ. В.П. Павлов, А.А. Славнов. - М.: Наука, 1973, с.90-104.
8. Эйнштейн А. "К электродинамике движущихся тел", Собрание научных трудов в четырех томах. Том 1. Статьи, рецензии, письма. Эволюция физики. М.: Наука, 1965.
9. Эйнштейн А., О специальной и общей теории относительности (Общедоступное изложение). В сборнике "Теория относительности". -- Ижевск: НИЦ "Регулярная и хаотическая динамика". -- 2000, 224 с.
10. Эйнштейновский сборник. 1973. - М.: Наука, 1974
11. Противоречие между квантовой механикой и СТО, 2010, URL:
12. Нелокальная квантовая передача классической информации, журнал "Точная наука", ИД "Плутон", вып.33 от 17 декабря 2018 г., URL:
13. Причина СТО - инвариантность скорости света, 2011, URL:
14. Противоречия принципа реинтерпретации, сборник статей XLI международной научной конференции "ТЕХНОКОНГРЕСС", ИД "Плутон", 8 апреля 2019, URL:
15. Решение парадокса Эренфеста, журнал "Точная наука", ИД Плутон, вып.36 от 14 января 2019, URL:
16. Сверхсветовой зайчик против тахиона, 2013, URL:
17. СТО неприменима к сверхсветовым сигналам, 2014, URL: