Парадокс близнецов - обзор решений,
гл.10 Формула сложения скоростей в ТТО
Путенихин П.В.
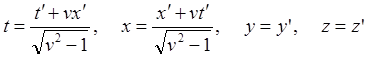
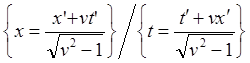
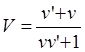
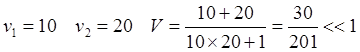
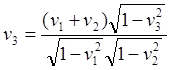 (6.6)
(6.6)
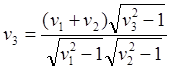 (10.1)
(10.1)
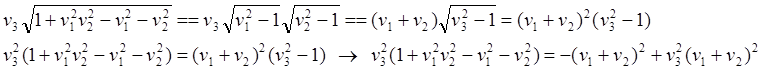
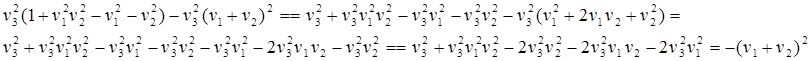
![]()
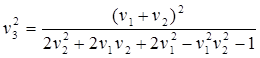
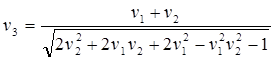
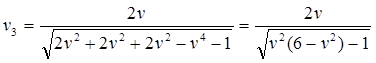
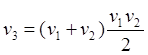
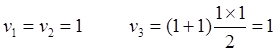
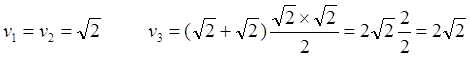
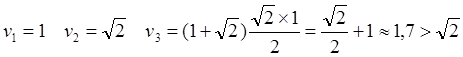
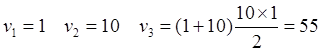
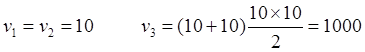
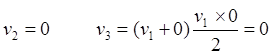

Рис.10.1. Начальное положение попутно движущихся тахионных ИСО
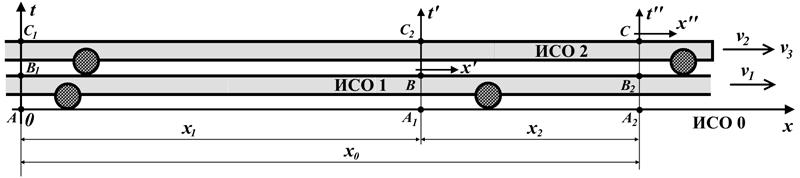
Рис.10.2. Конечное положение движущихся тахионных ИСО
![]() (10.2)
(10.2)
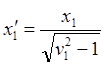
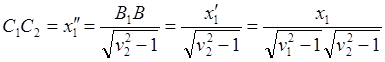
![]() (10.3)
(10.3)
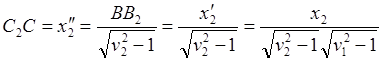
![]() (10.4)
(10.4)
![]() (10.5)
(10.5)
![]()
![]() (10.6)
(10.6)
![]()
![]() (10.7)
(10.7)
![]()
![]()
![]() (10.8)
(10.8)
![]()
![]()
![]()
![]()

Рис.10.3. Новые обозначения тахионных ИСО и скоростей
![]() (10.9)
(10.9)
![]() (10.10)
(10.10)

Рис.10.4. Считаем неподвижной тахионную ИСО B
![]()
![]()
![]()
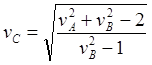 (10.11)
(10.11)
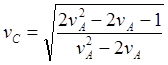
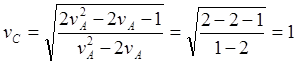
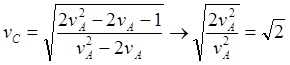
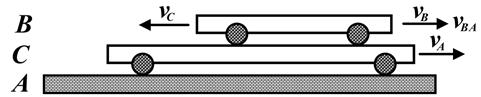
Рис.10.5. Считаем "несущей" ИСО C
![]()
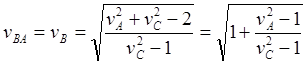 (10.12)
(10.12)
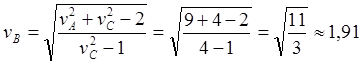
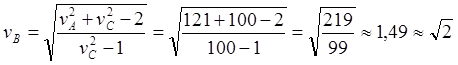
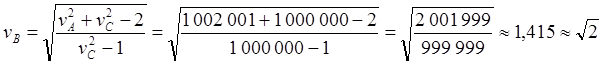
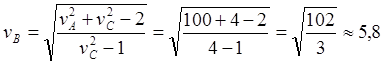
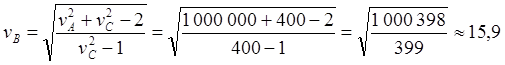

Рис.10.6. Новые обозначения ИСО и скоростей в СТО
![]() (10.13)
(10.13)
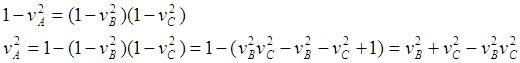
![]() (10.15)
(10.15)
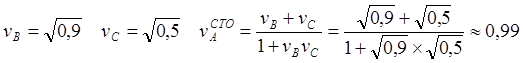
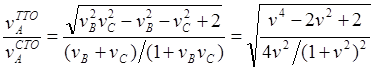
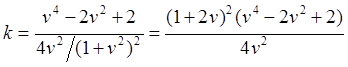
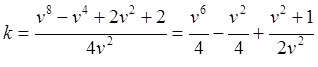
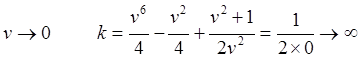
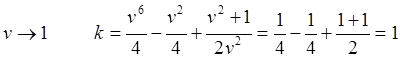
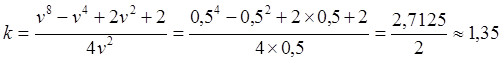

Рис.10.7. Копия рис.10.4. Считаем в СТО неподвижной ИСО B
![]()
![]()
![]()
![]()
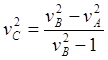
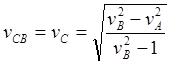 (10.16)
(10.16)
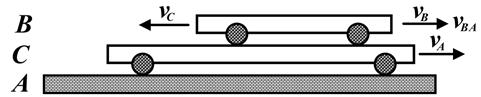
Рис.10.5. Считаем "несущей" ИСО C
![]()
![]()
![]()
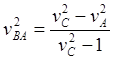
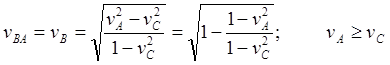 (10.17)
(10.17)
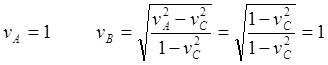
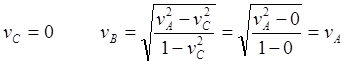
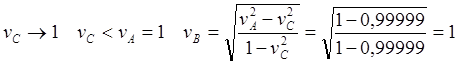
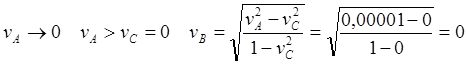
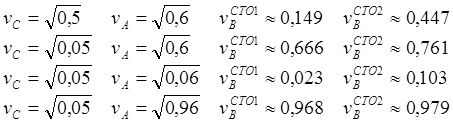
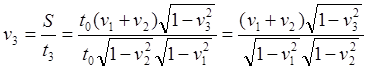 (6.6)
(6.6)
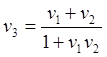
![]()
, (10.13)
![]() (10.15)
(10.15)
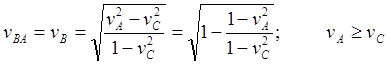 (10.17)
(10.17)
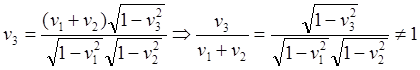 (6.6a)
(6.6a)
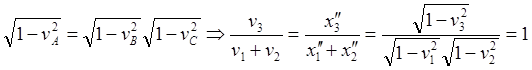 (10.14)
(10.14)
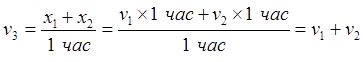
![]() (10.18)
(10.18)

Рис.6.1. Сложение разных скоростей встречно движущихся ИСО
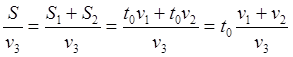
![]()
![]()
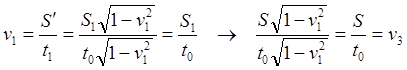
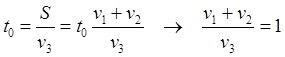
![]()
![]()
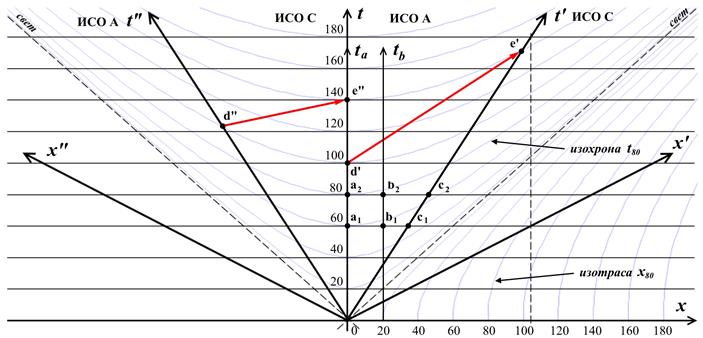
Рис.10.7. Диаграмма Минковского - изохроны и изотрасы
![]()
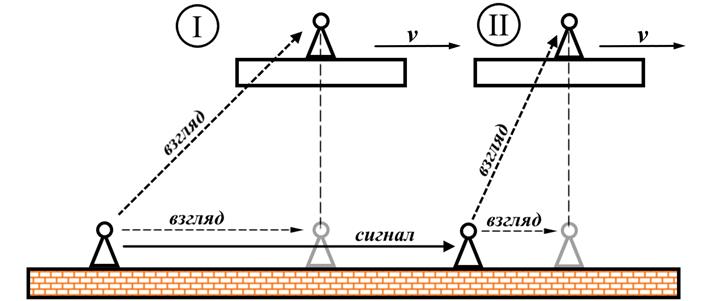
Рис.10.8. Эквивалентность параллельного движения и движения вдоль одной линии
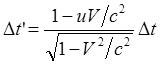
(29)
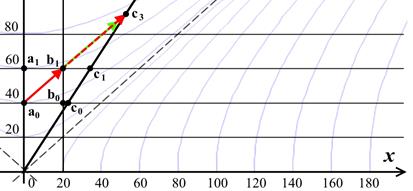
Рис.10.9. Исследование световой сигнализации в прошлое на диаграмме Минковского при попутном направлении сигнала и движущейся ИСО
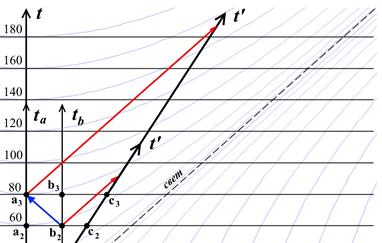
Рис.10.10. Исследование световой сигнализации в прошлое на диаграмме Минковского при противоположном направлении сигнала и движущейся ИСО
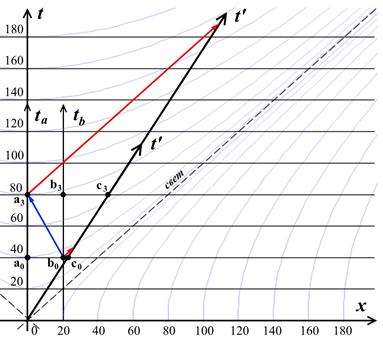
Рис.10.11. Исследование досветовой сигнализации в прошлое на диаграмме Минковского
![]() (10.12)
(10.12)
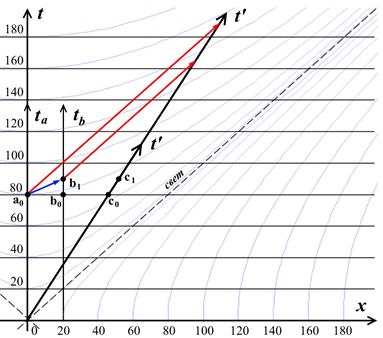
Рис.10.12. Исследование сверхсветовой сигнализации в прошлое на диаграмме Минковского
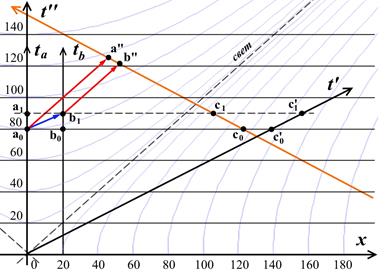
Рис.10.13. Диаграмма Минковского - исследование сигнализации в прошлое в ТТО
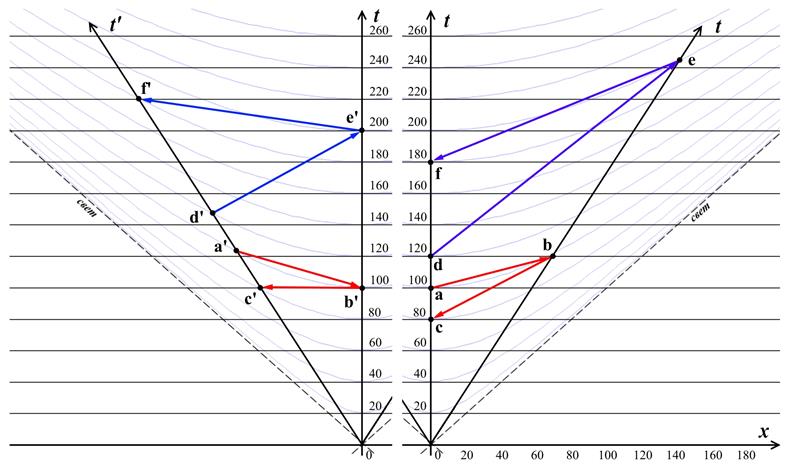
Рис.10.14. Сигнализация в прошлое на диаграмме Минковского
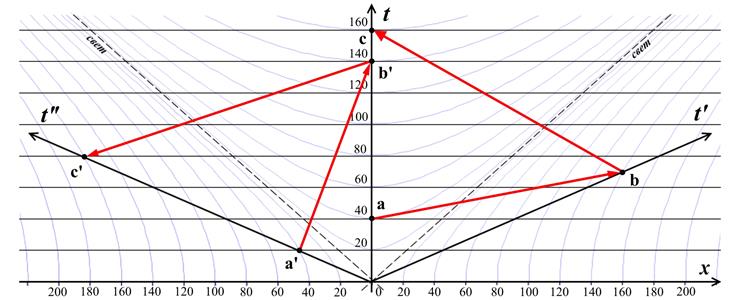
Рис.10.15. Сигнализация в прошлое в ТТО на диаграмме Минковского
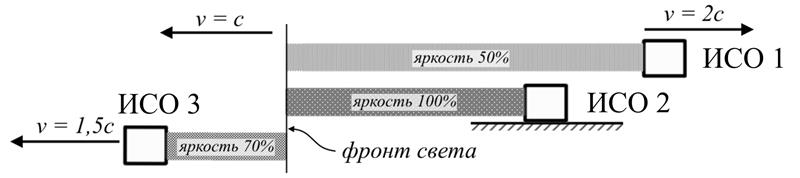
Рис.10.16. Демонстрация 2-го постулата в тахионной ТО