Парадокс близнецов - обзор решений,
гл.11 Приложения
Путенихин П.В.
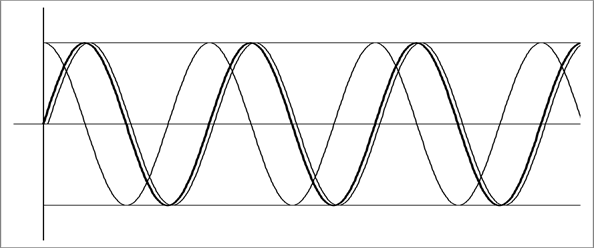
Рис.11.1 Числовой интеграл функции cos(x)
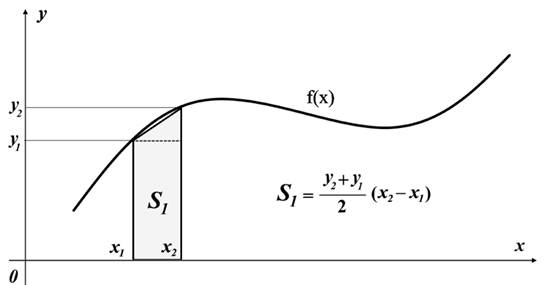
Рис.11.2 Площадь интегральной трапеции
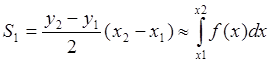
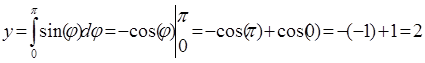
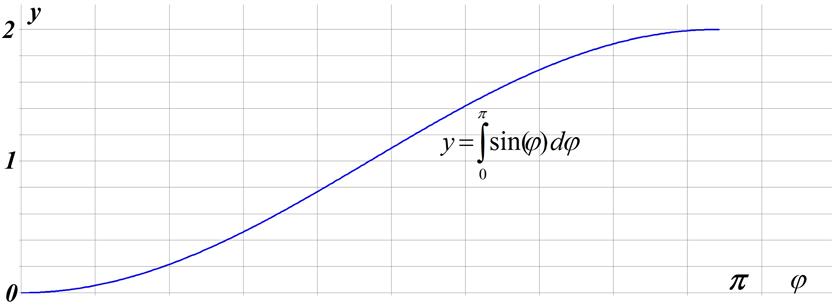
Рис.11.3 Численное интегрирование уравнения Sin(x)
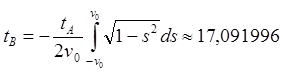 (11.1)
(11.1)
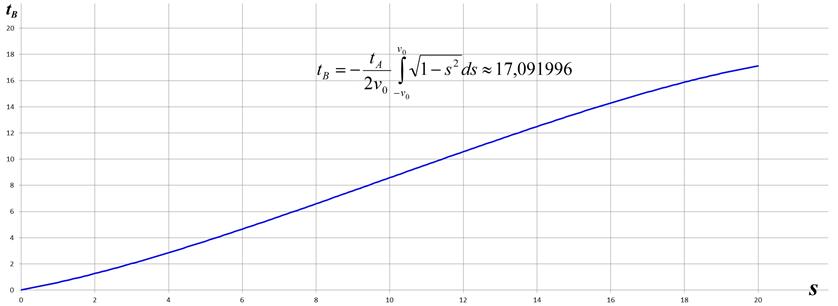
Рис.11.4 Численное интегрирование уравнения (11.1)