14. Уравнения движения в расширяющейся Вселенной
14.1. Закон Хаббла в формализме ОТО
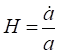 (14.1)
(14.1)
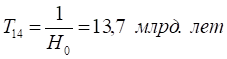
![]()
![]() (14.2)
(14.2)
![]()
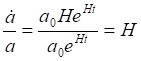
![]()
![]() (14.3)
(14.3)
![]()
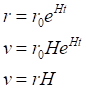 (14.4)
(14.4)
![]() (14.5)
(14.5)
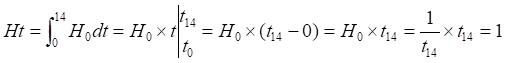
![]()
![]() (14.6)
(14.6)
14.2. Закон Хаббла в физике Ньютона
![]()
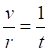
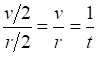
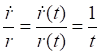
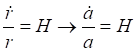
![]()
![]()
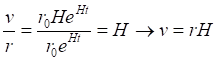
14.3. Закон Хаббла в философии
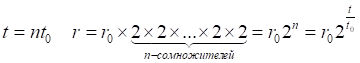
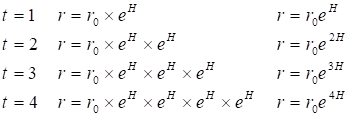
![]() (14.7)
(14.7)
![]() (14.8)
(14.8)
![]()
![]()
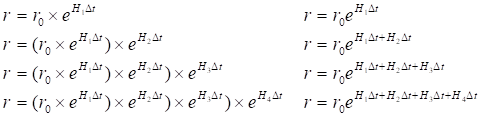
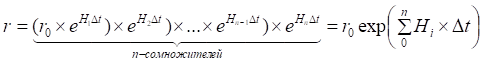
![]()
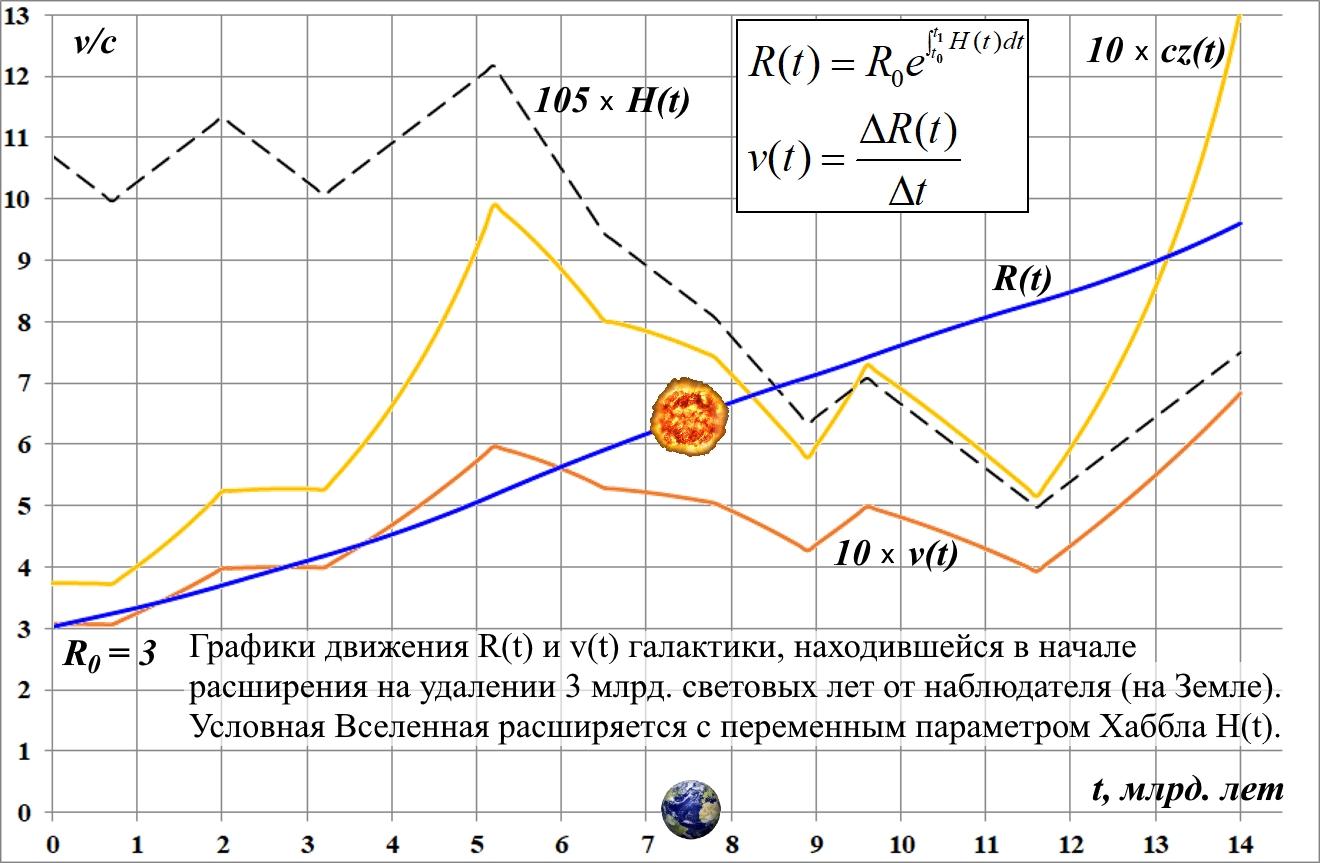
Рис.14.1. Пример диаграмм движения для переменного H(t)
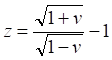
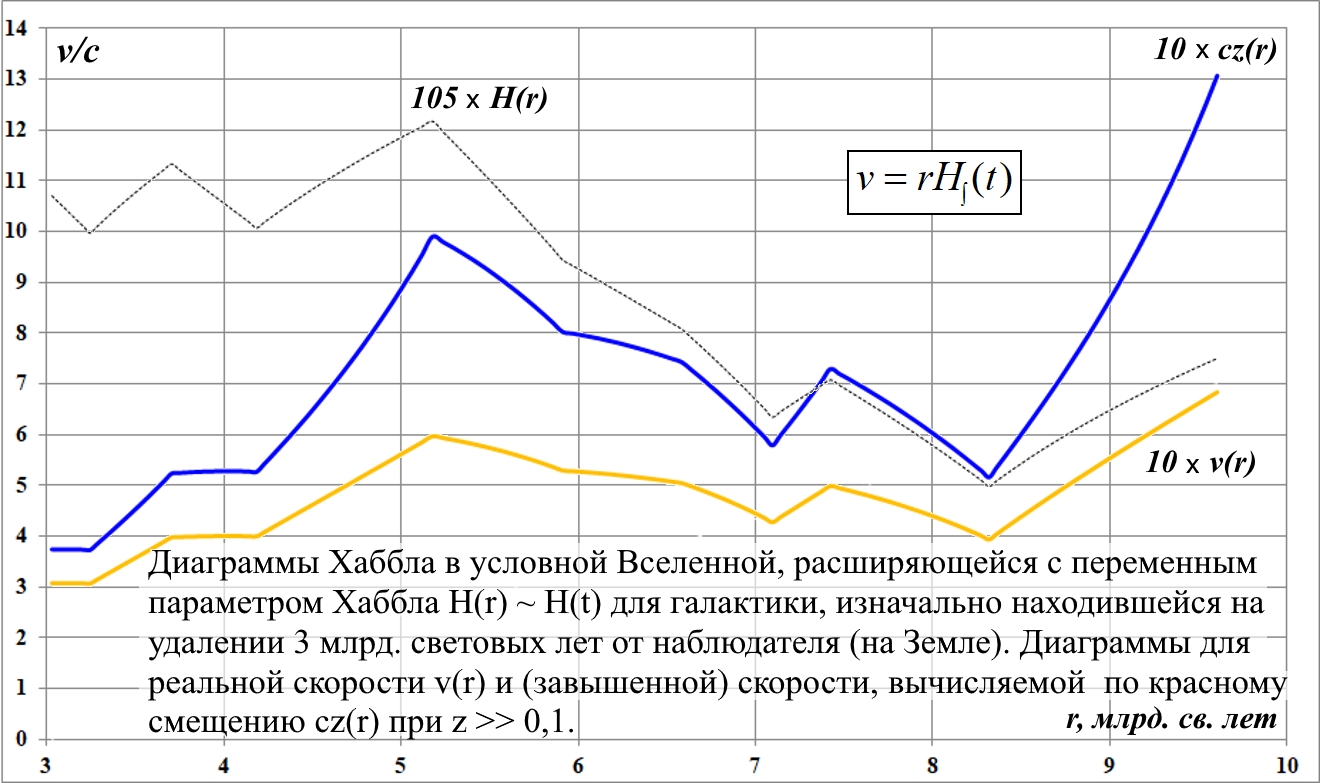
Рис.14.2. Диаграммы Хаббла для v(r) и cz(r) во Вселенной с параметром Хаббла H(r)
Литература
Предыдущие: http://samlib.ru/p/putenihin_p_w/accele01.shtml
http://samlib.ru/p/putenihin_p_w/accelerate74.shtml
http://samlib.ru/p/putenihin_p_w/accele02.shtml
http://samlib.ru/p/putenihin_p_w/dc11.shtml
http://samlib.ru/p/putenihin_p_w/dc13.shtml
Текущая: http://samlib.ru/p/putenihin_p_w/dc14.shtml
Следующая: http://samlib.ru/p/putenihin_p_w/dc12.shtml
|