Путенихин Петр Васильевич. Решение парадокса Эренфеста, дополнения

Дополнения и анимации к статье "Решение Парадокса Эренфеста" в журнале "Точная наука" Издательского дома "Плутон" вып.36 от 14 января 2019, с.8-22.

Полный текст статьи размещён на портале eLibrary, URL:
https://elibrary.ru/contents.asp?id=36825393 с.8-22

http://samlib.ru/p/putenihin_p_w/erenfest-dop.shtml - данная статья

В статье приводится решение парадокса колеса - парадокса Эренфеста. Показано, что парадокс является мнимым. В отношении вращающегося колеса специальная теория относительности делает непротиворечивые предсказания. Формулировки парадокса имеют ошибки.

Содержание парадокса

Основное "назначение" множества парадоксов СТО - это показать внутренние противоречия теории. Если теория делает предсказания о каком-либо явлении, которые противоречат друг другу, то это свидетельствует об ошибочности теории, что требует её пересмотра. Парадоксы СТО выводятся из мысленных экспериментов, то есть, воображаемого эксперимента на основе положений теории. Одним из таких парадоксов по праву считается один из старейших парадоксов - парадокс Эренфеста от 1909 года, в настоящее время часто формулирующийся как "парадокс колеса" и который по утверждениям многих авторов до настоящего времени не имеет удовлетворительного объяснения, решения.

В литературе приводятся несколько различающихся формулировок "парадокса" Эренфеста. Здесь в кавычки слово парадокс поставлено умышленно, поскольку в данной заметке будет показано, что парадокс сформулирован с ошибками, на основе утверждений, приписываемых специальной теории относительности, но которых она не делает. Обобщенно эти различные формулировки парадокса можно свести к трем группам:

- при вращении колеса спицы деформируются;

- невозможно вообще раскрутить колесо из абсолютно твердого материала;

- при раскрутке со световой скоростью (обода) колесо стягивается в точку, исчезает.

Все эти формулировки в своей сути достаточно близки друг к другу и при некоторых условиях объединяются. Например, в работе "Теория относительности в элементарном изложении" приводится такая формулировка:

"Вначале колесо неподвижно, а затем приводится в столь быстрое вращение, что линейная скорость его краев приближается к световой. При этом участки обода ... сокращаются ... , тогда как радиальные "спицы" ... сохраняют свою длину (ведь релятивистское укорочение испытывают только продольные размеры, т. е. размеры в направлении движения)" [3].

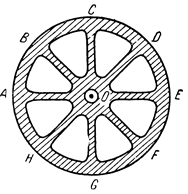
Ehrenfest

Рис.1. Иллюстрация к парадоксу колеса в работе [3]

И затем приводится решение сформулированного парадокса:

"... когда неподвижное вначале колесо приводится в быстрое вращение: его обод стремится сократиться, а спицы - сохранить неизменную длину. Какая из этих тенденций возьмет верх - всецело зависит от механических свойств обода и спиц; но никакого укорочения обода без пропорционального ему укорочения спиц не будет (разве что колесо примет форму сферического сегмента). Очевидно, что с принципиальной точки зрения ничто не изменится также и в том случае, если колесо со спицами будет заменено сплошным диском" [3].

Суть решения, как видим, состоит в том, что либо спицы обязательно сократятся, либо обод вытянется, в зависимости, от жесткости материала. Видимо, при однородности материала сокращение будет взаимным: сократятся и спицы и обод, но в меньшей мере.

Парадокс колеса в версии Эренфеста приводится в работе "Неисправленная ошибка Пуанкаре и анализ СТО" [2]:

"Рассмотрим плоский, твердый диск, вращающийся вокруг своей оси. Пусть линейная скорость его края по порядку величины сравнима со скоростью света. Согласно специальной теории относительности, длина края этого диска должна испытывать лоренцово сокращение ... В радиальном направлении лоренцова сокращения нет, поэтому радиус диска должен сохранять свою длину. При такой деформации диск технически уже не может быть плоским. Угловая скорость вращения уменьшается с увеличением расстояния от оси вращения. Поэтому соседние слои диска должны скользить друг относительно друга, а сам диск будет испытывать деформации кручения. Диск с течением времени должен разрушиться" [2].

Трактовка, следует заметить, весьма специфическая: разрушение связывается не со сжатием внутренних слоёв или спиц, а с их изгибом, закручиванием. Причину возникновения разности угловых скоростей автор не объясняет, ссылаясь на Эренфеста, и лишь добавляя:

"Сами релятивисты не смогли привести никаких объяснений физических причин ни для объяснения гипотезы, ни для объяснения парадокса" [2].

Однако, это единственное описание эффекта скручивания диска, которое мне встретилось в интернете при беглом просмотре.

Википедия описывает парадокс следующим образом, приводя в тексте ссылку на детскую энциклопедию:

"Рассмотрим окружность (или полый цилиндр), вращающуюся вокруг своей оси. Так как скорость каждого элемента окружности направлена по касательной, то она (окружность) должна испытывать лоренцево сокращение, то есть её размер для внешнего наблюдателя должен казаться меньше, чем её собственная длина. ... изначально неподвижная жёсткая окружность после её раскручивания должна парадоксальным образом уменьшать свой радиус, чтобы сохранить длину. По рассуждениям Эренфеста абсолютно твёрдое тело невозможно привести во вращательное движение, поскольку в радиальном направлении лоренцева сжатия быть не должно. Следовательно, диск, бывший в покоящемся состоянии плоским, при раскручивании должен как-то изменить свою форму" [4].

Здесь указывается ещё одно проявление парадокса со ссылкой на Эренфеста: абсолютно твердый диск вообще невозможно привести во вращение. Подобная же трактовка приведена и в "Энциклопедии для детей", которая, в свою очередь, ссылается на авторскую работу Эренфеста - короткую заметку "Равномерное вращательное движение тел и теория относительности" от 1909 года:

"Заметка содержала парадоксальное утверждение: абсолютно твердый цилиндр (или диск) невозможно привести в быстрое вращательное движение вокруг центральной оси, в противном случае возникает противоречие частной теории относительности. В самом деле, пусть такой диск вращается, тогда длина его окружности вследствие лоренцева сокращения уменьшится, а радиус диска останется постоянным ... При этом отношение длины окружности диска к диаметру уже не равняется числу n. Этот мысленный эксперимент и составляет содержание парадокса Эренфеста" [8].

Здесь, можно сказать, приводится основная, общепринятая формулировка парадокса Эренфеста, отличающаяся от распространенной формулировки парадокса колеса. В ней уже не говорится о деформации диска или спиц колеса. Просто диск будет оставаться неподвижным.

В работе "Тайны космоса" без указания ссылки на источник приведены размышления Эренфеста:

"... проведем опыт с диском. Будем вращать его, постепенно увеличивая скорость. Размеры диска... будут уменьшаться; кроме того, диск искривится. Когда же скорость вращения достигнет скорости света, он попросту исчезнет. И куда только денется?" [1].

На приведённом далее рисунке искривлённый диск изображен с четырьмя спицами, изогнувшимися в виде подобия свастики и подписью к нему:

"диск при вращении должен был деформироваться, как показано на рисунке" [7].

То есть, как и выше делается вывод о деформации спиц, при этом, очевидно, вполне обоснованно предполагается, что твёрдость обода превышает гибкость спиц.

Наконец, чтобы выяснить, какая из формулировок парадокса соответствует авторской, приведём описание парадокса, как он сформулирован в упомянутой работе Эренфеста. Приводимая ниже цитата практически составляет всё содержание той краткой заметки:

"Оба определения не абсолютной твердости являются -- если я правильно понял -- эквивалентными. Поэтому достаточно указать на простейший вид движения, для которого данное первоначальное определение уже приводит к противоречию, а именно на равномерное вращение вокруг неподвижной оси. В самом деле, пусть имеется не абсолютно твердый цилиндр C с радиусом R и высотой Н. Пусть он постепенно приводится во вращение вокруг своей оси, происходящее затем с постоянной скоростью. Назовем R' радиус, который характеризует этот цилиндр с точки зрения неподвижного наблюдателя. Тогда величина R' должна удовлетворять двум противоречащим друг другу требованиям:

а) длина окружности вращающегося цилиндра по сравнению с состоянием покоя должна сократиться:

2πR'<2πR,

поскольку каждый элемент такой окружности движется в направлении касательной с мгновенной скоростью R'ω;

б) мгновенная скорость какого-либо элемента радиуса перпендикулярна его направлению; это значит, что элементы радиуса не подвергаются никакому сокращению по сравнению c состоянием покоя. Отсюда следует, что

R'=R

Замечание. Если считать, что деформация каждого элемента радиуса определяется не только мгновенной скоростью центра тяжести, но также и мгновенной угловой скоростью этого элемента, то необходимо, чтобы функция, описывающая деформацию, содержала кроме скорости света с еще одну универсальную размерную константу, или же в нее должно входить ускорение центра тяжести элемента" [9].

Как видим, по крайней мере, в первоначальной авторской версии парадокс прямо касается не абсолютно твердых тел. Ничего не говорится о скручивании слоёв. Ничего об "исчезновении" диска. Возможно, все эти расширения первоначальной идеи сформулированы где-то в последующих работах Эренфеста, но оставим это всё на совести цитированных авторов: проверяемых ссылок на свои утверждения они не привели. Таким образом, мы вполне обоснованно можем рассмотреть:

Миф о парадоксе Эренфеста

Рассмотрим по возможности современные версии парадокса, указанные в начале статьи. Простейшей и, видимо, самой распространенной, является версия "парадокс колеса", с которой, как можно заметить, в наибольшей степени совпадает и противоречие, сформулированное в 1909 году Эренфестом. По сути, парадокс Эренфеста и является тождественно парадоксом колеса.

Однако, сначала мы рассмотрим его предельную версию. Это версия, в которой спицы или внутренняя часть колеса не вращаются вообще. В этом случае мы избавляемся от всяких сомнений о том, сокращаются спицы или не сокращаются. Такое "колесо", как можно догадаться, имеет вид полого тонкостенного цилиндра или тонкого кольца, насаженного на толстую ось. Решение такого "парадокса" очевидно. И вновь, как выше, слово "парадокс" здесь взято в кавычки исключительно по причине того, что это, собственно, и не парадокс, а псевдо, мнимый парадокс. Специальная теория относительности описывает поведение такого колеса без каких-либо противоречий. Действительно, с точки зрения неподвижной оси "обод" колеса при вращении испытывает лоренцево сокращение, что приводит к уменьшению его диаметра. С этой точки зрения либо колесо лопнет, либо оно сожмёт ось, выдавив на ней выемку, либо при достаточной упругости кольцо растянется. В этом случае внешний наблюдатель не заметит никаких изменений, даже если колесо-кольцо будет раскручено до световой скорости: лишь бы материалу колеса хватило запаса упругости.

Теперь перейдём в систему отсчета колеса-обода. Очевидно, что невозможно привязать систему покоя ко всему колесу, поскольку векторы скоростей точек направлены в разные стороны. В покое может быть одновременно лишь одна точка, касающаяся неподвижной поверхности. Понятно, что такое "неподвижное" колесо - это просто колесо, катящееся по неподвижной поверхности. О нём мы только-то и можем сказать, что скорость его центра равна половине скорости элемента на верхней части. Но это замечание вдруг неожиданно напоминает нам уже рассмотренный парадокс - парадокс транспортера [5]. Действительно, в том парадоксе тоже есть три точки: неподвижная; верхняя, движущаяся с некоторой скоростью и средняя, движущаяся с половинной от верхней скоростью. Что может быть общего между колесом и транспортером?

Однако, присмотримся повнимательнее. Посмотрим на колесо под углом к его оси. Чем этот угол больше, тем сильнее "сплющивается" колесо, принимая вид вытянутого эллипса, что довольно заметно напоминает транспортер.

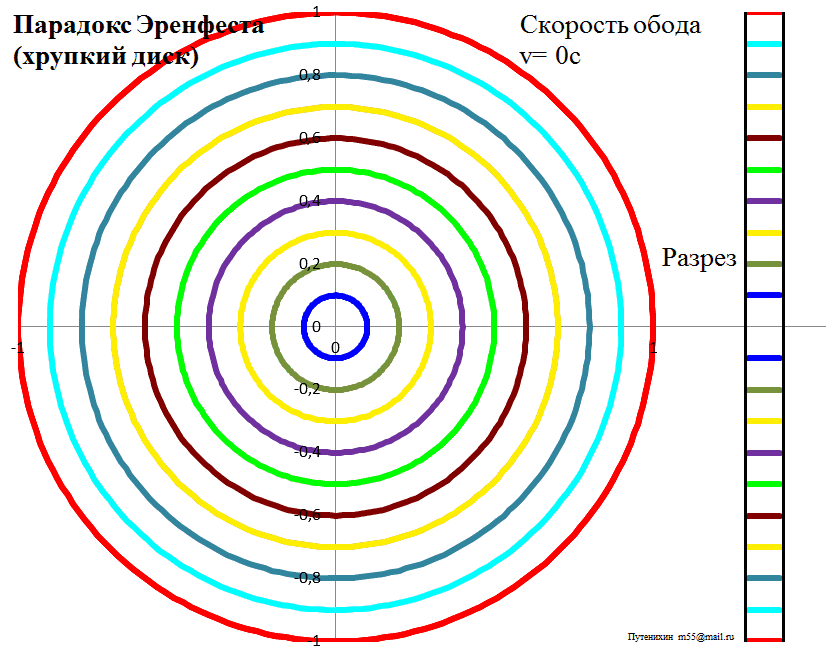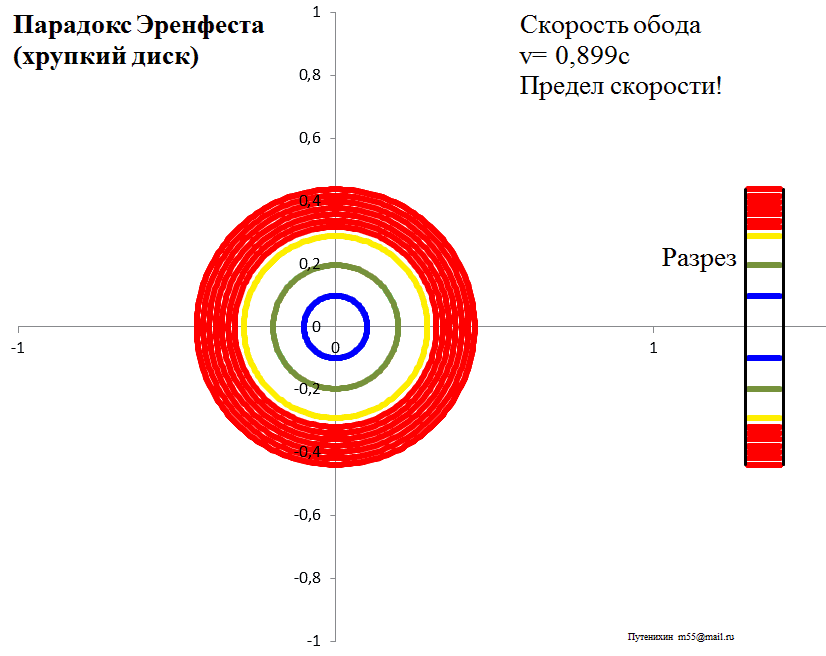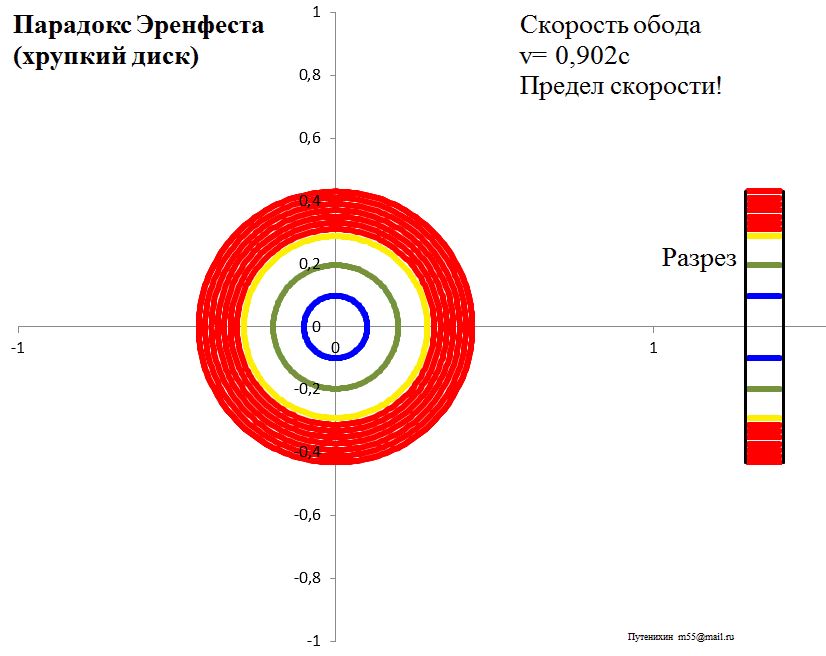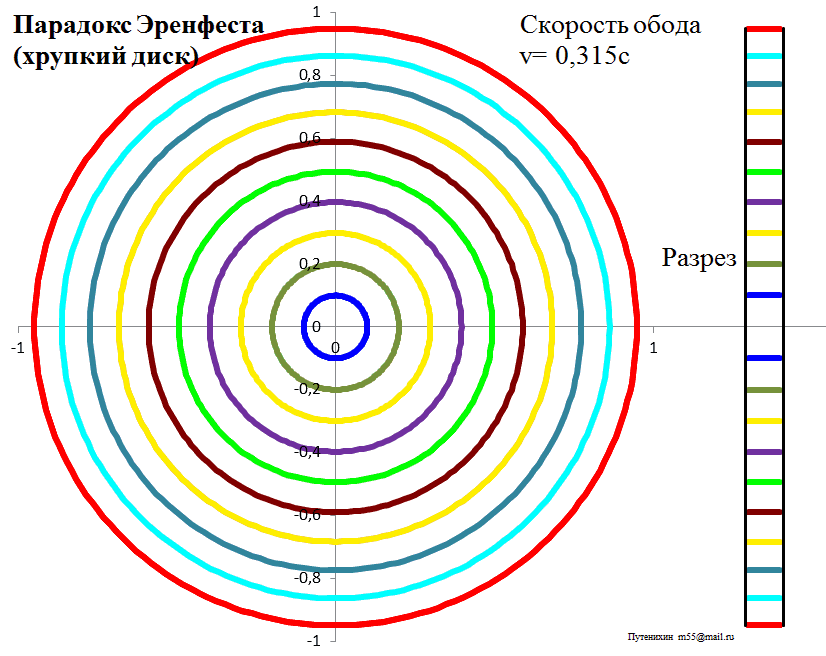
Ehrenfest

Рис.2. Если смотреть на колесо под большим углом, оно выглядит как эллипс. Окружность из утолщенной линии - это внешняя поверхность оси колеса. Тонкая красная окружность - вращающийся обод (колесо).

Хотя на получившемся транспортере лента - обод колеса движется по эллиптической траектории, мы вполне можем рассматривать "проекцию" этого обода на горизонтальную ось. В этом случае мы получаем вполне допустимую аналогию задачи о транспортерной ленте и её очевидное решение:

"В обоих случаях, и с точки зрения балки (станины) и с точки зрения ... ленты, результатом будет натяжение ленты, приводящее либо к деформации ... станины, либо к деформации ... ленты. В зависимости от начальных условий: что будет задано более прочным. Парадокс транспортера оказался мнимым, кажущимся парадоксом [5].

Обод колеса, видимый как транспортерная лента, как и в задаче о транспортере будет сокращаться, что неизбежно приведёт либо к его разрыву, либо к деформации оси, которая под выбранным углом выглядит как станина транспортера. Понятно, что ось может быть сегментированной, то есть состоять из спиц, которые, как и сплошная ось, будут деформированы, если обод окажется прочнее.

Таким образом, вариант "парадокса" колеса с тонким ободом и неподвижной осью парадоксом не является, поскольку теория относительности делает о нём непротиворечивые предсказания.

Теперь перейдём к сплошному диску. Более того, будем считать его абсолютно твердым, то есть, рассмотрим вариант парадокса Эренфеста о невозможности раскрутки такого диска.

Ниже приведена анимация рис.2 в статье. Для того чтобы выяснить, что произойдёт с колесом после превышения внешним ободом скорости 0,7 от скорости света, изменим форму колеса так, чтобы слои не мешали друг другу. Сдвинем слои колеса вдоль оси, превратив колесо в тонкостенный конус, воронку. Теперь при сжатии каждого слоя под ним нет других слоёв, и ничто не мешает ему сжиматься сколько угодно. Начнём раскручивать конус из состояния покоя до скорости 0,7 от скорости света и затем до скорости света, после чего уменьшим скорость в обратной последовательности. Изобразим этот процесс в виде анимации:

Ehrenfest

Рис.2а. Лоренцева деформация конуса при раскручивании. Слева вид вдоль оси конуса - воронки, справа - вид сбоку, перпендикулярно к оси.

На рисунке конус (воронка) показан в двух видах: вдоль оси, как всегда изображается парадокс колеса, и перпендикулярно к оси, вид сбоку, на котором виден "профиль" конуса. На виде сбоку мы отчетливо видим поведение каждого слоя-обода конуса, бывшего колеса. Каждый из этих слоёв изображен цветной линией. Эти линии повторяют соответствующие окружности, ободы, для которых построен график на предыдущем рисунке. Это позволяет увидеть каждый обод независимо от других и то, как внешний обод уменьшает свой радиус сильнее, чем внутренние.

Следует особо отметить следующие очевидные обстоятельства. Согласно теории относительности деформации диска или показанного конуса как таковой нет. Все изменения в его форме - это видимость для внешнего наблюдателя, с самим диском и конусом при этом ничего не происходит. Следовательно, он вполне может быть из абсолютно твердого материала. Изделия из такого материала не сжимаются, не растягиваются, не изгибаются и не скручиваются - они не подвержены никакой геометрической деформации. Поэтому видимость деформации вполне допускает и раскручивание этого диска до световой скорости. Внешний наблюдатель будет видеть, как показано на анимации, вполне логичную, хотя и довольно странную картину. Внешний обод конуса уменьшается до скорости 0,7с, после чего продолжает сжиматься дальше. При этом внутренний обод, который имел меньший радиус, оказывается с внешней стороны. Однако, это вполне очевидное явление. По раскрашенным ободам на анимации видно, как внешние ободы приближаются к центру диска, превращая конус в своеобразный замкнутый сосуд, амфору. Но нужно понимать, что при этом собственно конус остаётся таким, как и был изначально. Если уменьшить скорость его вращения, то все слои вернутся на свои места и амфора для неподвижного наблюдателя вновь превратится в конус. Это кажущееся перемещение слоёв, ободов вследствие сжатия к центру диска с точки зрения внешнего наблюдателя никак не связано с реальной геометрической деформацией самого диска. Потому-то и нет никаких физических препятствий для того, чтобы конус был изготовлен из абсолютно твердого материала.

Но это относится к конусу. А как поведёт себя плоское колесо, в котором все слои находятся всё-таки друг над другом? В этом случае неподвижный наблюдатель увидит весьма странную картину. После того как внешний обод диска уменьшится на скорости 0,7с, он сделает попытку дальнейшего сжатия. При этом внутренний обод, который имел меньший радиус, будет сопротивляться этому. Здесь мы напомним очевидное условие - при любой скорости диск должен оставаться плоским.

При всей странности картины можно достаточно легко догадаться о том, что произойдёт дальше. Нужно просто вспомнить рассмотренную выше картину с тонкостенным колесом, насаженным на неподвижную ось. Отличие лишь в том, что в рассмотренном случае неподвижная ось не испытывает лоренцева сокращения. Здесь же слои, он нуля до 0,7 от радиуса колеса, сами испытали сжатие и несколько уменьшили свои размеры. Не смотря на это внешние слои их всё равно "догнали". Теперь лоренцева сжатия внутренних слоёв недостаточно, они не дают внешним продолжить собственное сжатие. Как варианты мы можем выделить три сценария дальнейшего развития событий, не принимая во внимание действие центробежных сил и тот факт, что для такой раскрутки потребуется бесконечно мощный двигатель.

Для обычного материала при взаимодействии слоёв-ободов внутренние слои испытывают деформацию сжатия, а внешние - растяжения. Следовательно, более вероятен разрыв внешних ободов, чем упругое уменьшение объёма внутренних. Это очевидно, поскольку материал их один и тот же.

Ehrenfest

Рис.3а. Лоренцева деформация диска из обычного твердого материала

Здесь и на последующих анимация раскраска полос сделана наподобие "тельняшки" - более светлые цвета чередуются с более тёмными. В этом случае при сжатии диска на его разрезе лучше видно, что они не пересекают друг друга, а как бы складываются в виде "гармошки". На анимации сжатия обычного твердого (хрупкого) диска в красный цвет перекрашиваются слои (ободы), которые приходят в тесное соприкосновение, с силой давят друг на друга. В этом случае их материал испытывает как усилие на сжатие (внутренние слои), так и усилие на растяжение (внешние слои). При некоторых усилиях внешние слои, что более вероятно, просто будут разорваны, и разлетятся в разные стороны. Как видно на анимации, условия для разрыва наступают после достижения предельной скорости 0,7с.

Для абсолютно эластичного материала картина немного иная. В статье нет рисунка для этого случая, описанного на с.13. Разрыв слоёв невозможен, но возможно их бесконечное сжатие. Следовательно, при скорости внешнего обода, близкой к скорости света, для внешнего наблюдателя колесо может превратиться в бесконечно малую точку.

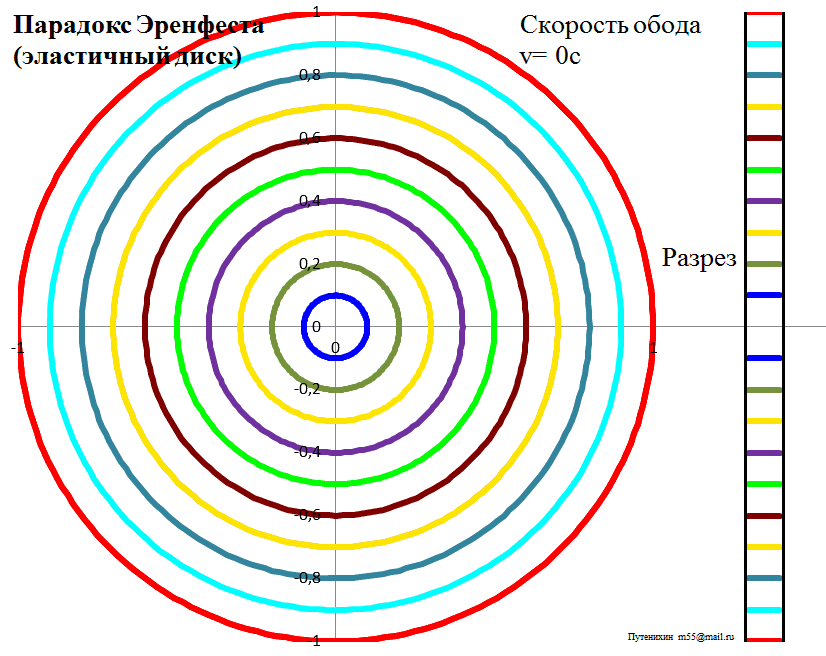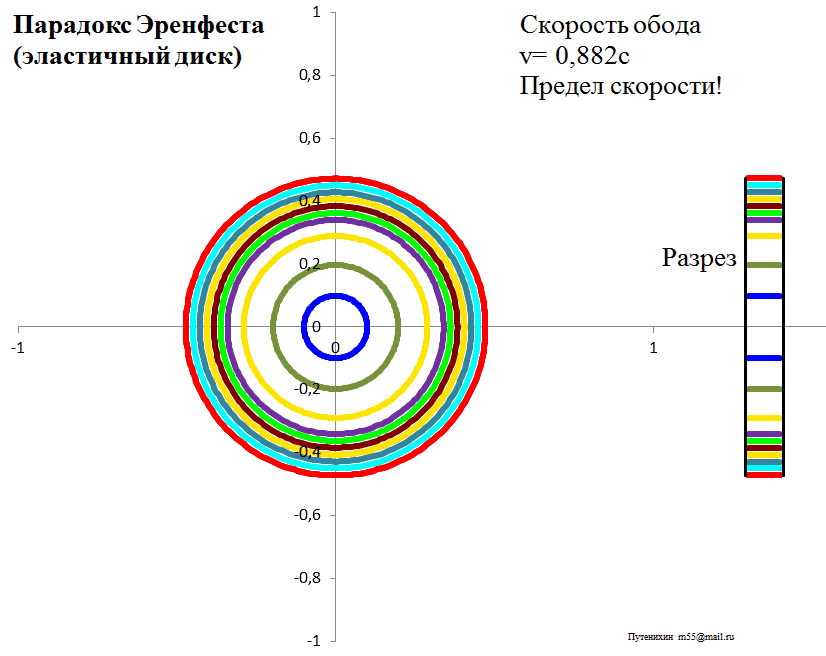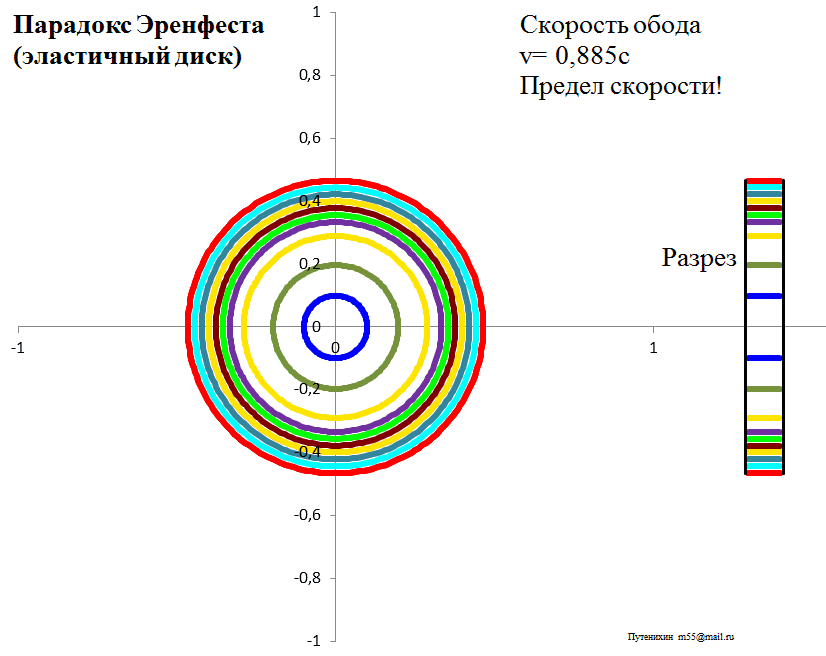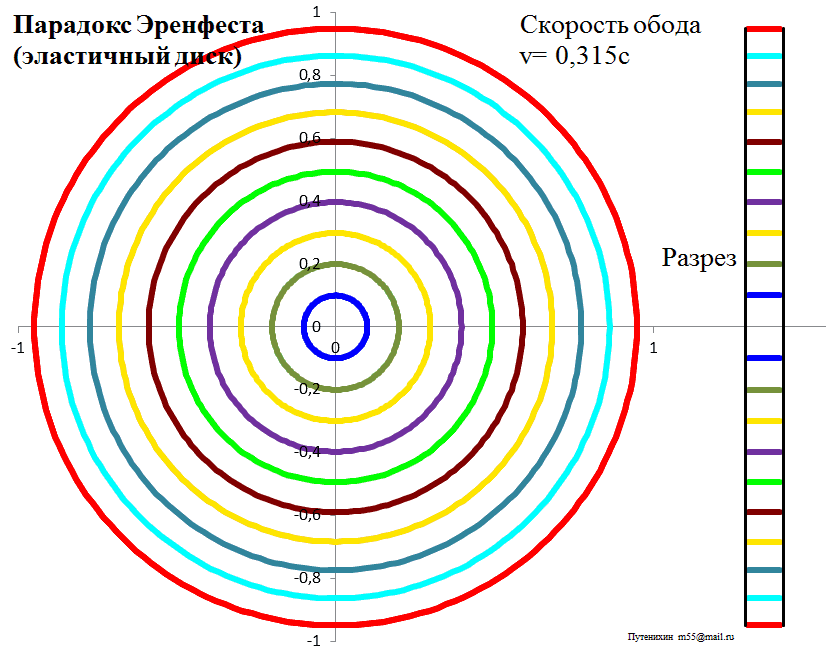
Ehrenfest

Рис.3б. Лоренцева деформация диска из эластичного материала

Это в том случае, если на сжатие будет необходимо меньшее усилие, чем на растяжение. Иначе форма колеса при равенстве этих сил будет оставаться неизменной. После прекращения вращения колесо примет свои первоначальные размеры без каких бы то ни было повреждений. На анимации, как и выше, видно, что слои-ободы складываются в виде "гармошки", не пересекая друг друга. Правда, здесь следовало бы показать утолщение диска в зазоре между внешним ободом и осью. Диск, очевидно, должен при сжатии принять форму бублика. При достижении скорости внешнего обода, равной скорости света, диск сожмётся в точку (вернее, в тонкую трубочку, надетую на ось).

Для абсолютно твердого материала колеса, который не сжимается, не растягивается и не изгибается, картина также будет отличаться от предыдущих. Этот рисунок в статье также отсутствует, а описание приведено на с.14.

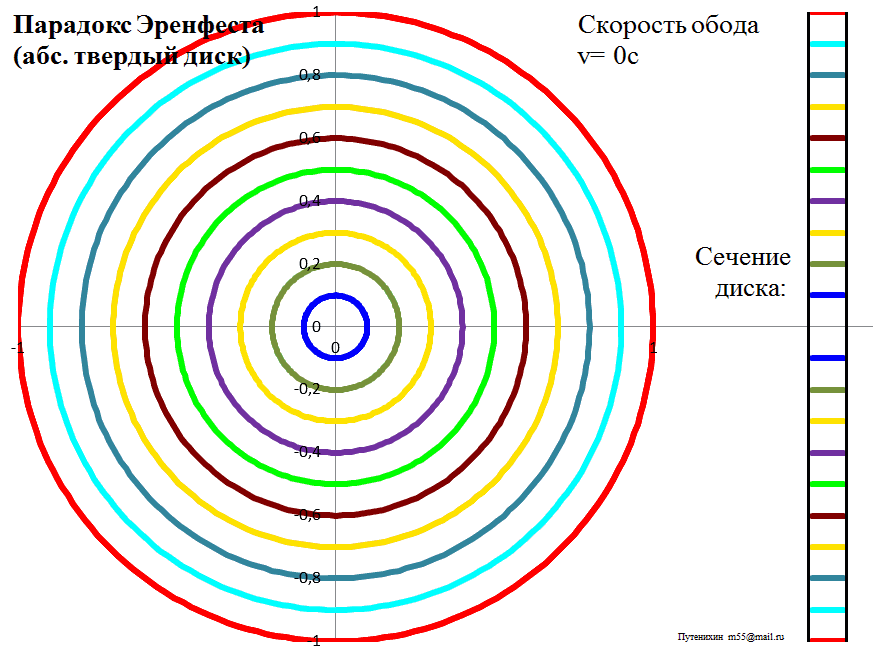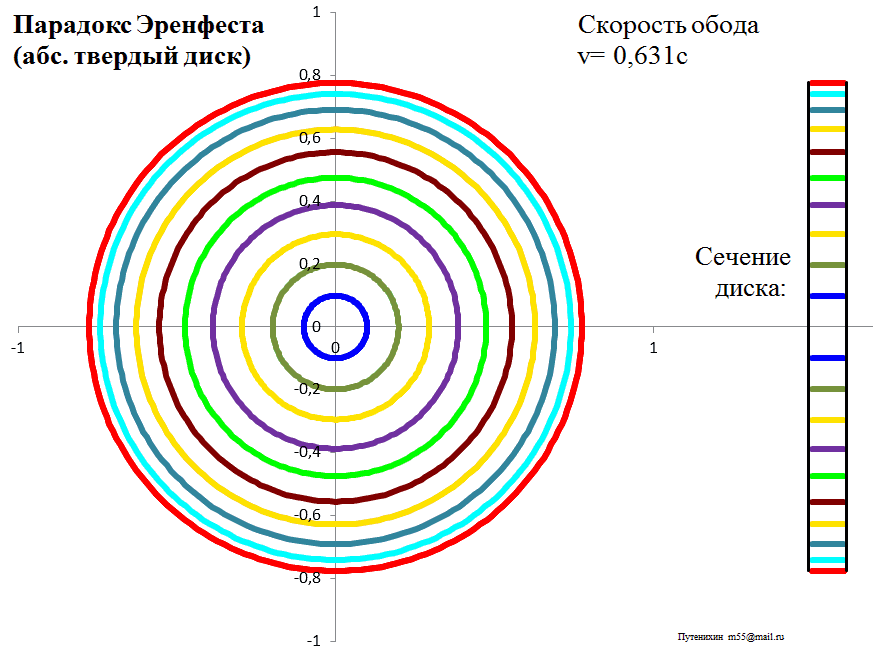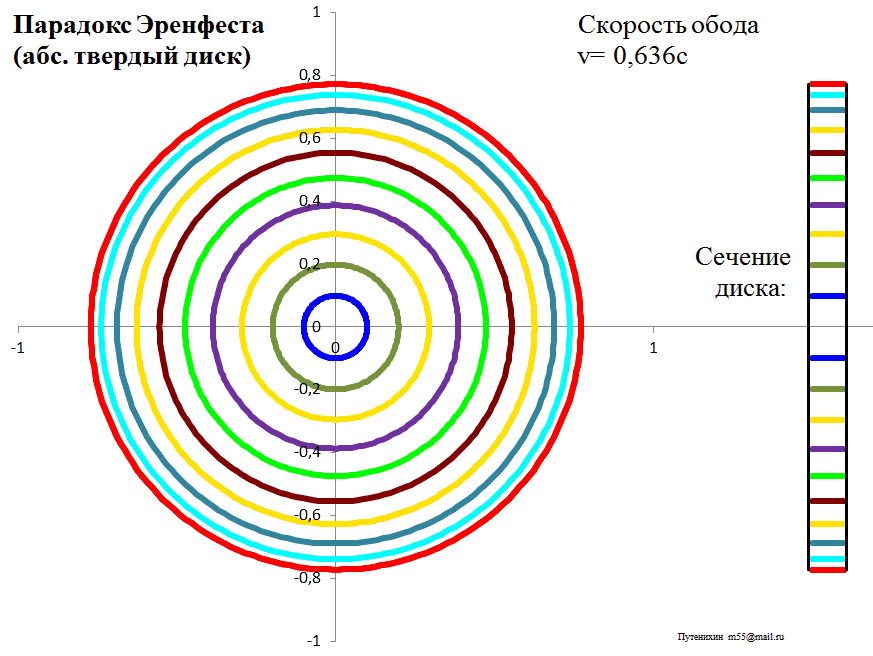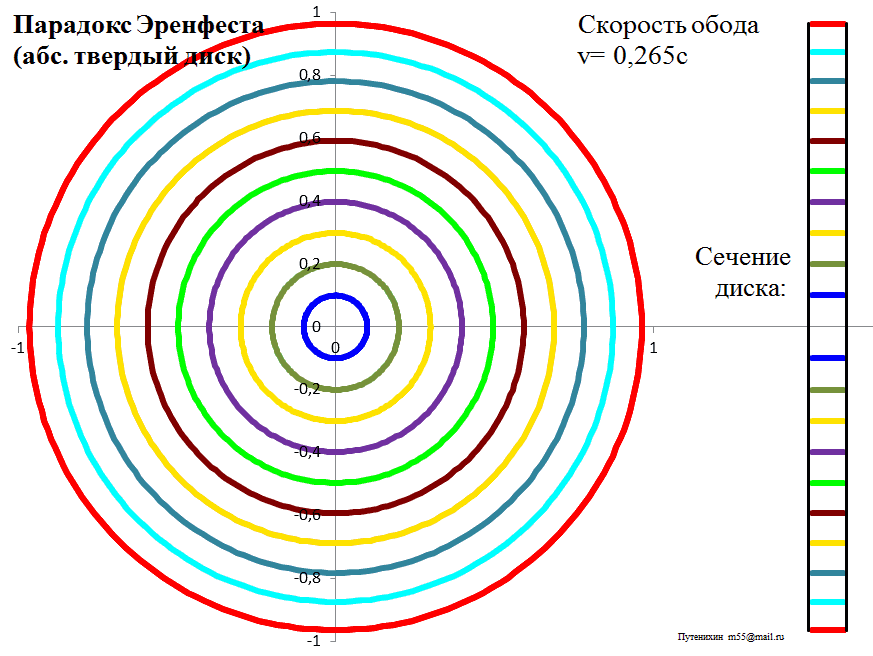
Ehrenfest

Рис.3в. Лоренцева деформация диска из абсолютно твердого материала

Внешние ободы не могут разорваться, а внутренние - сжаться. Поэтому, разрушения ни тех, ни других не будет, но будет стремительно возрастать сила их давления друг на друга после того, как будет достигнута предельная скорость вращения. За счет каких источников возникает эта сила? Очевидно, что за счет сил, приводящих колесо во вращение. Следовательно, внешний источник должен будет прикладывать всё большее и большее усилие вплоть до бесконечности. Понятно, что это невозможно, и мы приходим к выводу: при достижении внешним ободом абсолютно твердого колеса скорости -2/2 от скорости света дальнейшего увеличения этой скорости не будет. Приводной двигатель словно упрётся в стену. Это примерно то же самое, как бежать, например, за тракторной тележкой, прицепом. Можно бежать с любой скоростью, но при достижении тележки скорость будет сразу же ограничена её скоростью, скоростью трактора.

Приведённый здесь текст является укороченной версией статьи и отличается, главным образом, анимированными иллюстрациями.

Литература

1. Зигуненко С.Н., XX век: хроника необъяснимого. Тайны космоса: сенсации наших дней.- М.: Олимп; ООО "Фирма "Издательство ACT", 1998.- 480 с.

2. Кулигин В.А. Неисправленная ошибка Пуанкаре и анализ СТО, [резкая критика специальной теории относительности] URL:
http://n-t.ru/tp/to/sa.htm (дата обращения 21.01.2019)

3. Соколовский Ю.И. Теория относительности в элементарном изложении. - М.: Наука, 1964

4. Парадокс Эренфеста, Википедия, URL: https://ru.wikipedia.org/wiki/Парадокс_Эренфеста (дата обращения 21.01.2019)

5. Путенихин П.В. Мнимые парадоксы СТО. Парадокс транспортера, [Рассмотрен парадокс транспортера специальной теории относительности и его известное решение], URL:
http://samlib.ru/p/putenihin_p_w/paradox-transp.shtml (дата обращения 21.01.2019)

6. Путенихин П.В. Мнимые парадоксы СТО. Парадокс Эренфеста, [рассмотрен парадокс колеса или парадокс Эренфеста. В зависимости от материала колеса при раскручивании оно либо разрывается (твердое тело), либо сжимается до нулевых размеров (эластичное тело), либо препятствует раскручиванию быстрее 0.7 скорости света (абсолютно твердое тело)], URL:
http://samlib.ru/p/putenihin_p_w/paradox-ring.shtml (дата обращения 21.01.2019)

7. Реквием по теории?, "Спутник ЮТ", научно-популярный дайджест, #1/2002, URL: http://jtdigest.narod.ru/dig1_02/einstain.htm (дата обращения 21.01.2019)

8. Энциклопедия для детей. Том 16. Физика. ч.2. Электричество и магнетизм. Термодинамика и квантовая механика. Физика ядра и элементарных частиц / Глав.ред. В.А.Володин. - М.: Аванта+, 2000. - 432 с.: ил.

9. Эренфест П. - Относительность. Кванты. Статистика: Сборник статей. - М.: Наука, 1972, с.38

Комментарии: 1, последний от 03/07/2019. © Copyright Путенихин Петр Васильевич (pe_put@rambler.ru) Размещен: 29/12/2018, изменен: 20/03/2019. 25k. Статистика. Статья: Естествознание Дополнения Иллюстрации/приложения: 11 шт.		Ваша оценка:
Аннотация: Приведены дополнения и анимации к статье "Решение Парадокса Эренфеста", опубликованной в журнале "Точная наука",

Путенихин Петр Васильевич : другие произведения.

Решение парадокса Эренфеста, дополнения